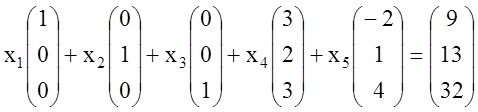Линейное программирование: Рабочая программа, контрольные работы и учебное пособие, страница 4

, (1.22)

или

,

где  – обозначения соответствующих вектор-столбцов в составе (1.22). Система векторов , , , ,  содержит три единичных вектора , , . Поэтому, следуя пункту 1.7.1, объявляем переменные , ,  базисными, а ,  – свободными и соответственно полагаем , . Тогда из (1.21) [или из (1.22)] получаем: , , . Вектор  будет искомым начальным опорным планом.

Целевая функция  достигает на нем значения

.

Ответ: начальный опорный план .

Выясним теперь: можно ли улучшить полученный план  и если можно, то как перейти к новому опорному плану. Сначала получим ответ на вторую часть вопроса, а именно: установим условия, при которых можно сформировать другой опорный план (не обязательно лучший).

1.7.2. Переход от начального опорного плана к новому

Всякий опорный план задачи (1.18), (1.19), равно как и задачи (1.20), (1.21), должен иметь три неотрицательные координаты и две – нулевые. Причем неотрицательным координатам должны отвечать векторы , образующие единичный базис, т.е. векторы, у которых одна координата равна единице, а остальные – нулю.

Допустим, что векторы , ,  линейно независимы и, значит, также образуют базис в системе векторов , , , , . Этот базис, в отличие от базиса , не будет в общем случае единичным, поскольку .

Сделанное предположение означает, что мы перешли от базиса  к новому , введя в старый базис вектор  вместо .

Если , ,  – новый базис, то переменные  – базисные, а ,  – свободные и, как следствие, , .

Система уравнений (1.19) в этом случае примет вид

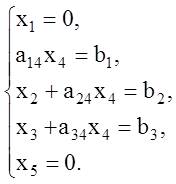                                (1.23)

Если , то СЛАУ (1.23) имеет единственное решение:

; ; ; ; .

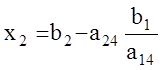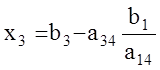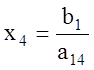Полученный вектор

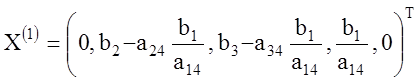               (1.24)

будет опорным планом, если его координаты  неотрицательны, т.е.

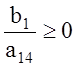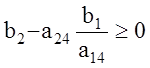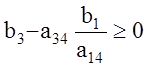,  ,  .               (1.25)

Поскольку , , то из первого неравенства 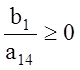 следует, что коэффициент  должен быть положительным ().

Если  и , то второе и третье неравенства в (1.25) будут выполняться.

Если же  и (или) , то должны выполняться неравенства

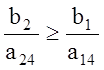 и (или) 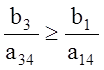.                         (1.26)

Если в соответствие СЛАУ (1.19) поставить ее расширенную матрицу

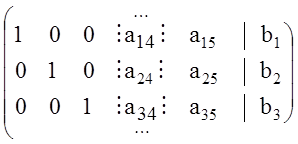,                     (1.27)

то неравенства (1.26) будут означать, что частное от деления элементов ,  столбца свободных членов СЛАУ на соответствующие элементы четвертого столбца ( или ) должно быть не меньше, чем частное от деления  на . Четвертый столбец в расширенной матрице (1.27) выделен «рамочкой».

Проведенный анализ позволяет сделать следующие выводы.

1. Вектор

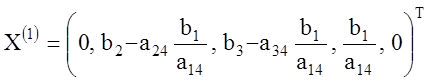
будет новым опорным планом, если координаты введенного в базис вектора  удовлетворяют условию

 (при условии, что выводится )

и при этом либо

, ,

либо

 и (или) ,

но выполняются неравенства (1.26).

2. Если две или более координаты вводимого в базис вектора  положительны (,,), то из неравенств (1.26) следует, что из старого базиса  нужно вывести тот вектор , которому отвечает наименьшее значение отношения 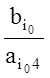, т.е., например,

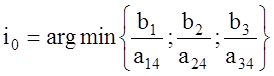,                         (1.28)

если ,,, и

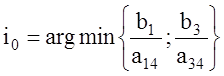,                                   (1.29)

если ,,.

3. В старый базис  можно ввести только тот вектор из совокупности векторов , у которого есть хотя бы одна положительная координата.

Покажем применение полученных выводов на примере 1.4, продолжив его решение.

Пример 1.4 (продолжение решения)

2. Выбор нового опорного плана

Запишем расширенную матрицу СЛАУ (1.21)

.

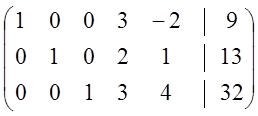В небазисных четвертом и пятом столбцах есть положительные элементы. Это означает, что в базис  можно ввести как вектор , так и вектор .

У вектора  все координаты положительны, поэтому, в соответствии с (1.28), находим номер вектора старого базиса, который нужно будет вывести, если в базис будет вводиться вектор :

.

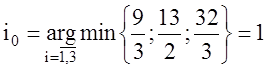Это означает, что если в старый базис будет вводиться вектор , то вывести из базиса нужно вектор . В этом случае ( – новый базис) полагаем ,  в СЛАУ (1.21) и получаем

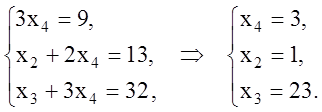
Отсюда  – новый опорный план, а  – новое значение целевой функции.

Вектор  имеет две положительные координаты, поэтому в соответствии с (1.29)

.

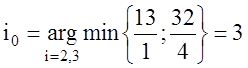Здесь  – номер строки, в которой стоят элементы  и  расширенной матрицы. Отсюда следует, что вектор  можно ввести вместо вектора .

Поскольку  – новый альтернативный базис, то  и  –свободные переменные. Полагая , , получаем из (1.21) СЛАУ и ее решение

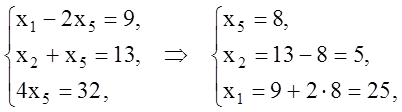
откуда  – альтернативный  новый план, а  – значение целевой функции на втором новом опорном плане. Отметим, что план  лучше, чем , так как .

Ответ: новые опорные планы  и .

1.7.3. Сравнение опорных планов

Рассмотренный в п.1.7.2 второй этап решения примера 1.4 показал, что даже в этом частном случае (, ) нахождение всех новых опорных планов в явном виде является достаточно трудоемкой задачей, поскольку требует решения  СЛАУ с  неизвестными. Максимальное число  возможных новых опорных планов в общем случае равно ; в примере 1.4 .

Оказывается, что можно не находить явно все новые опорные планы, а оценивать возможное уменьшение (увеличение) целевой функции косвенно в рамках специальных процедур.

Выясним условия, при которых новый опорный план  (1.24) будет лучше старого , т.е.  или .

Имеем

,

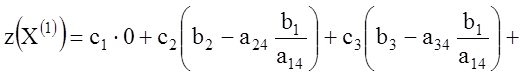
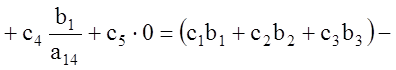
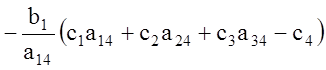но

и потому

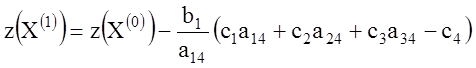
или

.

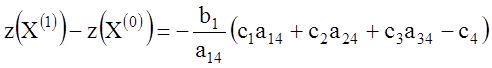Обозначим , тогда

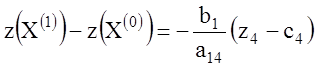.                  (1.30)

Поскольку 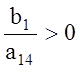, то искомое неравенство

будет иметь место, если будет выполняться неравенство

.                             (1.31)

Таким образом, введение в старый базис  вектора  вместо вектора , эквивалентное переходу от одной точки  многогранника допустимых решений к другой , приведет к уменьшению значения целевой функции, если будет выполняться неравенство (1.31). Разумеется, что аналогичное неравенство

                              (1.32)

должно выполняться и для любого другого вектора , вводимого в старый базис.

Обратим внимание на то, что величина

есть скалярное произведение вектора  на вектор . Поэтому если к расширенной матрице (1.27) приписать слева еще столбец C, а снизу приписать строку , то все вычисления можно проводить на этой матрице.

Так, в условиях примера (1.4) эта матрица имела бы следующий вид:

.           (1.33)

Покажем как вычисляются  и :