Линейное программирование: Рабочая программа, контрольные работы и учебное пособие, страница 6

Приведем без доказательства теоремы о числе решений задачи ЛП.

Теорема 1.8 (признак единственности оптимального плана). Задача ЛП (1.15), (1.16) имеет единственный оптимальный план, если  для любого вектора , не входящего в базис.

Теорема 1.9 (признак существования бесконечного числа оптимальных планов). Задача ЛП (1.15), (1.16) имеет бесконечное число оптимальных планов, если  хотя бы для одного вектора условий , не входящего в базис.

Теорема 1.10 (признак отсутствия оптимального плана).

Задача ЛП (1.15), (1.16) не имеет оптимального плана в силу неограниченности целевой функции на допустимом множестве, если для какого-либо вектора условий  с оценкой , не удовлетворяющей условиям оптимальности, среди его координат , , нет положительных, т.е. в задаче на минимум существует вектор  такой, что  и  ; в задаче на максимум существует вектор  такой, что  и  .

1.9. Алгоритм симплекс-метода

Алгоритм

1. Привести задачу ЛП к каноническому виду.

2. Найти начальный опорный план  с единичным базисом. Если система уравнений связи (1.16) не имеет единичного базиса, то привести ее к виду (1.37) с единичным базисом. Если начальный опорный план отсутствует, то задача не имеет решения (из-за несовместности системы ограничений).

3. Составить первоначальную симплекс-таблицу (табл. 1.2).

Таблица 1.2

Номера базисных векторов					…
					…
					…
…	…	…	…	…	…	…
					…
					…
					…

4. Проверяем условия оптимальности (теоремы 1.6 – 1.10).

Если условия оптимальности выполняются, то  – оптимальный план; если не выполняются, то переходим к другому опорному плану . Для этого находим разрешающий элемент – элемент , индексы  и  которого определяют номера соответственно выводимого из базиса вектора  и вводимого вместо него .

5. Выбор разрешающего столбца (номера вводимого в базис вектора):

а) если в строке оценок  (последняя строка симплекс-таблицы) оценка  не удовлетворяет условию оптимальности ( в задаче на минимум и  в задаче на максимум), то  – искомый номер столбца.

б) если в строке оценок  несколько оценок не удовлетворяют условию оптимальности, например , , …, , , то находим

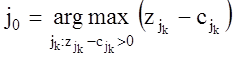 (в задаче на минимум),

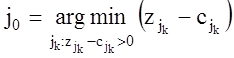 (в задаче на максимум).

Тогда  – номер разрешающего столбца.

6. Выбор разрешающей строки (номера вектора, который выводится из базиса):

а) если в выбранном разрешающем столбце  имеется единственный положительный элемент , то  – искомый номер разрешающей строки, а  – разрешающий элемент;

б) если в -м столбце более одного положительного элемента, т.е. ,…,, , то

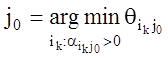,    где    .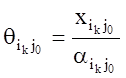

Тогда  – номер разрешающей строки, а  – разрешающий элемент, с помощью которого строится новая симплекс-таблица.

7. Построение новой таблицы.

В первом столбце таблицы число  заменяется числом . В третьем столбце координата  вектора  заменяется числом . Все элементы разрешающей -й строки начиная с четвертого столбца делятся на разрешающий элемент , т.е. заменяются числами , .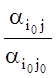

В результате этой операции в разрешающем столбце на месте разрешающего элемента получится 1. Затем с помощью элементарных преобразований над строками таблицы получаем нули в разрешающем столбце на месте всех остальных элементов. Этим преобразованиям отвечают вычисления новых значений элементов таблицы по так называемому правилу прямоугольников

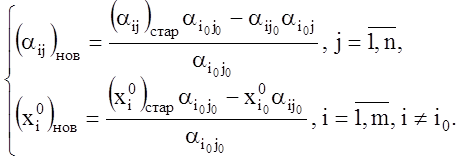     (1.42)

8. Проверка оптимальности нового плана.

По формулам (1.40) и (1.41) вычисляются величины  и , . Затем проводится анализ построенной симплекс-таблицы в соответствии с критериями, зафиксированными в теоремах 1.6 – 1.10.

Пример 1.5. Решить задачу ЛП.

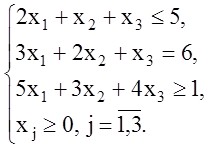
Решение. В системе ограничений задачи два неравенства. Для приведения задачи к каноническому виду вводим вспомогательные неотрицательные переменные  и , соответственно прибавляя  к левой части первого неравенства и вычитая  из левой части третьего неравенства в системе ограничений. Получим задачу

     (1.43)

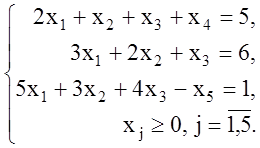                    (1.44)

Для построения единичного базиса и начального опорного плана приведем систему ограничений (1.44) методом Гаусса-Жордана к равносильной разрешенной форме

.

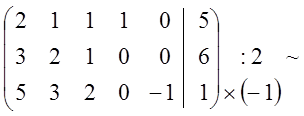
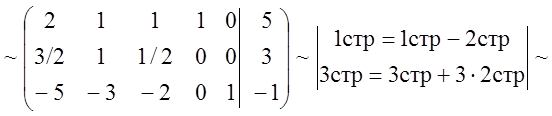
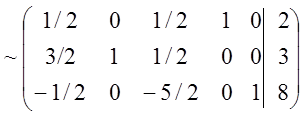Полученная равносильная система уравнений связи

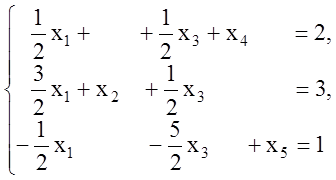
содержит единичный базис .

Составим первую симплекс-таблицу (табл. 1.3).

Таблица 1.3

			¯5	2	-1	0	0
4	2	0		0		1	0	4
2	3	2		1		0	0	2
5	8	0		0		0	1
		6	3	2	1	0	0
			-2	0	2	0	0

Вычисляем значения , , , по формуле (1.40). Это эквивалентно вычислению скалярных произведений , , …, . Так, например,

,

,

,

………………………………

.

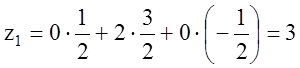Эти результаты заносятся в предпоследнюю строку таблицы. В последней строке таблицы содержатся значения :

,         ,           ,

,           .

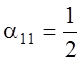Построенный начальный опорный план  доставляет целевой функции значение . Оно не является оптимальным, поскольку среди  есть отрицательное значение  (теорема 1.7), а в столбце координат вектора  есть положительные величины  и .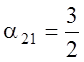

Найдем теперь номер  разрешающей строки и разрешающий элемент . В соответствии с пунктом 6,б, алгоритма, приведённого в разделе 1.9, вычисляем

,    .

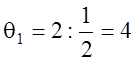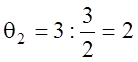Поскольку , то  и 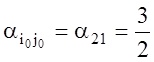. Это означает, что в базис нужно ввести вектор , а вывести .