Определим теперь скорость
распространения сигнала по возбудимому нервному волокну. Для этого необходимо
положить, что при Q = 0
потенциал мембраны имеет пороговое значение ![]() ,
т.е. в левой части (29) необходимо вместо А1 записать
,
т.е. в левой части (29) необходимо вместо А1 записать ![]() .
.
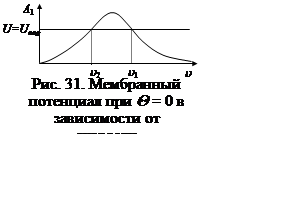 Правая часть (29) представляет
собой функцию e (а, значит, и u). Эта функция для тока возбуждения в
виде двуполярного прямоугольного импульса (рис. 28) носит экстремальный характер
(рис. 31): она равна нулю при u
= 0 и стремится к нему при u ® ¥.
Модель тока, соответствующая рис. 30, приводит для А1 к
соотношению (29), из которого также следует А1® 0 при u
® ¥.
Достичь условия А1 = 0 при u
= 0 можно подбором коэффициентов a,
b, I01,
I02. При этом связь между ними дается
соотношением:
Правая часть (29) представляет
собой функцию e (а, значит, и u). Эта функция для тока возбуждения в
виде двуполярного прямоугольного импульса (рис. 28) носит экстремальный характер
(рис. 31): она равна нулю при u
= 0 и стремится к нему при u ® ¥.
Модель тока, соответствующая рис. 30, приводит для А1 к
соотношению (29), из которого также следует А1® 0 при u
® ¥.
Достичь условия А1 = 0 при u
= 0 можно подбором коэффициентов a,
b, I01,
I02. При этом связь между ними дается
соотношением:
![]() .
(31)
.
(31)
Таким образом, можно добиться соответствия характера
поведения функции (29) функции, изображенной на рис. 31. Из последнего следует,
что заданному значению порогового напряжения соответствуют две скорости.
Значение первой (u1)
может быть получено из условий e >>a, e >> b. В этом случае, пренебрегая вторым и третьим слагаемыми в
коэффициентах перед I01 и I02, приходим к соотношению 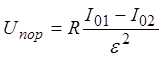 , подставив в которое значение e, получаем окончательно:
, подставив в которое значение e, получаем окончательно:
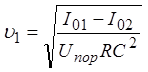 . (32)
. (32)
Разность I01 – I02 – амплитуда тока возбуждения при Q = 0.
Второе
значение скорости определяется из противоположного соотношения между e и a, b. В этом
случае, пренебрегая членами, содержащими ![]() ,
приходим к выражению
,
приходим к выражению
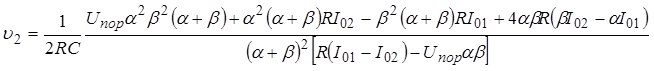 которое
с учетом (31) преобразуется к виду:
которое
с учетом (31) преобразуется к виду:
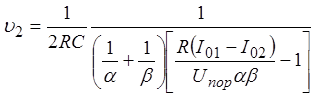 .
.
Используя
(32), свяжем ![]() и
и ![]()
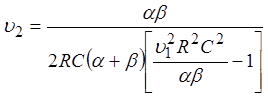 .
.
Учитывая ![]() , а также e 1>>a, e 1 >> b,
последнюю формулу можно упростить:
, а также e 1>>a, e 1 >> b,
последнюю формулу можно упростить:
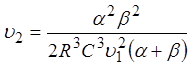 .
.
Отношение ![]() определится соотношением:
определится соотношением:
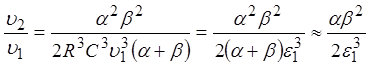 ,
,
из которого
следует ![]() .
.
Анализируя выражение для
потенциала в правой полуплоскости UI,
можно сделать вывод, что абсолютное значение производной dUI /dQ для сигнала, движущегося со
скоростью ![]() , равное e 1, значительно превосходит абсолютное значение
производной для сигнала, движущегося со скоростью
, равное e 1, значительно превосходит абсолютное значение
производной для сигнала, движущегося со скоростью ![]() ,
равное e 2, т.е.
фронт напряжения сигнала, движущегося с большей скоростью, значительно более
крут, чем фронт напряжения сигнала, движущегося с меньшей скоростью.
,
равное e 2, т.е.
фронт напряжения сигнала, движущегося с большей скоростью, значительно более
крут, чем фронт напряжения сигнала, движущегося с меньшей скоростью.
Оценим теперь соотношение
максимальных значений напряжений для сигналов, движущихся со скоростями ![]() и
и ![]() .
Разложив функцию для потенциала в левой полуплоскости в ряд Тейлора и удерживая
лишь члены первого порядка, приходим к выражению:
.
Разложив функцию для потенциала в левой полуплоскости в ряд Тейлора и удерживая
лишь члены первого порядка, приходим к выражению:
![]() ,
,
первая
скобка в котором представляет собой коэффициент А1, т.е. ![]() , а вторая – (–eА1), т.е. (–e
, а вторая – (–eА1), т.е. (–e![]() ).
Следовательно,
).
Следовательно, ![]() .
.
Участок эквивалентной линии заряжается до максимального напряжения к моменту окончания отрицательной фазы импульса тока возбуждения. Этот момент можно оценить как величину, обратную постоянной затухания a, характеризующей отрицательный импульс. Тогда максимальное напряжение сигнала, движущегося с большой скоростью, U121 будет равно
![]() ,
,
а максимальное напряжение сигнала, движущегося с малой скоростью, U122 –
![]() .
.
Из e1 >> a, а e2
<< a следует, что
максимальное напряжение в сигнале, движущемся с большой скоростью, значительно
превосходит пороговое напряжение, а в сигнале, движущемся с малой скоростью,
имеет порядок ![]() . Величины e1 и e2 являются постоянными затухания
напряжения в правой полуплоскости, и, следовательно, из e1 >> e2 следует, что сигнал с
большой скоростью значительно более сосредоточен в пространстве, чем сигнал с
малой.
. Величины e1 и e2 являются постоянными затухания
напряжения в правой полуплоскости, и, следовательно, из e1 >> e2 следует, что сигнал с
большой скоростью значительно более сосредоточен в пространстве, чем сигнал с
малой.
Рассмотрим вопрос об
устойчивости скоростей распространения. Из рис. 31 видно, что при случайном
увеличении скорости быстрого импульса потенциал его передней части становится
меньше порогового, условия возбуждения перестают выполняться, скорость распространения
импульса замедляется, т.е. возвращается в исходную точку. При уменьшении
скорости происходит обратное. В случае медленного сигнала случайное увеличение
скорости приводит к дальнейшему ее росту и переходу из точки ![]() к точке
к точке ![]() .
Замедление же импульса приводит к уменьшению потенциала ниже порогового уровня
и прекращению распространения. Это напоминает процесс тления: при увеличении
температуры тлеющего участка он начинает гореть, при уменьшении – затухает.
.
Замедление же импульса приводит к уменьшению потенциала ниже порогового уровня
и прекращению распространения. Это напоминает процесс тления: при увеличении
температуры тлеющего участка он начинает гореть, при уменьшении – затухает.
Таким образом, точка ![]() является устойчивой, а
является устойчивой, а ![]() - нет. Отметим также, что
зависимость скорости распространения от диаметра волокна в случае возбудимых
волокон такая же, как и в случае невозбудимых. Она пропорциональна квадратному
корню диаметра. В самом деле, I0 ~ b, R ~ 1/b2, C ~ b
и, значит,
- нет. Отметим также, что
зависимость скорости распространения от диаметра волокна в случае возбудимых
волокон такая же, как и в случае невозбудимых. Она пропорциональна квадратному
корню диаметра. В самом деле, I0 ~ b, R ~ 1/b2, C ~ b
и, значит, ![]() .
.
Оценим теперь численное значение скорости распространения сигнала в возбудимых волокнах. В качестве примера рассмотрим аксон кальмара со следующими параметрами:
I01
– I02 = 6,3×10-3 А/м, ![]() = 18,5×10-3 В,
= 18,5×10-3 В,
С = 15,7×10-6 Ф/м, R = 2,5×106 Ом/м, b = 5×10-4 м.
Подстановка их в (32) дает u » 23,4 м/с, что неплохо совпадает с экспериментальным значением u » 21,2 м/с.
Учтем приближенно
конечную проводимость мембраны, полагая, что вклад этой проводимости в решение
уравнения для возбудимого волокна является возмущающим фактором. Решение
уравнения (26) в этом предположении можно записать в виде ![]() , где
, где ![]() -
решение, учитывающее несовершенство мембраны,
-
решение, учитывающее несовершенство мембраны, ![]() -
решение уравнения без учета потерь в мембране,
-
решение уравнения без учета потерь в мембране, ![]() -
составляющая, отражающая влияние потерь. Подставим
-
составляющая, отражающая влияние потерь. Подставим ![]() в
(26), преобразовав его с учетом обозначений
в
(26), преобразовав его с учетом обозначений ![]() ,
, ![]() :
:
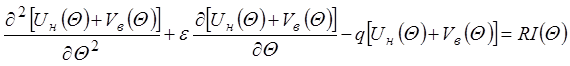 .
.
Будем
полагать, что решение ![]() удовлетворяет дифференциальному
уравнению для невозмущенного случая:
удовлетворяет дифференциальному
уравнению для невозмущенного случая:
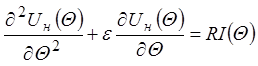 .
.
Учитывая ![]() , пренебрежем в члене, содержащем q, функцией
, пренебрежем в члене, содержащем q, функцией ![]() . Тогда
дифференциальное уравнение для нахождения возмущающей функции приобретет вид:
. Тогда
дифференциальное уравнение для нахождения возмущающей функции приобретет вид:
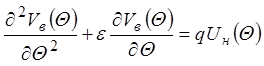 .
.
Зависимость ![]() известна. Она определяется функцией
известна. Она определяется функцией ![]() . Для упрощения решения
аппроксимируем
. Для упрощения решения
аппроксимируем ![]() степенной функцией и
запишем
степенной функцией и
запишем ![]() в виде:
в виде: ![]() .
Расчет показывает, что
.
Расчет показывает, что ![]() в области
в области ![]() достаточно хорошо аппроксимируется
параболой, симметричной относительно
достаточно хорошо аппроксимируется
параболой, симметричной относительно ![]() =-0,7 см и
пересекающей ось абсцисс в точках
=-0,7 см и
пересекающей ось абсцисс в точках ![]() =0 и
=0 и ![]() =-1,4 см. Функция в максимуме
=-1,4 см. Функция в максимуме ![]() и коэффициенты К1,
К2, К3 при этом приобретают значения:
и коэффициенты К1,
К2, К3 при этом приобретают значения:
![]() =120
mB; К1 =-192 mB/см2;
К2 = -276 mB/см; К3
= 0.
=120
mB; К1 =-192 mB/см2;
К2 = -276 mB/см; К3
= 0.
Подстановка ![]() в правую часть уравнения для
в правую часть уравнения для ![]() приводит к решению:
приводит к решению:
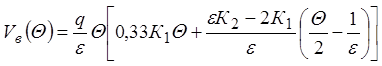 ,
,
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.