-.201E-04 -.775E-05 .656E-03
.193E-03 .115E-03 -.114E-03 .448E-03
-.430E-02 -.145E-02 -.567E-03 -.227E-02 .373E-01
ОЦЕНКИ КОЭФФИЦИЕНТОВ .41768 .31047 .48285 .53804 .17763
Т.о.
![]()
Значение множественного коэффициента корреляции 0.994, следовательно, полученную регрессионную модель можно считать достаточно точной.
Одной из ключевых проблем при проектировании АИУС является проблема оптимизации, от обоснованной постановки и успешного решения которой во многом зависит эффективность АИУС. Решение проблемы оптимизации предполагает решение двух взаимосвязанных задач, а именно, математическую формулировку задачи оптимизации и выбор метода ее решения. На практике постановка задачи оптимизации - наименее формализованный и наиболее ответственный этап, когда на основе тщательного анализа объекта необходимо выяснить основную цель производства, уточнить ограничения задачи, определить характер имеющейся об объекте информации и с учетом всех данных перейти от вербального (словесного) описания задачи к ее математической формулировке.
В качестве вектора переменных, оптимальные значения
которых подлежат вычислению в процессе решения задачи оптимизации (плана задачи)
выберем вектор управляемых переменных ![]() .
.
В качестве критерия оптимизации (целевой функции) выберем паропроизводительность парогенератора Y1, т. к. ее увеличение ведет к повышению экономической рентабельности эксплуатации ТОУ:
![]()
Т.к. управляемые переменные можно изменять в ограниченных пределах, что связано с требованием нахождения в рабочей области, то в задаче будут действовать следующие ограничения:
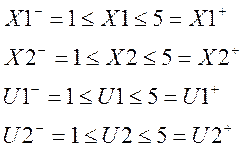
Так же необходимо учитывать существование следующей связи в объекте (функционального ограничения):
![]()
Т.к. превышения пороговых значений Y2
приводит к существенным потерям, то по технологическим соображениям задачу стохастическая
задача нахождения оптимального технологического режима ![]() может быть сформулирована в виде
задачи оптимизации по вероятности (Р - модель):
может быть сформулирована в виде
задачи оптимизации по вероятности (Р - модель):
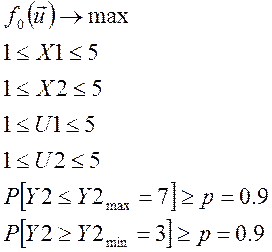
1. Произведем искусственное сведение стохастической задачи к детерминированной:
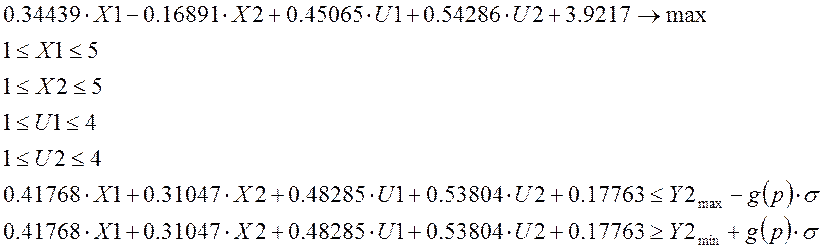
где
![]() - квантиль нормированного
нормального распределения для заданной вероятности
- квантиль нормированного
нормального распределения для заданной вероятности ![]() .
.
Т.о. задача приобретает вид:
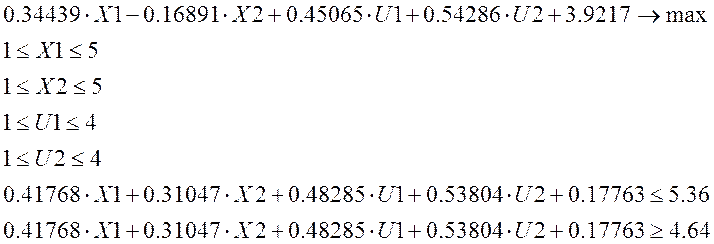
Оптимальный
план поставленной задачи: ![]()
![]()
2. Произведем исследование чувствительности полученного оптимального решения к ошибкам в определении коэффициентов.
Пусть коэффициенты в регрессионных моделях меняются в некоторых ограниченных пределах, т. е.
![]()
где
![]() и
и ![]() —
заданные векторы.
—
заданные векторы.
Для определения пределов изменения критерия
оптимизации необходимо решить две задачи: одну с «широкой» допустимой областью
и критерием, коэффициенты которого равны своим нижним предельным значениям ![]() ,
другую — с «узкой» допустимой областью и критерием с коэффициентами
,
другую — с «узкой» допустимой областью и критерием с коэффициентами ![]() и для каждой из этих задач рассчитать оптимальное
значение критерия Y1. Тогда при любых коэффициентах
и для каждой из этих задач рассчитать оптимальное
значение критерия Y1. Тогда при любых коэффициентах ![]() ,
лежащих в указанных пределах, критерий оптимизации будет лежать между этими
крайними значениями.
,
лежащих в указанных пределах, критерий оптимизации будет лежать между этими
крайними значениями.
Для «широкой» допустимой области задача имеет вид:
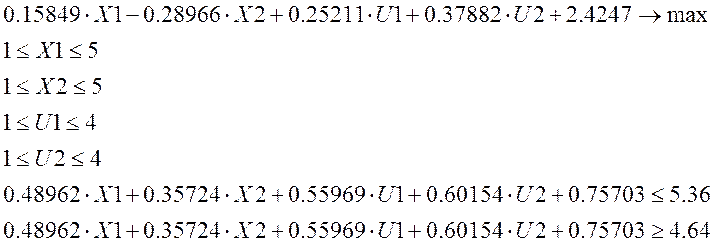
Оптимальный
план поставленной задачи: ![]()
![]() .
.
Для «узкой» допустимой области задача имеет вид:
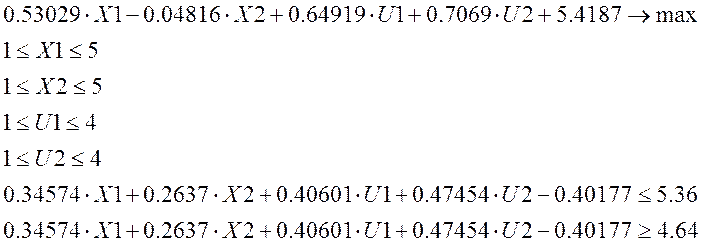
Оптимальный
план поставленной задачи: ![]()
![]() .
.
Т.о. при любых коэффициентах в регрессионной модели, лежащих в указанных пределах критерий оптимизации будет лежать между крайними значениями:
![]()
Ошибки в определении коэффициентов могут вносить существенные коррективы в оптимальный план задачи.
3. Решим поставленную задачу, основываясь на испытании следующих статистических гипотез:
![]()
Для любого фиксированного вектора ![]() можно найти предсказанное значение
можно найти предсказанное значение ![]() и определить дисперсию этого
предсказания
и определить дисперсию этого
предсказания ![]() , где
, где ![]() - ковариационная матрица
коэффициентов регрессионной модели. Допустимая область задачи, основанная на
критерии для проверки гипотезы
- ковариационная матрица
коэффициентов регрессионной модели. Допустимая область задачи, основанная на
критерии для проверки гипотезы ![]() при
заданной вероятности
при
заданной вероятности ![]() (вероятность
отвергнуть верную гипотезу) имеет вид:
(вероятность
отвергнуть верную гипотезу) имеет вид:
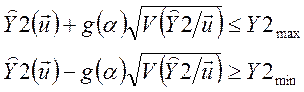
Если
имеются два допустимых решения ![]() и
и ![]() , то целесообразно считать вектор
, то целесообразно считать вектор ![]() «лучше»
«лучше» ![]() в
смысле критерия оптимизации, если вектору
в
смысле критерия оптимизации, если вектору ![]() соответствует
меньшее значение порога критерия оптимизации:
соответствует
меньшее значение порога критерия оптимизации:
![]()
Т.о. задачу оптимизации можно записать в виде:
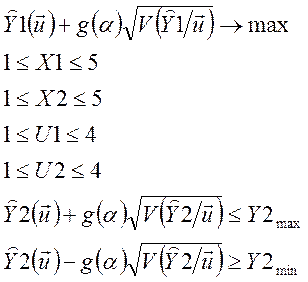
Окончательно задача приобретает вид:
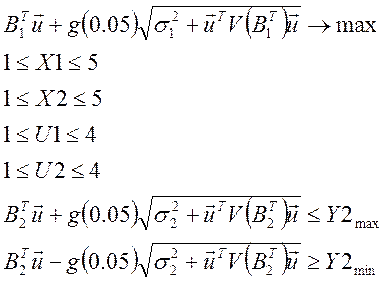
Оптимальный
план поставленной задачи: ![]()
![]() .
.
Идентификация динамических параметров по данным измерений невозможна, если в измерениях отсутствуют переходные процессы. Поэтому ни один метод не позволяет провести динамическую идентификацию по данным об установившемся состоянии. Методы идентификации динамических характеристик объектов управления, которые впервые были реализованы в системах управления, основаны на использовании частотных, ступенчатых и импульсных воздействий. Большинство этих методов применяются для линейных процессов, однако их можно использовать и в линеаризованных системах, если уровни сигналов невелики. Наиболее исследована задача параметрической идентификации, когда структура объекта известна с точностью до параметров, которые либо неизвестны, либо изменяются с течением времени неизвестным (в общем случае случайным) образом.
Для получения разгонной характеристики поставим следующий эксперимент: подвергнем ТОУ скачкообразному входному воздействию по переменной U2 и зафиксируем картину переходного процесса (данные peregrev.i16):
|
|
|
Рис. 54. График зависимости выходной величины Y3 от времени при скачкообразном изменении входной величины U2 |
Аналитический
вид передаточной функции: 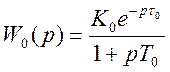
Определим неизвестные параметры:
Установившиеся значения:
U2 = 4.56
Y3 = 5.12
Коэффициент передачи K0 = 1.12
Графоаналитическим методом определяем:
время запаздывания t0 = 17 c
постоянная времени T0= 15 c
Полученная
передаточная функция ТОУ: 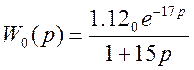
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.