Электромагнитные переходные процессы в электрических системах: Сборник задач для студентов электроэнергетических специальностей, страница 8

i_2/0/= i′_2/0/ + i″_2/0/ = A₂e⁰ ,

здесь i′_2/0/ = 0.

Отсюда:

A₂ = i_msin (α – φ) .

Определение  полного тока.

      Полный ток в цепи с параметрами X₁,R₁ после замыкания контакта:

i₁(t) = i′(t) + i″(t) = I_1msin (ωt + α – φ₁) + [I_msin (α – φ) – I_1msin (α – φ₁)]e ^p1t

В расчетах вместо индуктивности Lиспользуют X = ωL, а вместо корня характеристического уравнения p − постоянную времени затухания апериодической составляющей T_a = 1/p и последнее выражение записывают в виде:

i₁(t) = i′₁(t) + i″₁(t) = I_1msin (ωt + α – φ₁) + [I_msin (α – φ) –

I_1msin (α – φ₁)]e^{-t/ Ta1}.

Полный ток в цепи с параметрами X₂,R₂ после замыкания контакта:

i₂(t) = i′₂(t) + i″₂(t) = [I_msin (α – φ)]e^{-t/ Ta2}.

Из двух последних выражений видно, что начальное значение апериодической составляющей зависит от амплитуд токов и момента коммутации, то есть от так называемой фазы включения (угла включения) α, а также от угла между током и напряжением как до, так и после коммутации (φ, φ₁).

2.1.2. Решение задачи операторным методом.

В этом случае также требуется первоначально составить дифференциальные уравнения в соответствии с первым и вторым законами Кирхгофа. Затем следует перейти от дифференциальных уравнений к операторным или, иначе говоря, от оригиналов функций f(t) к их изображениям F(p). Переход возможен на основе интегрального преобразования или с применением таблиц соответствия. К преимуществам операторного метода относят замену решения системы дифференциальных уравнений для оригиналов решением алгебраических уравнений для изображений и упрощение учета начальных условий [5]. На последнем этапе расчета выполняется переход от изображений к оригиналам, что возможно на основе таблиц соответствия или теоремы разложения.

При решении задач операторным методом можно составлять уравнения для изображений искомых величин, минуя этап составления дифференциальных уравнений [6]. В этом случае законы Кирхгофа в операторной форме  в общем случае записываются в виде:

,

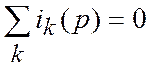
(2.3)

где 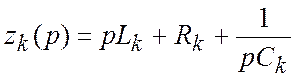- операторное сопротивление ветви.

Такая запись применена при решении задачи операторным методом в главе 3.

Вид исходных дифференциальных уравнений (2.1), (2.2) не меняется.

Выполним переход от оригиналов к изображениям.

Запишем для участка с параметрами X₁,R₁ уравнение в операторной форме:

В наиболее общем виде [6] уравнение контура с параметрами R,L,C в операторной форме:

U(p) = (pL + R + 1/pC)i(p) – Li(0_-) + U_C(0_-) /p,

 Участок с параметрами X₁,R₁ в соответствии с принятыми допущениями не содержит емкости, поэтому:

U(p) = (pL₁ + R₁)i₁(p) – L₁i₁(0_-),

где i₁(0_-) - ток в контуре в момент t= 0_- .

Можно составить для участка с параметрами X₁,R₁ уравнение в операторной форме на основе соотношения (2.3). При этом вид последней записи не изменится.

Отсюда:

i₁(p) = [U(p) + L₁i₁(0_-)]/ (pL₁ + R₁).

Синусоидальной функции U_msin (ωt + α) соответствует изображение U(p) = U_m [(psinα +  ωcosα)/(p² + ω²)], операторное выражение для напряжения достаточно громоздко, последующие расчетные выражения будут сложны. Целесообразно воспользоваться комплексным представлением напряжения источника U_msin(ωt + α) = Im{Ue^jωt}, то есть изменяющееся по закону синуса напряжение источника может быть представлено как проекция вектора U_m на мнимую ось, как мнимая часть комплекса Ue^jωt. Изображение экспоненциального напряжения достаточно просто [5]: Ue^jωt ~ U/(p – jω). Таким образом:

i₁(p) ={ [U/(p – jω)] + L₁i₁(0_-)]}/ (pL₁ + R₁).

Для участка цепи с параметрами X₂,R₂ после замыкания контакта уравнение в операторной форме:

0 = (pL₂ + R₂)i₂(p) – Li₂(0_-).

Отсюда:

i₂(p) = [L₂i₂(0_-)]/ (pL₂ + R₂).

Для получения ответа выполним переход от изображений к оригиналам.

Рассмотрим участок с параметрами X₁,R₁, введем параметр b₁ = R₁/ L₁, разделим числитель и знаменатель выражения для i₁(p) на L₁, получим в области изображений:

i₁(p) ={ [(U/ L₁)/ (p – jω)] + i₁(0_-)]}/ (p + b₁).

В силу принципа линейности сложение оригиналов соответствует сложению изображений, умножение оригиналов соответствует умножению  изображений [2]. В последнем выражении содержится два слагаемых. По таблице соответствий находим оригинал первого слагаемого:

f₁(t) = [(U/ L₁)/ (b₁ + jω)]( e ^jωt -  e ^-b1t ).

Выделим мнимую часть последнего выражения, запишем последовательно:

(U/ L₁)/ (b₁ + jω) = U/ (R₁ + jωL₁) = (U_m/ Z₁)e ^{j(α -φ1)},

где: Z₁ = √[R₁²+(ωL₁)²], φ₁ = arctg(X₁/R₁);

f₁(t) = (U_m/Z₁)e^j(α-φ1)(e^jωt-e^-b1t),

искомый ток по первому слагаемому определим как  проекцию вектора f₁(t) на мнимую ось:

i₁₁(t) = Jm{f₁(t)} = (U_m/ Z₁)[sin(ωt + α – φ₁)– sin (α – φ₁) e ^{- t / Ta1t}].

По таблице соответствий находим оригинал второго слагаемого:

i₁₂(t) =  i₁(0_-) e ^-b1t_.

i₁(0_-) - ток в контуре в момент t = 0_-, то есть ток в контуре до коммутации, этот ток был определен в п. 2.1.1 при решении задачи классическим методом. С учетом обозначения T_a1 = X₁/ ωR₁ получаем:

i₁(t) = [i_msin (α – φ)]e ^{-t / Ta1}_.  

Полный ток участка с параметрами X₁,R₁ состоит из двух слагаемых: i₁₁(t), i₁₂(t):

i₁(t) = i₁₁(t)  + i₁₂(t) = (U_m/ Z₁)[sin(ωt + α – φ₁)– sin (α – φ₁) e ^{- t / Ta1t}] +

[i_msin (α – φ)] e ^{- t / Ta1t} =

i_1msin (ωt + α – φ₁) + [i_msin (α – φ) – i_1msin (α – φ₁)]e^{-t/ Ta1t}.

Этот результат совпадает с полученным ранее классическим методом результатом.

Рассмотрим участок с параметрами X₂,R₂, введем параметр b₂ = R₂/ L₂, разделим числитель и знаменатель выражения для i₂(p) на L₂, получим в области изображений:

i₂(p) = i₂(0_-)/ (p + b₂).

По таблице соответствий, приведенной, например в [2], находим оригинал:

i₂(t) = i₂(0_-) e ^-b2t_.

Здесь:  i₂(0_-) - ток в контуре в момент t = 0_-, то есть ток в контуре до коммутации, этот ток был определен в п.2.1.1.2 при решении задачи классическим методом. С учетом обозначения T_a2 = X₂/ ωR₂ получаем:

i₂(t) = I_msin (α – φ)] e ^{- t / Ta2t}   

2.1.3. Расчет процесса трехфазного КЗ численными методами.

Современные вычислительные средства позволяют получить численные решения составленных дифференциальных уравнений, это может быть сопряжено с разработкой или поиском программы для решения дифференциальных уравнений.