Входной сигнал может быть нечетким, заданным функцией принадлежности, или сама функция преобразования является нечеткой.
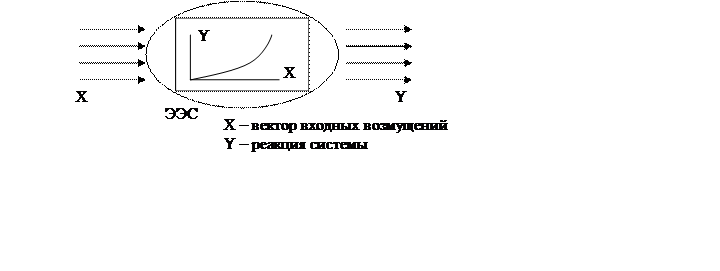

В принципе, нечеткие модели не обязательно являются чисто качественными. В некоторой степени они позволяют делать логические выводы, и поэтому область их применения расширяется.
Пример: Чем больше X, тем больше Y. X примерно равен Y.
На этом основании можно делать некоторые логические выводы, хотя они и не выражены численно. Такое умозаключение свидетельствует о том, что на основе субъективных рассуждений можно также делать продуктивные выводы.
1.7. Обсуждение результатов
Приведенные выше рассуждения позволяют сделать следующие заключения:
1. Природа реальной действительности такова, что не все переменные могут иметь своими значениями числа. Часть из них, а именно: лингвистические переменные; используют в качестве значений выраженные слова или предложения. При этом базовая переменная может опираться на числовые значения (например, возраст). Но часть из них может не иметь числовой шкалы (наружность, истинность).
2. Восприятие действительности осуществляется по двум генеральным линиям:
· объективная (объективизм: основан на левополушарном мышлении и требует полной информации, опирается на логические выводы и исходную аксиоматику, характеризует компьютерные вычисления и сам компьютер, также окружающую действительность) → объект (объективно существует);
· субъективная (опирается на правополушарное мышление (эвристику и интуицию), работает при неполной и даже противоречивой информации, что недопустимо для объективного восприятия, то есть построен на субъективизме) → субъект.
Сплав объективизма и субъективизма порождает создание человеко-машинных систем, и они удачно дополняют друг друга.
3. В настоящее время можно считать доказанным, что нечеткие представления и нечеткие выводы не размывают результат, как думает обыватель, а делают его более содержательным. Это обусловлено тем, что всякие детерминистические утверждения и результаты хотя и имеют численно строгий результат, в реальной действительности подвергаются случайным отклонениям и объективным восприятиям.
2. Теория четких множеств
2.1. Общие соображения
За 30 лет существования ТНМ в ней возникло несколько разных направлений. Однако все они опираются на общую теорию множеств, а в нашей терминологии – на теорию четких множеств. Несмотря на то, что в реальной действительности все множества имеют некоторые реально размытые границы, в первом приближении человечеством была разработана и освоена общая теория четких множеств, когда между множествами существуют четкие разграничения. Такие представления в настоящее время следует относить к консервативным и ограниченному восприятию действительности.
Существуют две теории четких множеств:
1. Аксиоматическая – требует высокого уровня абстракции и математической подготовки. Она отчасти является малопродуктивной и имеет эклектический характер.
2. Элементарная теория множеств – достаточна для понимания общей концепции теории множеств и получения объективных результатов. Широко применяется в инженерных, экономических и биологических науках. Ниже будем опираться на эту теорию.
2.2. Основные понятия и определения
Любая дисциплина вынужденно/преднамеренно устанавливает базовые понятия и определения, опираясь на которые, выстраивается вся теория. Некоторые из них выбираются аксиоматически, то есть являются конвенционными понятиями (определены на основе конвенции).
1) Множество – некоторая совокупность объектов, с которыми имеем дело и которые являются однородными и принадлежат одному классу.
Примечание: множества обозначаются большими заглавными буквами (A, B, C, D, …, Z).
2) Элементом множества называется один из объектов, принадлежащих этому множеству (a, b, c, d, …, z)
Пример: X = {x1, x2, x3, …, xi, …, xn}
![]() (для всех x,
принадлежащих X)
(для всех x,
принадлежащих X)
3) Количество элементов в множестве называется мощностью множества
Пример: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
A = {0, 2, 4, 6, 8} #=5
B = {1, 3, 5, 7, 9} #=5
C = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} #=10
Если #=1 – синглетон
Существуют следующие действия с множествами:
1. Включение
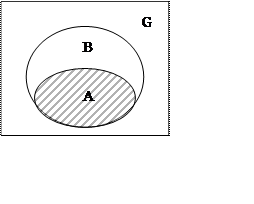
![]() (A влечет за собой B)
(A влечет за собой B)
2. Объединение
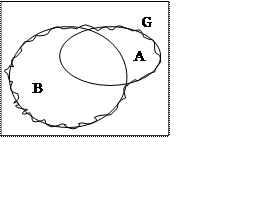
![]() ("ИЛИ")
("ИЛИ")
3. Пересечение
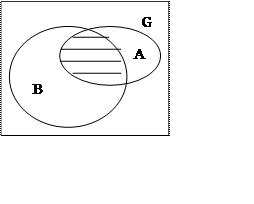
![]() ("И")
("И")
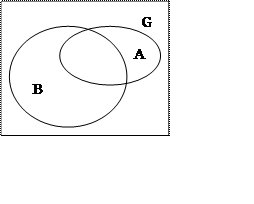
4. Дополнение
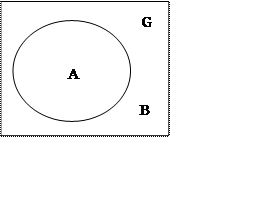
A + B = G
5. Отрицание
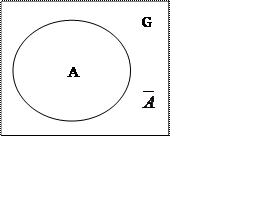
![]() ("НЕ")
("НЕ")
Двойное отрицание:
![]()
6. Включение
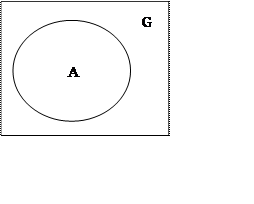
![]()
Это основные свойства четких множеств и логические связки, которые являются элементами естественного языка.
4) Если множество обладает одним свойством, то оно называется унарным. Если оно обладает двумя свойствами – бинарным.
2.3. Общие законы теории четких множеств
Рассмотрим общие законы теории четких множеств. В теории множеств существуют несколько законов, которые определяют алгебру четких множеств. По аналогии с этим далее будет рассматриваться алгебра нечетких множеств, что позволит провести сравнительный анализ.
1) Закон идемпотенции (идемпотентности)

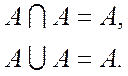
2) Закон коммутативности (перестановки, объединения)
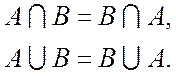
Замечание: Закон коммутативности не работает при умножении матриц.
3) Закон ассоциативности
![]() ,
,
![]() .
.
4) Закон абсорбции
![]() .
.
5) Закон дистрибутивности
![]() ,
,
![]() .
.
6) Закон комплементарности
![]() ,
,
![]() .
.
7) Закон двойного отрицания
![]() .
.
8) Законы де Моргана
![]() ,
,
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.