Пример.
1) Показать, что поле
вектора ![]() потенциально и найти его потенциал.
потенциально и найти его потенциал.
Решение.
Поле вектора ![]() будет потенциальным, если
будет потенциальным, если ![]() =0.
=0.
Найдем ![]() .
.
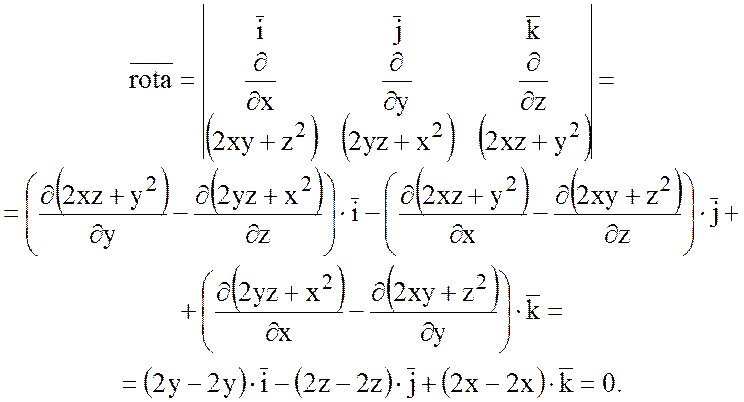
Так как ![]() =0, то поле вектора
=0, то поле вектора ![]() потенциально. Найдем потенциал. В
качестве точки
потенциально. Найдем потенциал. В
качестве точки ![]() возьмем (0;0;0).
возьмем (0;0;0).
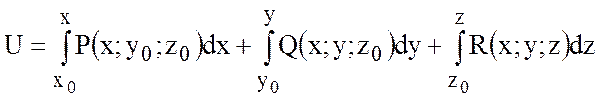 .
.
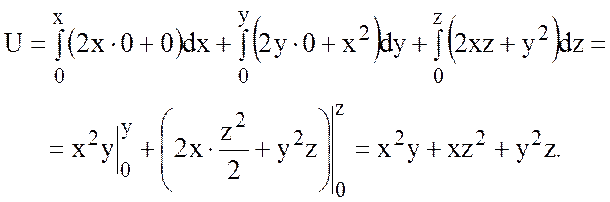
Можно проверить, что
функция U действительно является потенциалом
векторного поля вектора ![]() . Если U потенциал, то
. Если U потенциал, то  .
.
Найдем 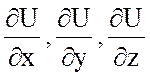 .
.
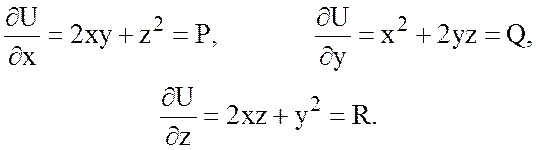
Ответ: ![]() .
.
2) Проверить, будет ли поле вектора
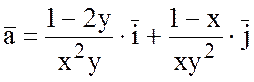 потенциальным
и найти его потенциал.
потенциальным
и найти его потенциал.
Решение.
Если плоское поле вектора
![]() потенциально, то
потенциально, то 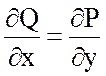 .
.
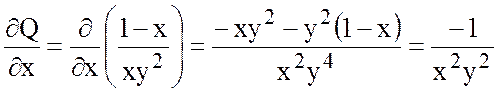 ,
,
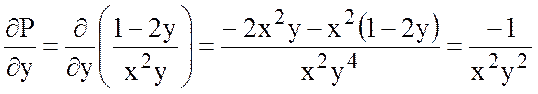 .
.
Так как 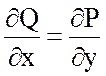 , то поле потенциально. Найдем
потенциал.
, то поле потенциально. Найдем
потенциал.
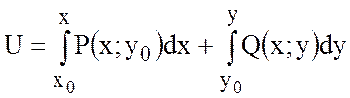 .
.
В качестве точки ![]() возьмем точку (1;1). Точку (0;0)
брать нельзя, так как в этой точке поле вектора
возьмем точку (1;1). Точку (0;0)
брать нельзя, так как в этой точке поле вектора ![]() не
задано, функции Р и Q не существуют в
(0;0).
не
задано, функции Р и Q не существуют в
(0;0).
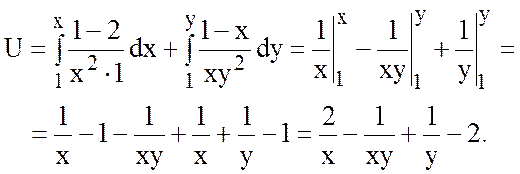
Проверка: 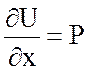 ,
, 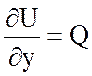 .
.
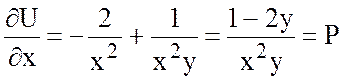 ,
,
 .
.
Ответ:  .
.
13 Циркуляция векторного поля
Определение:Циркуляцией вектора ![]() вдоль
замкнутого контура L называется
криволинейный интеграл по этому контуру от скалярного произведения вектора
вдоль
замкнутого контура L называется
криволинейный интеграл по этому контуру от скалярного произведения вектора ![]() на вектор
на вектор ![]() касательной
к контуру:
касательной
к контуру:
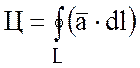 ,
,
если ![]() и
и ![]() ,
то
,
то
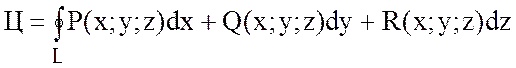 (6)
(6)
Положительным направлением обхода замкнутой кривой L считают направление, при котором область, ограниченная этой кривой, будет оставаться слева.
В силовом поле формула (6) выражает работу при перемещении материальной точки вдоль линии L.
Пример.
1) Найти циркуляцию
векторного поля ![]() вдоль линии эллипса
вдоль линии эллипса 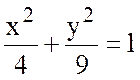
Решение.
По определению циркуляции имеем:
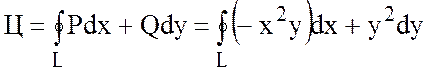 .
.
Так как 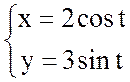 - параметрическое уравнение эллипса,
то
- параметрическое уравнение эллипса,
то
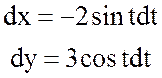 , при этом
, при этом ![]() .
.
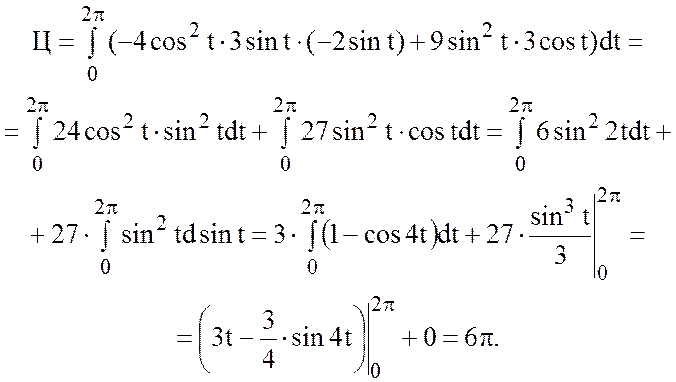
2) Найти циркуляцию векторного поля
![]() вдоль
линии пересечения плоскости
вдоль
линии пересечения плоскости ![]() с координатными
плоскостями.
с координатными
плоскостями.
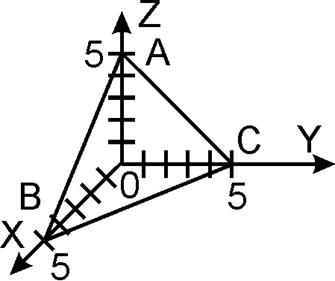
|
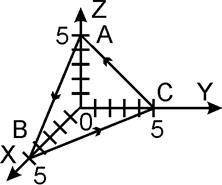
Линиями пересечения плоскости
![]() с координатными плоскостями будут
стороны треугольника АВС, т.е.
с координатными плоскостями будут
стороны треугольника АВС, т.е.
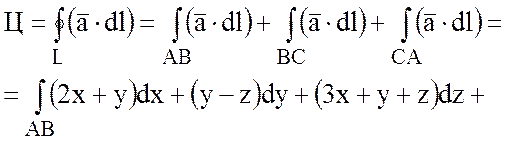
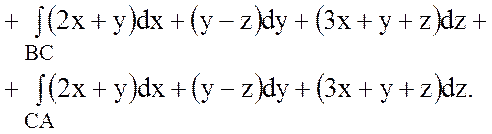
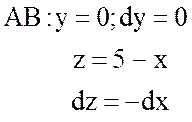 ;
; 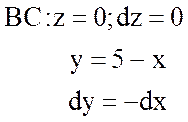 ;
;
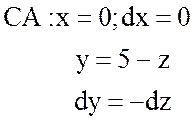 .
.
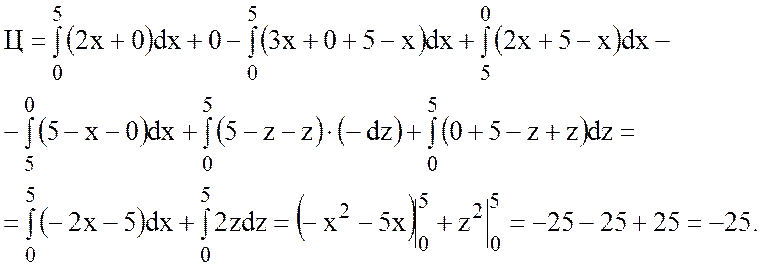
14 Формула Стокса
Пусть координаты вектора ![]() непрерывны и имеют непрерывные
частные производные, тогда циркуляцию вектора
непрерывны и имеют непрерывные
частные производные, тогда циркуляцию вектора ![]() по
замкнутому контуру L удобно вычислить
по формуле Стокса.
по
замкнутому контуру L удобно вычислить
по формуле Стокса.
Теорема:Циркуляция вектора ![]() по
замкнутому контуру L равна потоку
ротора этого вектора через любую поверхность S, натянутую на контур L.
по
замкнутому контуру L равна потоку
ротора этого вектора через любую поверхность S, натянутую на контур L.
 .
.
Предполагается, что
ориентация нормали ![]() к поверхности S согласована с ориентацией контура L так, чтобы из конца нормали обход
контура в выбранном направлении был виден совершающимся против часовой стрелки.
к поверхности S согласована с ориентацией контура L так, чтобы из конца нормали обход
контура в выбранном направлении был виден совершающимся против часовой стрелки.
Так как

 , а
, а ![]() ,
то
,
то
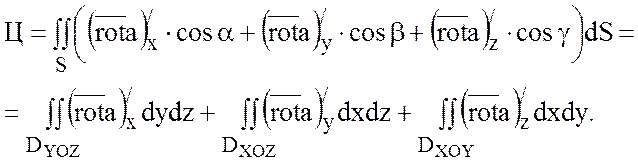
Так как
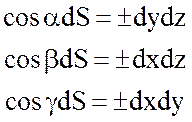 .
.
Из теоремы следует формула Стокса:
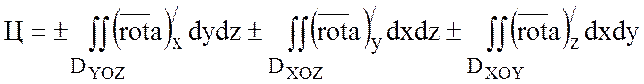 ,
,
где ![]() - проекции поверхности S на плоскости YOZ, XOZ, XOY.
- проекции поверхности S на плоскости YOZ, XOZ, XOY.
Из формулы Стокса
следует, что если поле вектора ![]() потенциально, то
тогда
потенциально, то
тогда ![]() =0 и циркуляция вектора
=0 и циркуляция вектора ![]() потенциального поля равна нулю
потенциального поля равна нулю
Частным случаем формулы
Стокса, когда поле вектора ![]() плоское, будет
формула Грина.
плоское, будет
формула Грина.
Если поле вектора ![]() плоское, то
плоское, то
![]() ,
,
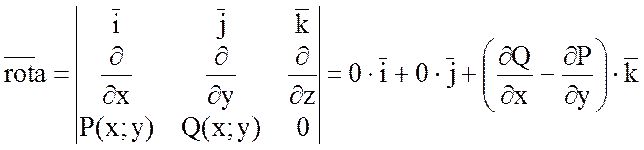 ,
,
так как 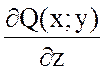 =0 и
=0 и 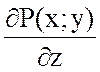 =0.
=0.
Тогда в формуле Стокса  =0 и
=0 и 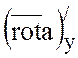 =0
и
=0
и
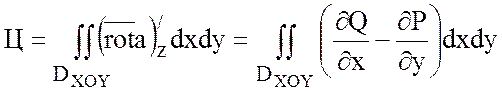 .
.
Примеры.
1) Решим второй пример из рассмотренных ранее вторым способом по формуле Стокса.
Найти циркуляцию векторного поля
![]() вдоль
линии пересечения плоскости
вдоль
линии пересечения плоскости ![]() с координатными
плоскостями.
с координатными
плоскостями.
Решение.
Найдем ![]() :
:
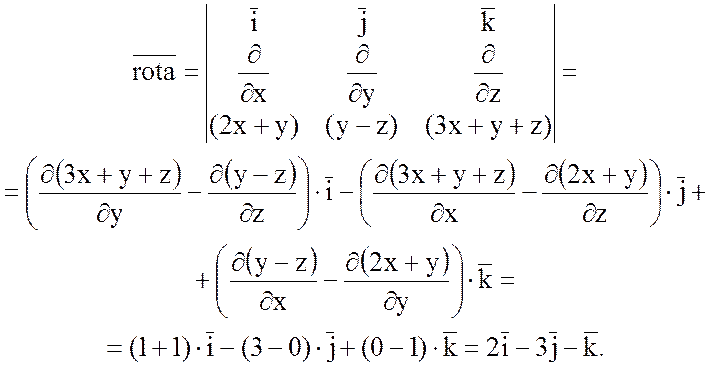
Тогда  =2,
=2,  =-3,
=-3,
 =-1.
=-1.
Найдем циркуляцию по формуле Стокса:
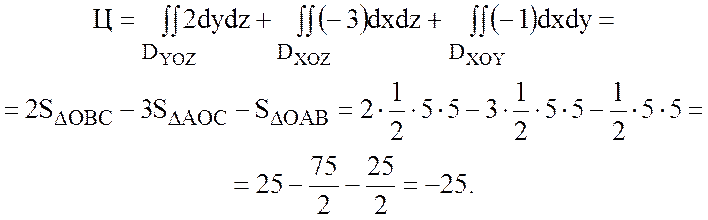
2) Вычислить циркуляцию
вектора ![]() по контуру L, образованному линиями y=x,
по контуру L, образованному линиями y=x, ![]() .
.
Решение.
Так как поле вектора ![]() плоское, то найдем циркуляцию по
формуле Грина:
плоское, то найдем циркуляцию по
формуле Грина:
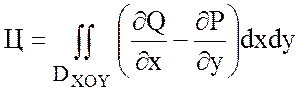 .
.
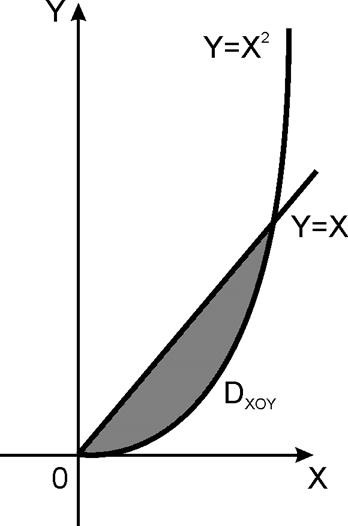
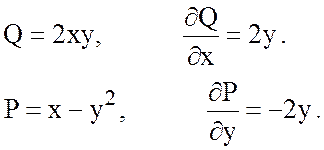
Рисунок 17
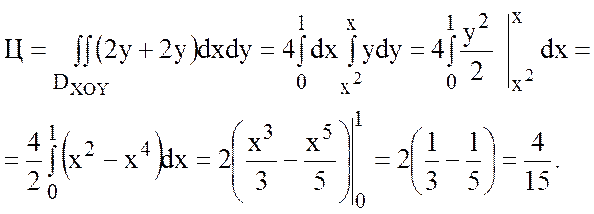
15 Оператор Гамильтона. Векторные дифференциальные операции второго порядка
Многие операции векторного анализа могут быть записаны в сокращенной и удобной для расчетов форме с помощью символического оператора Гамильтона «набла».
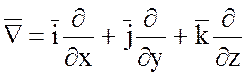 .
.
В этом операторе
соединены дифференциальные и векторные свойства. Формальное умножение ![]() на функцию U(x;y;z) понимают как частное дифференцирование
на функцию U(x;y;z) понимают как частное дифференцирование ![]() .
.
Правила действия с оператором «набла» таковы:
1) Произведение набла –
вектора ![]() на скалярную функцию U(x;y;z) дает градиент этой функции:
на скалярную функцию U(x;y;z) дает градиент этой функции:
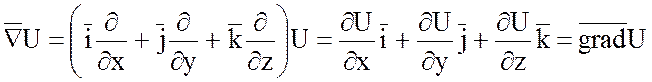 .
.
2) Скалярное произведение
набла - вектора ![]() на векторную функцию
на векторную функцию ![]() дает дивергенцию этой функции:
дает дивергенцию этой функции:
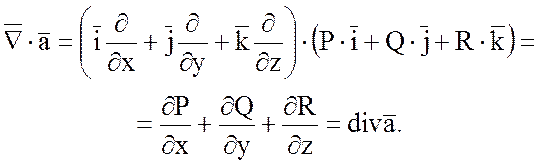
3) Векторное произведение
набла – вектора ![]() на векторную функцию
на векторную функцию ![]() дает ротор этой функции:
дает ротор этой функции:
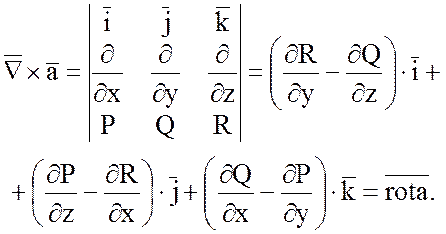
Рассмотрим теперь векторные дифференциальные операции второго порядка.
Пусть задано скалярное
поле U(x;y;z) и нашли градиент этого поля ![]() . Поле градиента является векторным
полем и можно найти его дивергенцию и ротор, т.е.
. Поле градиента является векторным
полем и можно найти его дивергенцию и ротор, т.е. ![]() и
и
![]() .
.
а)  . (*)
. (*)
Действительно, 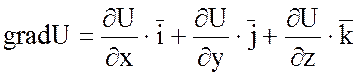 , образуя дивергенцию этого вектора,
мы и получим данную формулу (*). Правая часть формулы (*) называется оператором
Лапласа от функции и обозначается
, образуя дивергенцию этого вектора,
мы и получим данную формулу (*). Правая часть формулы (*) называется оператором
Лапласа от функции и обозначается ![]() :
:
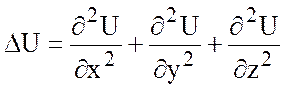 .
.
Выражение ![]() можно с помощью набла – вектора
записать так:
можно с помощью набла – вектора
записать так:
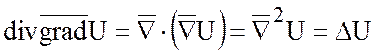 .
.
б) Пусть функция U(x;y;z) имеет непрерывные частные
производные до второго порядка включительно, тогда ![]() =0.
=0.
Это равенство проверяется
просто, так как все координаты ![]() представляют
собой разность вторых смешанных производных функции U, отличающихся лишь порядком дифференцирования, которые
равны, например:
представляют
собой разность вторых смешанных производных функции U, отличающихся лишь порядком дифференцирования, которые
равны, например:
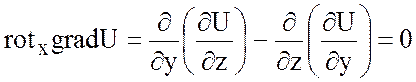 .
.
Это соотношение легко запоминается, если записать его с помощью набла – вектора:
![]() ,
,
так как векторное произведение одинаковых «векторов» равно нулю.
в) ![]() .
.
Образуя дивергенцию от ![]() , получим:
, получим:
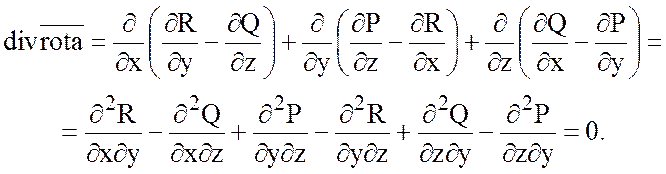
Так как вторые смешанные производные равны, если функции P, Q, R имеют непрерывные частные производные до второго порядка включительно.
С помощью набла – вектора это запишется так:
![]() .
.
То есть мы имеем смешанное произведение трех «векторов», из которых два вектора одинаковы. Такое произведение равно нулю.
16 Семестровое задание по теме «Теория поля»
Решение задач.
Задача 1.
а) Найти угол между
градиентами функции ![]() в точках (1;-1;0) и
(2;1;1).
в точках (1;-1;0) и
(2;1;1).
Решение.
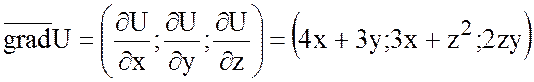 .
.
Найдем градиент функции U в точках (1;-1;0) и (2;1;1):
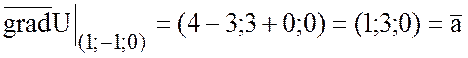 ,
,
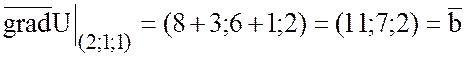 .
.
Тогда косинус угла ![]() между градиентами, т.е. между
векторами
между градиентами, т.е. между
векторами ![]() и
и ![]() найдем
по формуле:
найдем
по формуле:
 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.