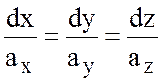 , т.е
, т.е 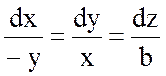 .
.
Решая 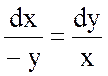 , получим
, получим ![]() ,
,
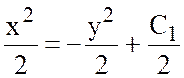 , или
, или ![]() .
Если ввести параметр t, то
получим параметрические уравнения окружности:
.
Если ввести параметр t, то
получим параметрические уравнения окружности:
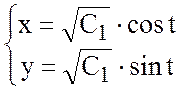 .
.
Тогда уравнение 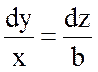 примет вид:
примет вид:
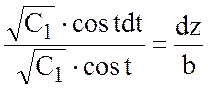 или
или ![]() ,
,
тогда
![]() .
.
Следовательно, параметрические уравнения векторных линий будут такими:
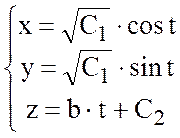 .
.
Если векторная линия проходит через точки (1;0;0), то
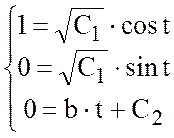 .
.
Тогда ![]() =1,
=1, ![]() =0
и через точку (1;0;0) проходит векторная линия с уравнением:
=0
и через точку (1;0;0) проходит векторная линия с уравнением:
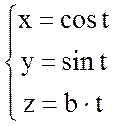 .
.
Это уравнение винтовой линии.
2) Найти векторные линии
плоского поля ![]() .
.
Решение.
Уравнение векторных линий такое:
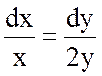 .
.
Проинтегрировав, получим
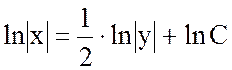 ,
, ![]() .
.
Это семейство ветвей параболы:
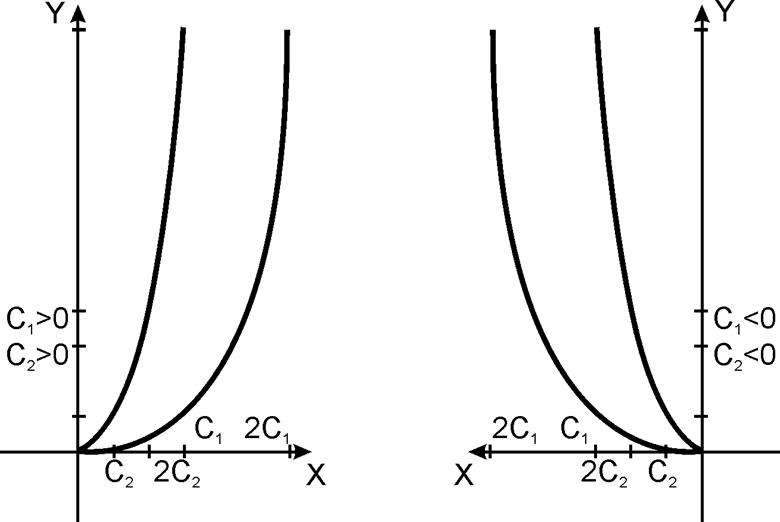
Рисунок 5 Рисунок 6
6 Поток векторного поля
Пусть векторное поле образовано вектором
![]() .
.
Возьмем в этом поле
некоторую поверхность S,
которая предполагается двусторонней, и выберем на ней определенную сторону.
Пусть ![]() - единичный вектор нормали к
рассматриваемой стороне поверхности в произвольной точке поверхности.
- единичный вектор нормали к
рассматриваемой стороне поверхности в произвольной точке поверхности.
Потоком вектора ![]() через поверхность S называется поверхностный интеграл
1-го рода по поверхности S от
скалярного произведения вектора
через поверхность S называется поверхностный интеграл
1-го рода по поверхности S от
скалярного произведения вектора ![]() на единичный
вектор нормали к поверхности
на единичный
вектор нормали к поверхности ![]() .
.
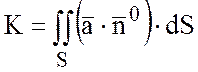 .
.
Вычислить поток вектора – это вычислить поверхностный интеграл 1-го рода.
Свойства потока
1) Поток вектора величина скалярная.
2) Поток меняет знак на
обратный с изменением ориентации поверхности (т.е. с изменением ориентации
нормали ![]() к поверхности S):
к поверхности S):
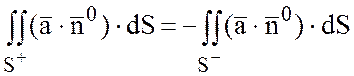 ,
,
где ![]() - сторона поверхности S, на которой выбрана нормаль
- сторона поверхности S, на которой выбрана нормаль ![]() ,
, ![]() -
сторона поверхности S, на которой
нормаль
-
сторона поверхности S, на которой
нормаль ![]() .
.
3) Свойство линейности:
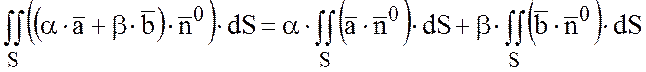 ,
,
где ![]() и
и ![]() -
числа.
-
числа.
4) Свойство аддитивности:
если поверхность S состоит из
нескольких гладких частей ![]() ,
, ![]() , ...
, ... ![]() ,
то поток векторного поля вектора
,
то поток векторного поля вектора ![]() через S равен сумме потоков вектора
через S равен сумме потоков вектора ![]() через поверхности
через поверхности ![]() ,
, ![]() ,
...
,
... ![]() :
:
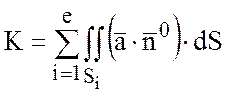 .
.
Пусть поверхность S замкнутая и ограничивает некоторую
область ![]() . Возьмем внешнюю нормаль и
рассмотрим поток изнутри поверхности S.
. Возьмем внешнюю нормаль и
рассмотрим поток изнутри поверхности S.
Когда векторное поле ![]() представляет поле скоростей
жидкости, величина потока К дает разность между количеством жидкости,
вытекающей из области
представляет поле скоростей
жидкости, величина потока К дает разность между количеством жидкости,
вытекающей из области ![]() , и количеством жидкости,
втекающей в эту область. Если К=0, то в область
, и количеством жидкости,
втекающей в эту область. Если К=0, то в область ![]() втекает
столько же жидкости, сколько и вытекает. Так будет для любой области,
расположенной в потоке воды, текущей в реке.
втекает
столько же жидкости, сколько и вытекает. Так будет для любой области,
расположенной в потоке воды, текущей в реке.
Если К>0, то вытекает
жидкости больше, чем втекает, т.е. в области ![]() имеются
источники, питающие поток жидкости.
имеются
источники, питающие поток жидкости.
Если К<0, то вытекает жидкости меньше, чем втекает, тогда в области есть стоки, где жидкость удаляется из потока.
7 Способы вычисления потока
7.1 Метод проектирования на все три координатные плоскости
Пусть поверхность S взаимно – однозначно проектируется
на все три координатные плоскости. Пусть ![]() ,
, ![]() ,
, ![]() проекции
поверхности S соответственно на плоскости XOY, XOZ и YOZ.
проекции
поверхности S соответственно на плоскости XOY, XOZ и YOZ.
Пусть уравнение
поверхности S: ![]() = 0 однозначно разрешимо
относительно каждого из аргументов x, y, z.
= 0 однозначно разрешимо
относительно каждого из аргументов x, y, z.
x=x(y,z), y=y(x,z), z=z(x,y).
Тогда поток вектора ![]() через поверхность S с единичным вектором нормали
через поверхность S с единичным вектором нормали ![]() , где
, где ![]() ,
, ![]() ,
, ![]() -
направляющие косинусы нормали, будет вычисляться так:
-
направляющие косинусы нормали, будет вычисляться так:
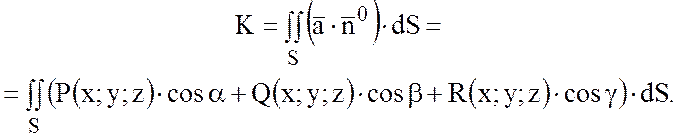
т.к. 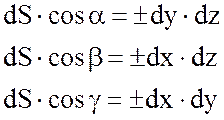 , то
, то
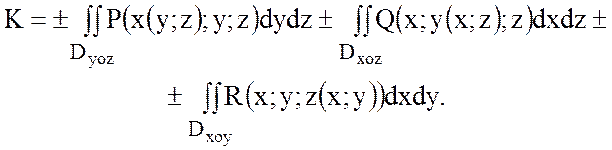
Знак «+» или «-»
выбирается так, чтобы он совпадал у первого слагаемого со знаком ![]() , у второго слагаемого со знаком
, у второго слагаемого со знаком ![]() , у третьего со знаком
, у третьего со знаком ![]() на поверхности S.
на поверхности S.
При этом орт ![]() нормали к выбранной стороне
поверхности находится по формуле:
нормали к выбранной стороне
поверхности находится по формуле:
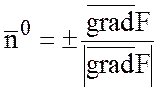 ,
,
где F(x;y;z)=0 – уравнение поверхности S.
Знак выбирается согласно с выбором нормали к поверхности S.
Пример.
Найти поток вектора ![]() через треугольник, вырезанный из
плоскости Р координатными плоскостями, в том направлении нормали к плоскости,
которое образует с осью ОХ острый угол. Уравнение плоскости Р: x-y+2z+5=0.
через треугольник, вырезанный из
плоскости Р координатными плоскостями, в том направлении нормали к плоскости,
которое образует с осью ОХ острый угол. Уравнение плоскости Р: x-y+2z+5=0.
Решение.
Найдем орт ![]() нормали к поверхности:
нормали к поверхности:
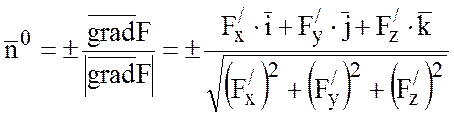 .
.
так как F(x;y;z)=x-y+2z+5=0, то
![]() =1,
=1, ![]() =-1,
=-1, ![]() =2.
=2.
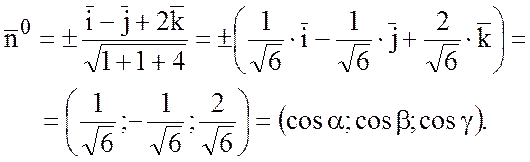
Выбрали знак «+», так как
по условию задачи сказано, что угол ![]() острый, т.е.
острый, т.е. ![]() >0.
>0.
Найдем теперь поток по формуле:
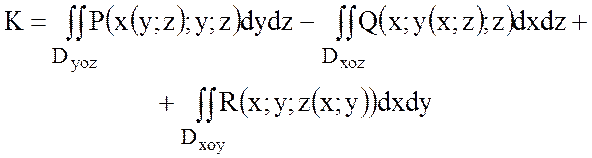 ,
,
где второй член с «-»,
так как ![]() <0.
<0.
Т.е.
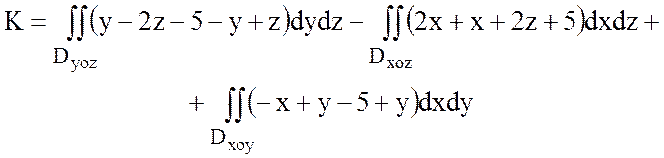 ,
,
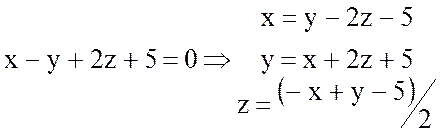 .
.
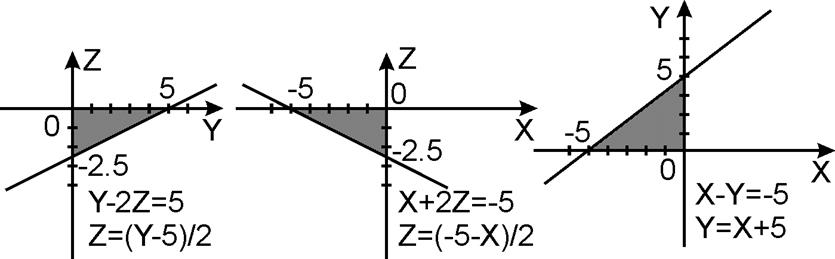
Рисунок 7 Рисунок 8 Рисунок 9
На рисунках 7,8,9 показаны проекции поверхности S на ZOY (рис.1), XOZ (рис.2) и XOY (рис.3).
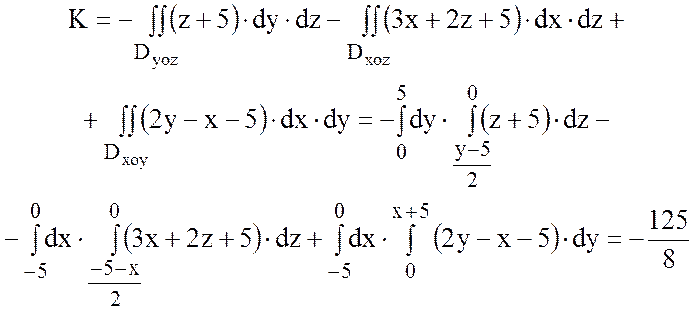
7.2 Вычисление потока проектированием на одну из координатных плоскостей
Вычислим поток проектированием на плоскость XOY.
Если незамкнутая
поверхность S имеет уравнение F(x;y;z)=0 и взаимно однозначно
проектируется на плоскость XOY в
область ![]() . Уравнение F(x;y;z)=0 однозначно разрешимо относительно z, т.е.
. Уравнение F(x;y;z)=0 однозначно разрешимо относительно z, т.е. ![]() .
.
Так как элемент площади dS этой поверхности равен
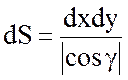 , то
, то 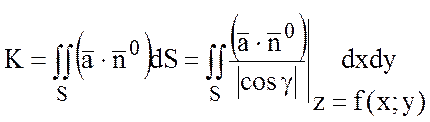 .
.
Орт нормали ![]() к выбранной стороне поверхности
находим по формуле:
к выбранной стороне поверхности
находим по формуле:
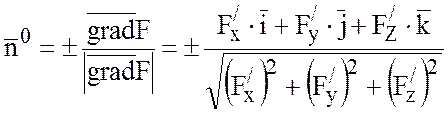 ,
,
тогда ![]() равен коэффициенту при
равен коэффициенту при ![]() , т.е.
, т.е.
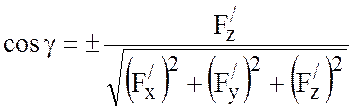 (3)
(3)
Если угол ![]() между осью oz и нормалью
между осью oz и нормалью ![]() острый, то в
формуле (3) берем знак «+», если же угол тупой, то берется «-».
острый, то в
формуле (3) берем знак «+», если же угол тупой, то берется «-».
Решим ранее рассматриваемую задачу проектированием на плоскость XOY.
Задача.
Найти поток вектора ![]() через треугольник, вырезанный из
плоскости Р координатными плоскостями, в том направлении нормали к плоскости,
которое образует с осью ОХ острый угол. Уравнение плоскости Р: x-y+2z+5=0.
через треугольник, вырезанный из
плоскости Р координатными плоскостями, в том направлении нормали к плоскости,
которое образует с осью ОХ острый угол. Уравнение плоскости Р: x-y+2z+5=0.
Решение.
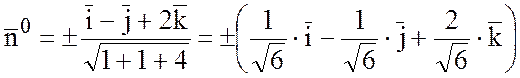 (4)
(4)
Так как по условию задачи
сказано, что орт нормали к плоскости Р образует острый угол с осью ox, т.е. ![]() ,
то в формуле (4) выберем знак «+». Тогда
,
то в формуле (4) выберем знак «+». Тогда 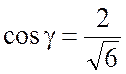 .
.
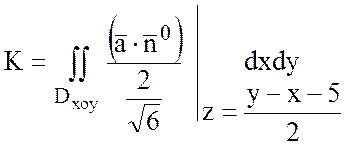
Найдем ![]() :
:
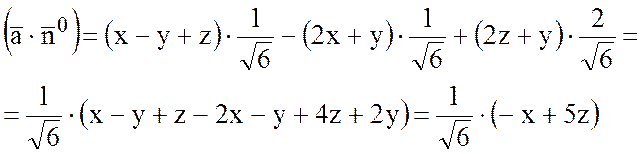 ,
,
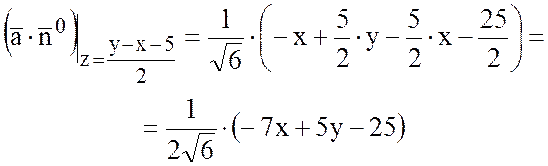
Тогда
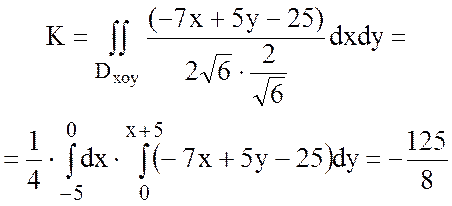
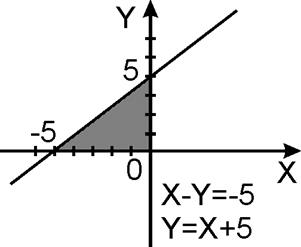
Если оказывается удобным проектировать поверхность S на координатные плоскости YOZ или XOZ, то для вычисления потока пользуются соответственно формулами:
Рисунок 10
 (5)
(5)
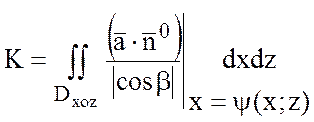 (6)
(6)
Рассмотрим решение еще одной задачи о нахождении потока через незамкнутую поверхность S проектированием на одну из координатных плоскостей.
Задача.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.