Теория поля: Методические указания к выполнению семестрового задания (с вариантами заданий), страница 3

Найти поток векторного поля  через треугольник, вырезанный из плоскости Р координатными плоскостями, в том направлении нормали к плоскости, которое образует с осью oz тупой угол. Уравнение плоскости Р: 2x-y+5z-10=0

Решение.

Найдем орт нормали  к плоскости Р:

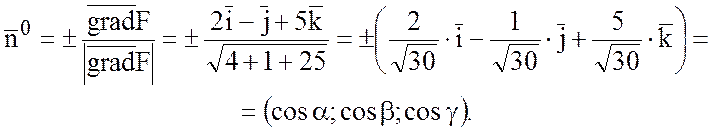
Так как по условию задачи угол между  и осью oz тупой, то <0, поэтому выбираем знак «-»

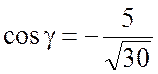, тогда .

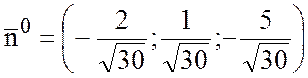Найдем :

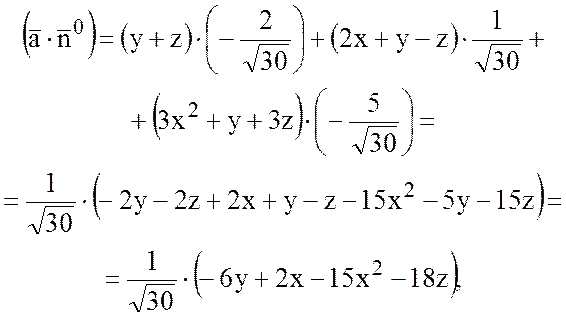
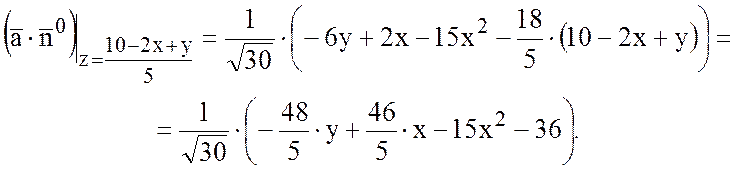
Тогда, так как 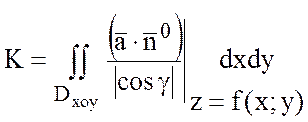, то

Рисунок 11

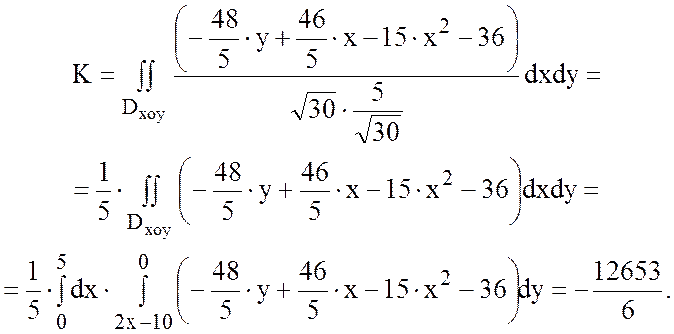
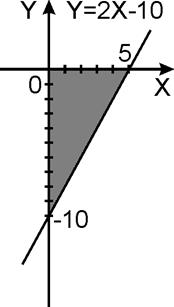
8 Формула Остроградского – Гаусса

Если в некоторой области D пространства координаты вектора  непрерывны и имеют непрерывные частные производные , , , то поток вектора  через любую замкнутую поверхность S, расположенную в области D, равен тройному интегралу от 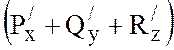 по области V, ограниченной поверхностью S, т.е.:

.

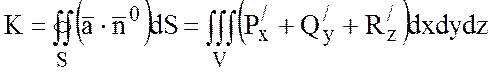Вычисление потока по формуле Остроградского – Гаусса значительно облегчает нахождение потока, когда поверхность S замкнутая.

Задача.

Решить задачу о нахождении потока вектора  через замкнутую поверхность S по формуле Остроградского – Гаусса, если  и S: , z=4.

Решение.

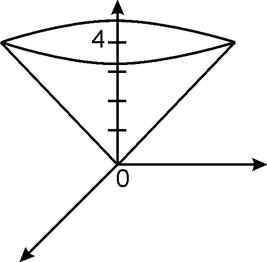
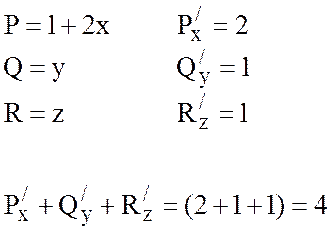
Рисунок 12

Тогда

.

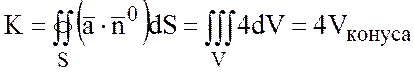Так как объем конуса

.

Тогда

.

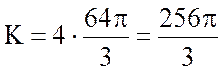Ответ: .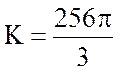

Рассмотрим решение еще одной задачи.

Задача.

Найти поток вектора  через поверхность пирамиды, образованной плоскостью 3x+y+5z-15=0 и координатными плоскостями, если .

Решение.

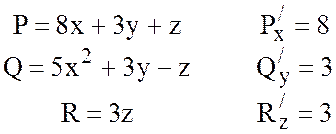
Тогда

,

.

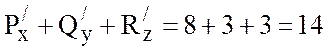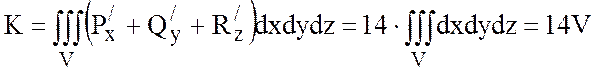V – объем пирамиды, образованной плоскостью 3x+y+5z-15=0 и координатными плоскостями.

Рисунок 13

.

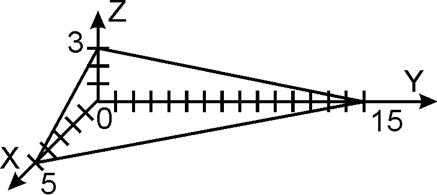
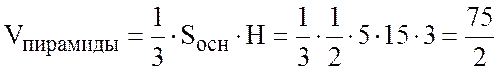Тогда

.

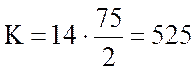Ответ: К=525.

9 Дивергенция векторного поля

Возьмем некоторую точку Р векторного поля , окружим ее замкнутой поверхностью S, которая полностью находится в поле. Вычислим поток вектора  через поверхность S и рассмотрим отношение этого потока к объему V области , ограниченной поверхностью S.

.

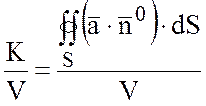В поле скоростей жидкости это отношение характеризует среднюю объемную мощность источника, если К>0 или среднюю объемную мощность стока, если К<0.

Найдем теперь предел отношения

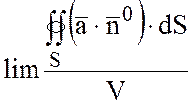 при условии, что область  стягивается в точку Р, т.е что объем .

Определение.

Дивергенцией векторного поля  в точке Р называется предел отношения потока вектора через поверхность, окружающую точку Р, к объему, ограниченному этой поверхностью, при условии, что вся поверхность стягивается в точку Р.

.

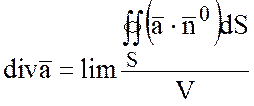Теорема.

Дивергенцией векторного поля  в точке Р выражается формулой 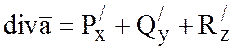, где частные производные берутся в точке Р.

Доказательство.

По формуле Остроградского-Гаусса 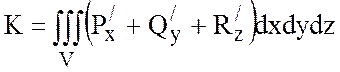 и по теореме о среднем тройной интеграл равен произведению объема V на значение подынтегральной функции в некоторой точке  области , т.е.

.

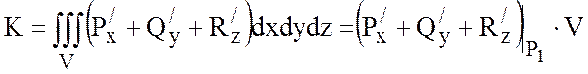Если область  стягивается в точку Р, то точка  стремится к точке Р и тогда

.

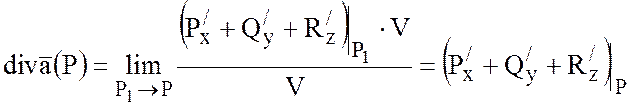Из определения дивергенции следует, что если , то в точке Р – источник, а если , то в точке Р – сток.

Определение.

Если во всех точках некоторой области Д дивергенция векторного поля  (заданного в области Д) равна нулю , то говорят, что поле соленоидально в этой области.

Примеры.

1) Найти дивергенцию векторного поля

.

Решение.

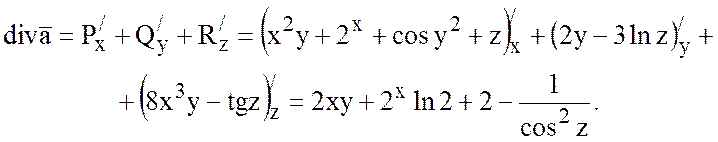
2) Будет ли в точке Р(1;-1;1) векторного поля

 источник или сток.

Решение.

.

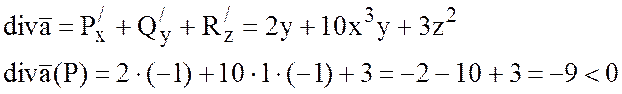Так как , то в точке Р сток.

3) Проверить, будет ли поле вектора

 соленоидальным.

Решение.

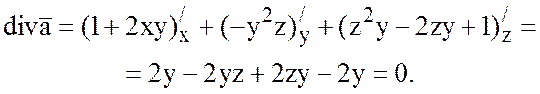
Так как , то поле соленоидально.

10 Ротор векторного поля

Определение:Ротором векторного поля

 называется вектор

.

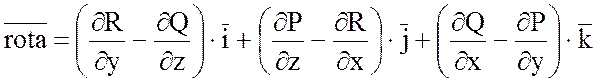Для удобства запоминания  удобно находить в символической форме:

.

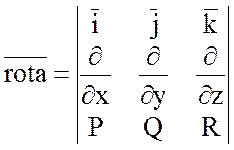Этот определитель раскрывается по элементам первой строки, при этом операции умножения элементов второй строки на элементы третьей строки понимаются как операции дифференцирования, например .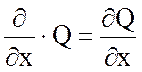

Определение:Если в некоторой области Д =0, то поле вектора  в области Д называется безвихревым.

Примеры.

1) Найти ротор векторного поля .

Решение.

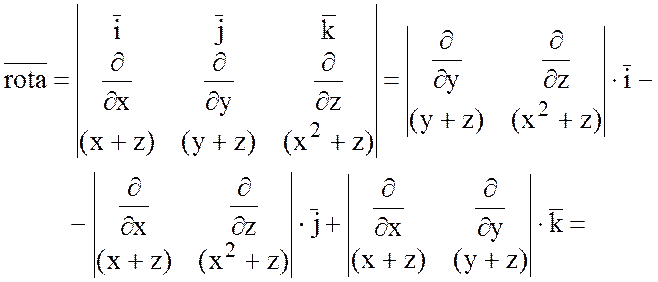
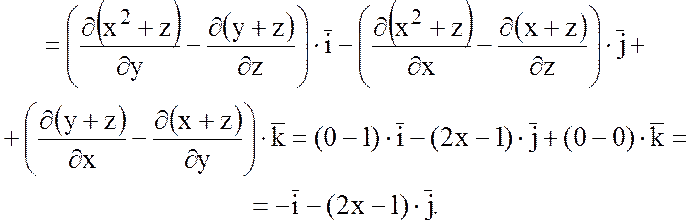
2) Какова должна быть функция f(x;z), чтобы ротор векторного поля  совпадал с вектором ?

Решение.

,

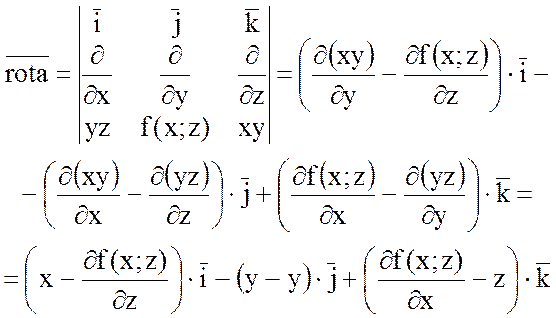
тогд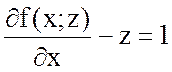а

, а .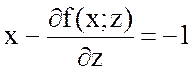

Получили систему:

.

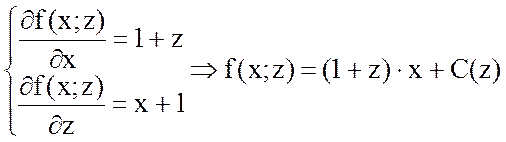Подставив во второе уравнение системы, получим:

.

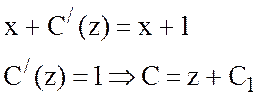Тогда , где  - константа.

Ответ: .

11 Потенциальное поле

Определение:Векторное поле

  называется потенциальным, если существует такая функция , что во всех точках, где поле задано, выполняется равенство:

 или , , .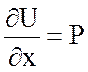

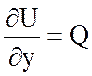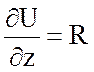При этом функция U называется потенциалом векторного поля или его потенциальной функцией.

12 Критерий потенциальности векторного поля

Для того, чтобы векторное поле, заданное в односвязной области V вектором , было потенциальным, необходимо и достаточно, чтобы в каждой точке области, где задано поле, выполнялось условие .

Определение:Область V односвязная, если на любой замкнутый контур, лежащий в этой области, можно натянуть поверхность, целиком лежащую в области V.

Иначе говоря, поле потенциально, если оно безвихревое, т.е. выполняется равенство:

.

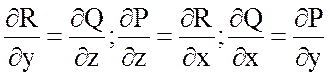Если векторное поле плоское, т.е. , то оно потенциально, если 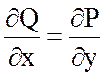, так как в этом случае .

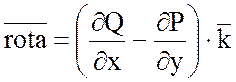Если поле потенциально, то криволинейные интегралы, вычисляемые вдоль кривых, находящихся в области, где задано это поле, не зависят от пути интегрирования, а зависят только от начала и конца движения по кривой. Это происходит, т.к. условие потенциальности поля совпадает с условием независимости криволинейного интеграла от пути интегрирования.

Потенциал находим по формуле:

.

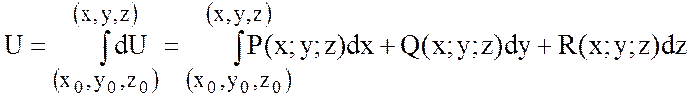И так как нет зависимости от пути интегрирования, то из точки  в точку  будем двигаться параллельно осям координат:

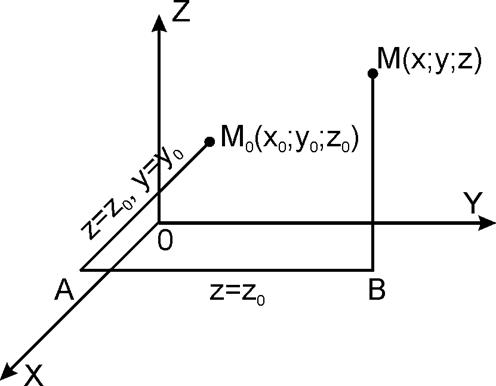
Рисунок 14

Тогда

.

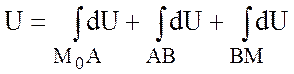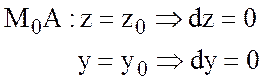; Тогда .

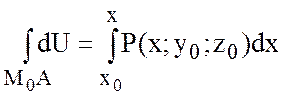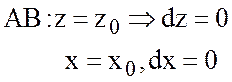; Тогда .

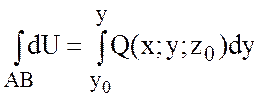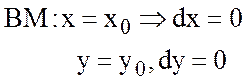; Тогда .

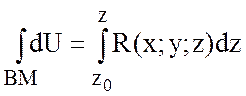Тогда полный дифференциал можно найти по формуле:

.

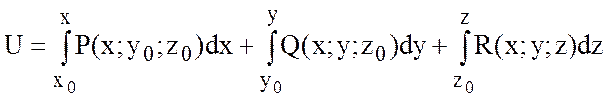Если поле плоское, то

.

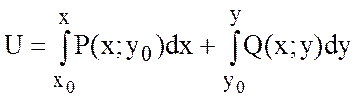Потенциал поля определяется неоднозначно, с точностью до постоянного слагаемого, так как точка  выбирается произвольно. Чаще в качестве точки  берут (0;0;0), если это точка, в которой поле вектора  задано.