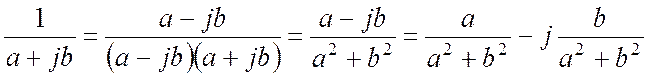 . (18.11)
. (18.11)
Из свойств комплексных токов и напряжений следует вывод, что любой комплексный ток и любое комплексное напряжение можно разложить на две составляющие – действительную и мнимую. Действительная составляющая соответствует активной мощности, мнимая составляющая соответствует реактивной мощности.
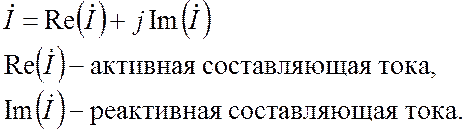 (18.12)
(18.12)
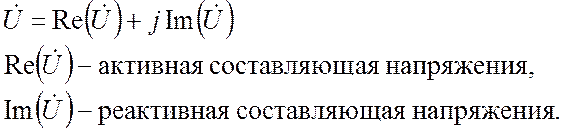 (18.13)
(18.13)
Если комплексное напряжение на участке цепи поделить на комплексный ток этого участка, получим параметр, называемый комплексным сопротивлением. Комплексное сопротивление также имеет активную и реактивную составляющие:
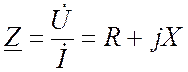 , (18.14)
, (18.14)
где R – активное сопротивление;
X – реактивное сопротивление.
Следует
заметить, что реактивное сопротивление может быть индуктивным или емкостным. В
комплексной форме индуктивное сопротивление всегда умножается на ![]() (это связано с тем, что на
индуктивности напряжение опережает ток на
(это связано с тем, что на
индуктивности напряжение опережает ток на ![]() ),
а емкостное сопротивление всегда умножается на
),
а емкостное сопротивление всегда умножается на ![]() (это
связано с тем, что на емкости напряжение отстает от тока на
(это
связано с тем, что на емкости напряжение отстает от тока на ![]() ).
).
Модуль комплексного сопротивления:
![]()
называется полным сопротивлением участка цепи (его устаревшее, но иногда встречающееся название – импеданс).
Величина, обратная комплексному сопротивлению, называется комплексной проводимостью:
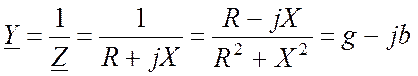 , (18.15)
, (18.15)
где g – активная проводимость;
b – реактивная проводимость.
Активная, реактивная составляющие и модуль тока, собранные воедино, образуют прямоугольный треугольник, называемый треугольником токов (Рис. 18.8 а). Аналогично получают треугольник напряжений (Рис. 18.8 б). Треугольник напряжений, деленный на треугольник токов, дает треугольник сопротивлений (Рис. 18.8 в).
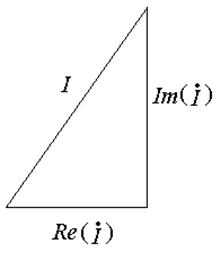
а)
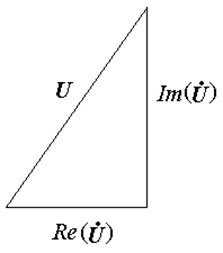
б)
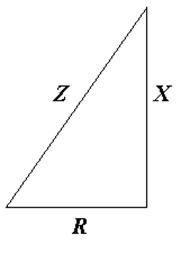
в)
Рис. 18.8
Комплексное напряжение и комплексный ток связаны между собой законом Ома в комплексной форме, который формулируется аналогично закону Ома для цепей постоянного тока:
![]() , (18.16)
, (18.16)
Комплексное напряжение на участке цепи, не содержащем ЭДС, равно произведению комплексного тока на этом участке на комплексное сопротивление.
Законы Кирхгофа в комплексной форме формулируются аналогично законам Кирхгофа в теории цепей постоянного тока.
Первый закон Кирхгофа: В любом узле цепи сумма комплексных токов равна нулю.
Второй закон Кирхгофа: В любом замкнутом контуре цепи сумма комплексных напряжений равна сумме комплексных ЭДС, включенных в контур.
Законы Ома и Кирхгофа в комплексной форме можно применять для расчетов цепей синусоидального тока.
Пример 18.1
Составить систему уравнений Кирхгофа в комплексной форме и определить токи (Рис. 18.9):
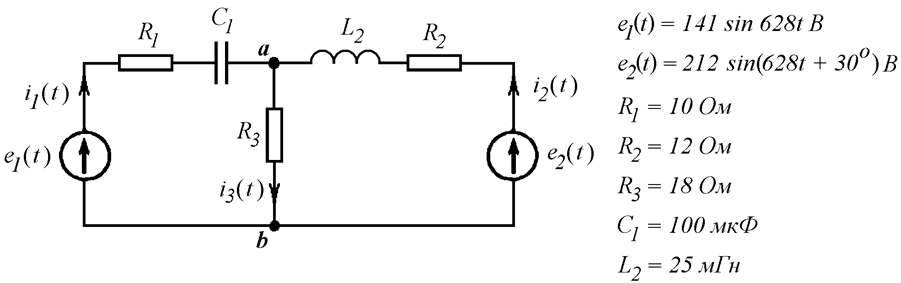
Рис. 18.9
Стрелки на схеме показывают условное направление токов и ЭДС, которого надо придерживаться в процессе расчетов.
Рассчитываем комплексные ЭДС цепи (для действующих значений). Делить комплексные числа удобно в показательной форме. При этом модули делятся, углы вычитаются:
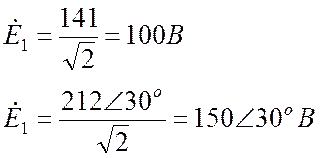 .
.
Для удобства
комплексные числа записывают в форме «![]() »
и читают: «Сто пятьдесят под углом тридцать градусов вольт».
»
и читают: «Сто пятьдесят под углом тридцать градусов вольт».
Рассчитываем реактивные сопротивления:
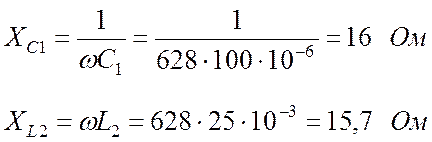 .
.
Составляем схему для расчетов в символической форме. Синусоидальные ЭДС заменяем комплексными. Реактивные элементы заменяем их сопротивлениями (Рис. 18.10).
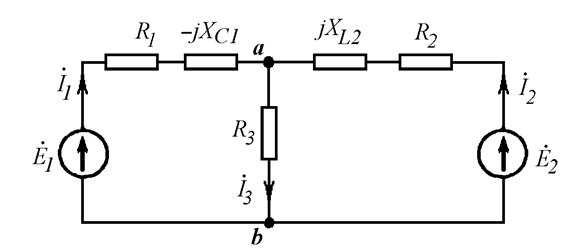
Рис. 18.10
Обратить
внимание: сопротивление ![]() – емкостное,
поэтому оно умножается на
– емкостное,
поэтому оно умножается на ![]() (удобно отмечать
это прямо на схеме), сопротивление
(удобно отмечать
это прямо на схеме), сопротивление ![]() – индуктивное,
поэтому оно умножается на
– индуктивное,
поэтому оно умножается на ![]() .
.
Выбираем направление обхода контуров (Рис. 18.11) и составляем систему уравнений Кирхгофа:
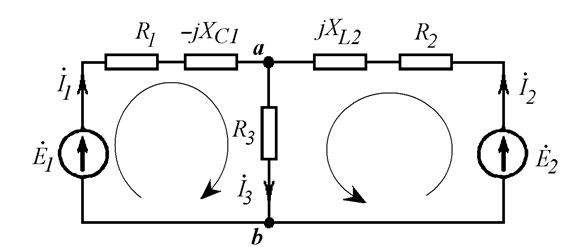
Рис. 18.11
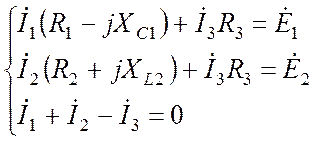 .
.
Подставляем в систему числовые параметры:
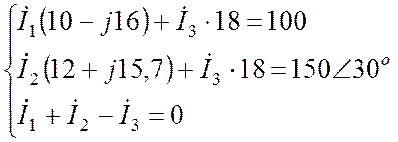 .
.
Получившуюся
систему уравнений можно решать любым удобным методом. Например, можно упростить
ее, исключив третье уравнение и ток ![]() :
:
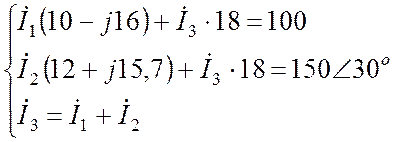 .
.
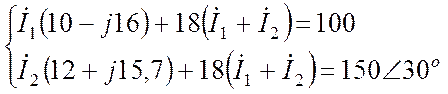 .
.
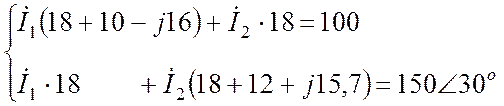 .
.
Решаем систему уравнений методом Крамера:
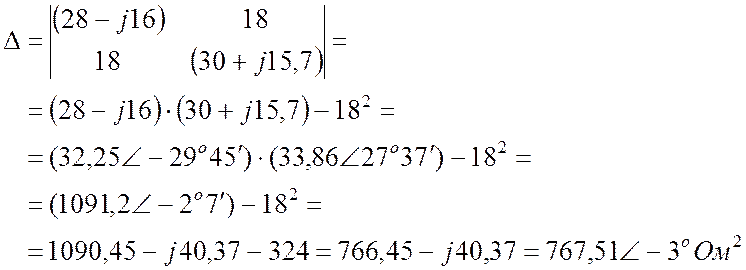 .
.
Комплексные числа удобно умножать в показательной форме (модули перемножаются, углы складываются), а складывать и вычитать – в алгебраической форме (действительные части складываются с действительными, мнимые части – с мнимыми).
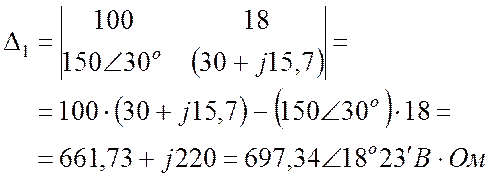 .
.
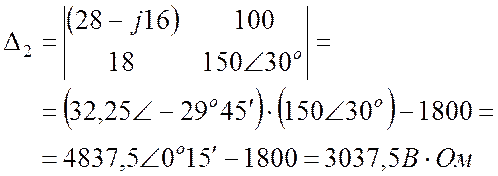 .
.
Комплексные токи:
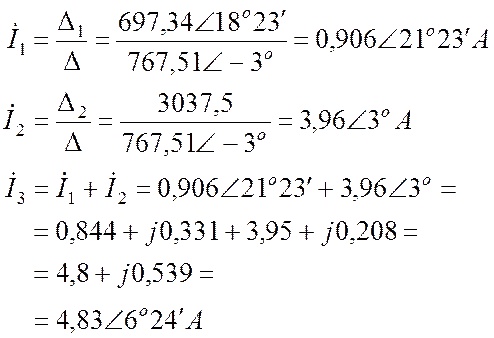 .
.
Записываем мгновенные значения токов:
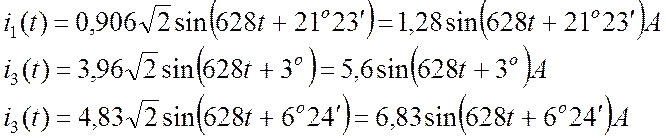 .
.
19. МОЩНОСТЬ СИНУСОИДАЛЬНОГО РЕЖИМА
Рассмотрим некоторый пассивный двухполюсник, внутри которого имеются резистивные и реактивные элементы (Рис. 19.1 а).
К входу этого двухполюсника подключим источник синусоидальной ЭДС. Пусть при этом у нас есть возможность измерять амплитуду, начальную фазу и частоту напряжения и тока на входе (Рис. 19.1 б).
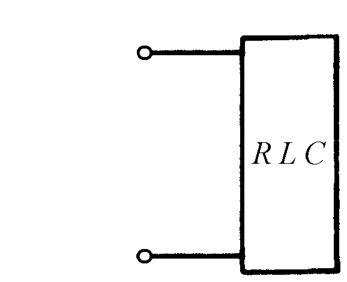
а)
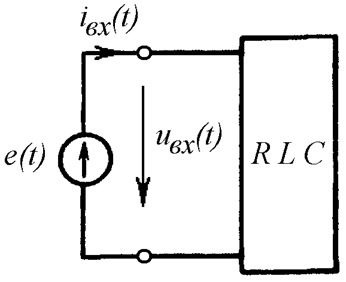
б)
Рис. 19.1
Итак, нам известно, что напряжение и ток на входе двухполюсника описываются следующими выражениями:
![]() , (19.1)
, (19.1)
![]() , (19.2)
, (19.2)
где ![]() –
начальная фаза напряжения,
–
начальная фаза напряжения,
![]() – начальная фаза тока.
– начальная фаза тока.
Чтобы определить мгновенную мощность, передаваемую в двухполюсник, достаточно перемножить (19.1) и (19.2):
![]() . (19.3)
. (19.3)
Преобразуем произведение двух синусоидальных функций в (19.3), воспользовавшись известной формулой:
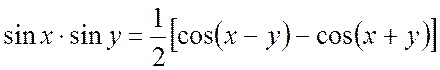 .
.
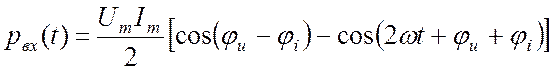 . (19.4)
. (19.4)
Разность ![]() в (19.4) это угол между напряжением и
током на входе двухполюсника. Обозначим его
в (19.4) это угол между напряжением и
током на входе двухполюсника. Обозначим его ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.