Электротехника \ Основы электротехники и электроники

Основы электротехники и электроники: Курс лекций, страница 12

Произведение  называется индуктивным сопротивлением и обозначается . Из (16.15) очевидно, что размерность индуктивного сопротивления – Ом:

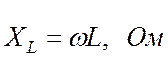                                                                       .             (16.16)

17*******

Мгновенная мощность на индуктивности:

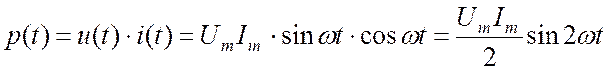                      .                                                                               (16.17)

18*******

На Рис. 16.3 представлены кривые тока, напряжения и мгновенной мощности на индуктивности.

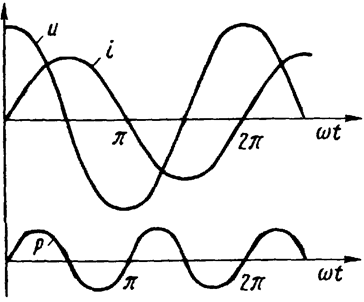
Рис. 16.3

Мгновенная мощность на индуктивности, проходя через ноль, с удвоенной частотой меняет знак. Это означает, что в первую четверть периода индуктивность потребляет энергию источника (запасает ее в магнитном поле), а во вторую четверть периода отдает запасенную энергию. Так как вся запасенная энергия, в конечном счете, возвращается обратно в источник, работу эта энергия не совершает. Поэтому мощность называется реактивной, а индуктивность называется реактивным элементом. Размерность реактивной мощности – Вольт-Ампер реактивный (ВАр).

Емкостной элемент (конденсатор) позволяет учесть накопление энергии в электрическом поле. Его характеризуют зависимостью заряда q от напряжения u (кулон-вольтной характеристикой) или емкостью. В линейных цепях емкость постоянна:

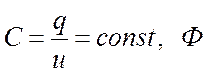                                                                   .          (16.18)

Размерность емкости – Фарада.

Если приложенное к конденсатору напряжение и не изменяется во времени, то заряд на его обкладках также не изменяется, и ток через конденсатор не проходит. Если же напряжение на конденсаторе изменяется во времени, например по синусоидальному закону:

                                                                      ,            (16.19)

то по синусоидальному закону будет меняться и заряд конденсатора:

                                                           ,  (16.20)

то есть конденсатор будет периодически перезаряжаться. Периодическая перезарядка конденсатора сопровождается протеканием через него зарядного тока:

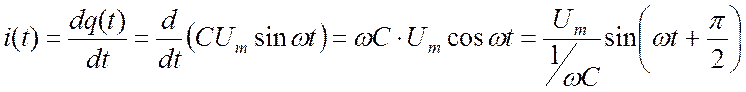.                                                                              (16.21)

Выражение (16.21) показывает, что на емкости кривая тока опережает кривую напряжения на угол . Таким образом, емкость также является фазосдвигающим элементом.

Дробь 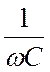 называется емкостным сопротивлением и обозначается . Размерность емкостного сопротивления – Ом:

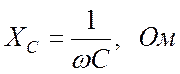                                                                      .            (16.22)

Мгновенная мощность на емкости:

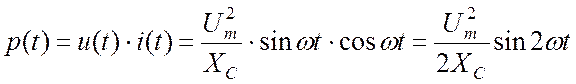                            .                                                                               (16.23)

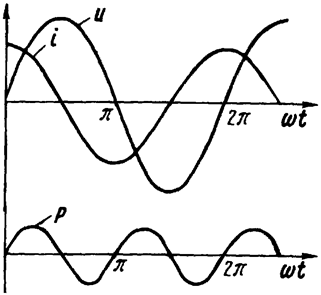
Рис. 16.4

На Рис. 16.4 представлены кривые тока, напряжения и мгновенной мощности на индуктивности. За первую четверть периода конденсатор потребляет от источника питания энергию, которая идет на создание электрического поля в нем. Во вторую четверть периода запасенная в электрическом поле энергия отдается источнику. Это также реактивная мощность, ее размерность – Вольт-Ампер реактивный (ВАр).

Ток через конденсатор равен:

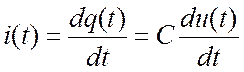                                                                .       (16.24)

Проинтегрировав (16.24), получим выражение для напряжения на конденсаторе:

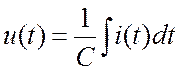                                                                      .            (16.25)

17. ВЕКТОРНЫЕ ДИАГРАММЫ

В линейных цепях синусоидального тока справедливы законы Кирхгофа для мгновенных значений токов и напряжений. Однако применение законов Кирхгофа непосредственно к гармоническим функциям весьма затруднительно. Одним из инструментов, облегчающих операции с гармоническими функциями, являются векторные диаграммы.

Как уже говорилось, любая синусоидальная функция, например, описывающая ток в цепи, характеризуется амплитудой, угловой частотой и начальной фазой:

                                                                  .          (17.1)

В некоторой системе координат построим вектор , модуль которого равен амплитуде , а угол между вектором и положительной полуосью ox равен начальной фазе  (Рис. 17.1 а).


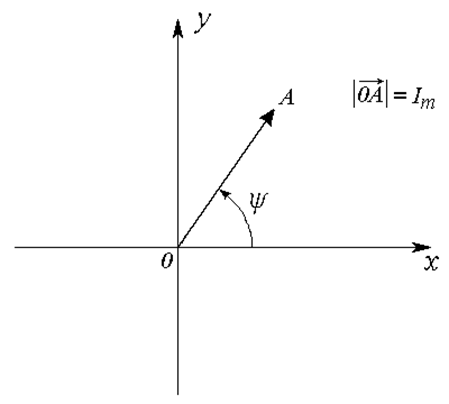
а)

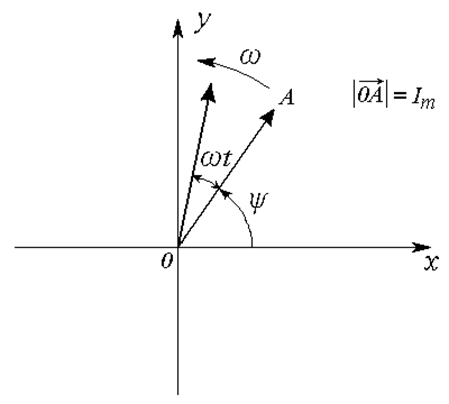
б)

Рис. 17.1

Начнем вращать вектор  относительно начала координат против часовой стрелки со скоростью . Через t секунд он передвинется на угол (Рис. 17.1 б).

Очевидно, что при вращении вектора  его проекция на ось oy будет тождественна гармонической функции (17.1). Значит, существует однозначное соответствие между вращающимся вектором  и током .

Как правило, в цепях действуют источники одной частоты. Поэтому векторы всех токов и напряжений будут вращаться с одной скоростью, и их взаимное положение не изменится. Следовательно, от операции сложения гармонических функций можно перейти к операции сложения векторов.

Так как при сложении и вычитании векторов имеет значение лишь их взаимная ориентация, нет необходимости вращать векторы. По этой же причине выбор системы координат и начала отсчета абсолютно произволен.

Примечание: Основной характеристикой синусоидальных токов и напряжений является действующее значение. Поэтому чаще всего в качестве длин векторов используют действующие, а не амплитудные значения токов и напряжений.

Пример 17.1

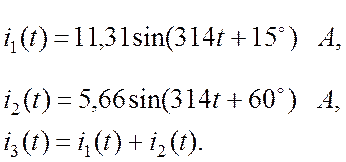
Определить ток .

Сложение синусоидальных функций осуществим с помощью векторной диаграммы для действующих значений токов.

Определяем действующие значения токов:

.

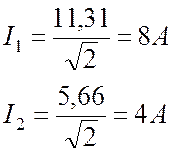Строим векторы I1 и I2. Векторы строятся из начала координат, их длины в заданном масштабе равны действующим значениям токов, а начальные фазы отсчитываются от положительной полуоси ox (Рис. 17.2 а).

Складываем векторы методом параллелограмма (Рис. 17.2 б).


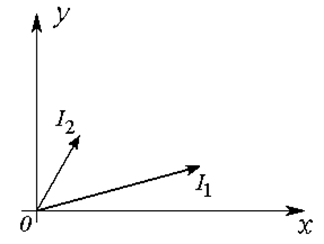
а)

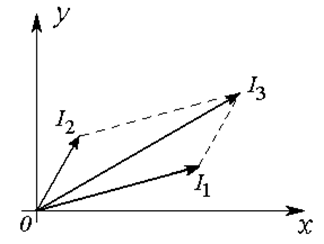
б)

Рис. 17.2

Из векторной диаграммы находим действующее значение тока I3 и начальную фазу ψ3:

.

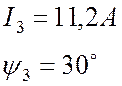Умножаем действующее значение тока I3 на  и находим амплитуду.

Окончательное решение имеет вид:

.

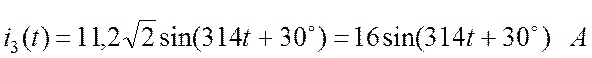18. СИМВОЛИЧЕСКИЙ МЕТОД

Скачать файл