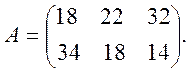Матричные игры: Методические указания к выполнению индивидуальных домашних заданий по курсу "Экономико-математические методы", страница 6

                                                  (11)

2. Пусть − доля имеющейся у агрофирмы пашни, засеянная культурой А, а − доля имеющейся у агрофирмы пашни, засеянная культурой В. Если  считать, что будет засеяна вся площадь, то  , , т.е. вектор  задает смешанную стратегию агрофирмы. Пусть − вероятность засушливого лета, − вероятность нормального лета, − вероятность дождливого лета. Тогда вектор  задает смешанную стратегию природы. Обозначим через  ожидаемую выручку агрофирмы с одного га пашни при применении ей своей смешанной стратегии.  Найдем оптимальные смешанные стратегии агрофирмы и природы и цену игры. В отличие от задач 1 и 2 рассмотрим еще один способ решения матричных игр − сведение задач теории игр к задачам линейного программирования. Опишем сначала процедуру сведения в общем виде.

Рассмотрим игру, определяемую матрицей

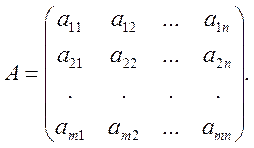
Утверждение 4. Для того, чтобы число  было ценой игры, а векторы  и  − оптимальными смешанными стратегиями первого и второго игроков соответственно необходимо и достаточно выполнение неравенств

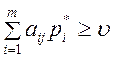
 ,                                            (12)

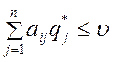
 .                                             (13)

Согласно утверждению 4 для оптимальной стратегии первого игрока должно  выполняться неравенство (12). Предположим для определенности, что   . Этого всегда можно добиться, прибавив ко всем элементам матрицы   одно и то же число . Подобная операция не изменит оптимальных стратегий игроков, а только увеличит цену игры на .  

Разделим обе части неравенства (12) на   (так как , то знак неравенства сохраняется):

,  .

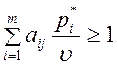Положим , тогда

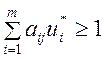,  .                                     (14)

Кроме того, так как по определению смешанных стратегий ,, то и ,. Сумма компонент вектора смешанных стратегий, согласно (5), должна быть равна 1:

            

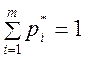
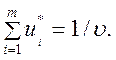
Так как первый игрок стремится получить максимальный  в среднем выигрыш, то он должен минимизировать величину . Учитывая это, а также (14), получаем, что для нахождения оптимальной смешанной стратегии первого игрока необходимо решить задачу линейного программирования:

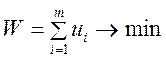
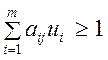,                                              (15)

,  .

Аналогично можно показать, что для нахождения оптимальной смешанной стратегии второго игрока необходимо решить задачу линейного программирования:

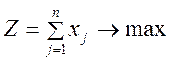
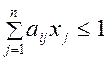,                                              (16)

,  .

Здесь , , где   − вектор смешанных стратегий второго игрока.

Заметим, что задача (15) является двойственной к задаче (16). Поэтому для того, чтобы найти решение матричной игры, необходимо найти оптимальное решение пары двойственных задач (15) и (16). Пусть  − оптимальное решение задачи (16),   − оптимальное решение задачи (15),  − оптимальные значения целевых функций.  Формулы для определения оптимальных стратегий и цены игры имеют вид:

      ,  ,     ,   ,     .             (17)

Теперь выпишем задачи линейного программирования, соответствующие игре, описываемой матрицей (11).

Задача агрофирмы	Задача природы

Найдем оптимальное решение каждой из этих задач.  Задача агрофирмы имеет две переменные, поэтому ее можно решить графически.  На рисунке 3.1 представлено графическое решение задачи агрофирмы.

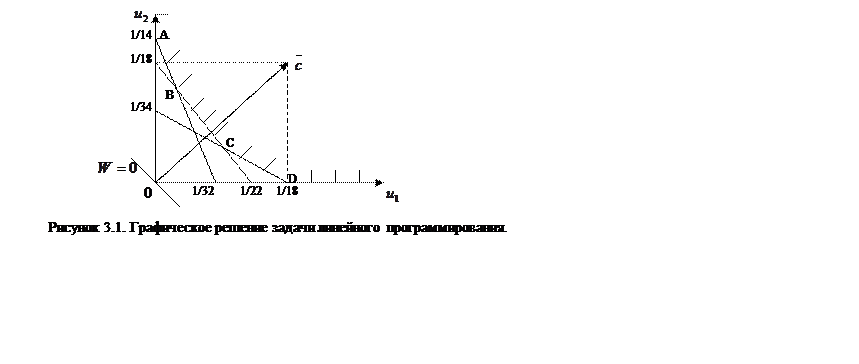
Область допустимых решений задачи на рисунке 3.1 представлена неограниченным четырехугольником ABCD, вектор  дает направление вектора-градиента целевой функции, линия  изображает линию уровня целевой функции. Точкой минимума является точка C, лежащая на пересечении первой и второй граничной прямых. Ее координаты найдем, решив систему уравнений:

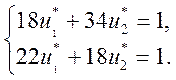
Отсю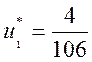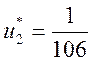да , . Тогда  .

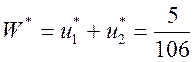Оптимальное решение задачи природы найдем, используя условия «дополняющей нежесткости».

Первая группа условий: x_jv_j=0, , где      

v₁ =,                          

v₂  =,         

v₃ =.

 Тогда

                              ,

                                ,

                           .

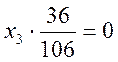
  Вторая группа условий:   где

Тогда

,

  .

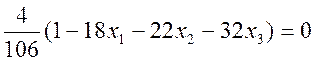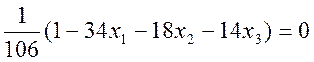  Отсюда получаем

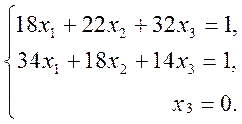
Решение этой системы:   .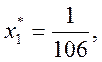

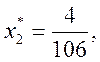
Далее, используя найденные оптимальные решения пары двойственных задач, по формулам (17) найдем цену игры и оптимальные смешанные стратегии игроков.

  

 

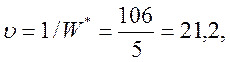
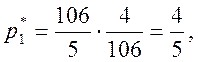
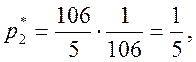
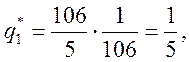
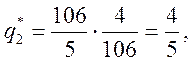
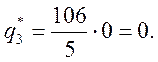
Таким образом, оптимальная смешанная стратегия агрофирмы равна . Это означает, что для получения максимальной ожидаемой выручки агрофирме необходимо 80% площади имеющейся пашни засеять культурой А и 20 %  пашни засеять культурой В. Ожидаемая выручка при этом должна составить  21,2 тыс. руб./га.

            Оптимальная смешанная стратегия природы  т. е. наиболее неблагоприятной для фирмы погодой будет − с вероятностью 20%  засушливое лето, с вероятностью 80%  нормальное лето, а дождливое лето − с вероятностью 0.

Литература

1. Акулич И. Л. Математическое программирование в примерах и задачах: Учеб. Пособие для студентов эконом. спец. вузов. – М.: Высш. шк., 1986.
2. Барабаш С. Б., Воронович Н. В. Экономико-математические методы. Учебное пособие. – Н.: НГАЭиУ. 2004.
3. Замков О. О., Толстопятенко А. В., Черемных Ю. Н. Математические методы в экономике. – М.: МГУ им. М. В. Ломоносова, изд-во «ДИС», 1998.
4. Экономико-математические методы и прикладные модели, под ред. В. В. Федосеева. – М.: Юнити, 2000.

Матричные игры

Методические указания

к выполнению индивидуальных домашних заданий

Подписано к печати                                2005г.