Матричные игры: Методические указания к выполнению индивидуальных домашних заданий по курсу "Экономико-математические методы", страница 3

Предположим, что игра является многоходовой, т. е. состоит из многих партий. Тогда каждый игрок будет в разных партиях применять свои  разные чистые стратегии, причем одни из них чаще, а другие − реже.

Смешанной стратегией первого игрока называется вектор , каждая компонента  ()  которого − это вероятность применения первым игроком его i-й чистой стратегии в многоходовой игре.

Из определения смешанной стратегии следует, что компоненты вектора p удовлетворяют следующим соотношениям:

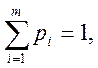
                                            (5)

Аналогично определяется смешанная стратегия второго игрока. Смешанной стратегией второго игрока называется вектор , каждая компонента , ,  которого − это вероятность применения вторым игроком его j-й чистой стратегии в многоходовой игре.  Компоненты вектора qудовлетворяют условиям:

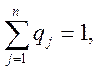
                                            (6)

Заметим, что чистые стратегии игроков являются частным случаем его смешанных стратегий. Например, i -я чистая стратегия игрока может быть представлена в виде такой смешанной стратегии, у которой i–я компонента равна 1, а все остальные  − 0.

Если игроки используют свои смешанные стратегии, то функция

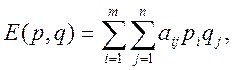                                                 (7)

называется платежной функцией.

Стратегия игрока называется оптимальной, если при многократном повторении игры она обеспечивает игроку максимально возможный средний выигрыш (минимально возможный средний проигрыш).

            Первый игрок стремится максимизировать свой гарантированный выигрыш , который определяется из условия:

Поэтому оптимальная смешанная стратегия первого игрока  является решением следующей задачи:

.

Второй игрок стремится минимизировать свой возможный наибольший проигрыш  при выборе стратегии , который определяется из условия:

Поэтому оптимальная смешанная стратегия второго игрока  является решением следующей задачи:

.

Если и  − оптимальные смешанные стратегии игроков, то число

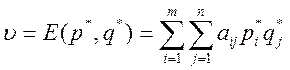                                              (8)

называется ценой игры.

Утверждение 2. Любая матричная игра имеет оптимальное решение в смешанных стратегиях.

Методические указания

Задача 1.  Графическое решение матричных игр.

1. Найдем оптимальные стратегии игроков в игре, заданной платежной матрицей

.

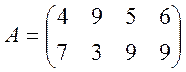Сначала проверим, есть ли в данной игре седловая точка.

Нижняя цена игры  равна max {4, 3} = 4.

Верхняя цена этой игры равна min {7, 9, 9, 9} = 7.

Поскольку , то  седловой точки у данной   игры нет, и решение нужно искать в смешанных стратегиях.

Графически решаются те матричные игры, в которых хотя бы у одного из игроков есть лишь две чистые стратегии. Задача именно этого игрока и решается графически. В задаче 1 у первого игрока две чистых стратегии, а у второго − четыре, поэтому будем решать графически задачу первого игрока. 

Смешанная стратегия первого игрока задается вектором . Построения осуществляются следующим образом. На горизонтальной прямой откладывается отрезок единичной длины, характеризующий вероятность  применения чистых стратегий первым игроком. Каждой точке этого отрезка сопоставляется смешанная стратегия первого игрока по следующему правилу: расстояние от точки до правого конца отрезка задает величину , а расстояние до левого его конца − величину  (см. рисунок 1.1).  Для определенных таким образом величин и  выполняются соотношения  , , поэтому, согласно (5), вектор  задает смешанные стратегии первого игрока.

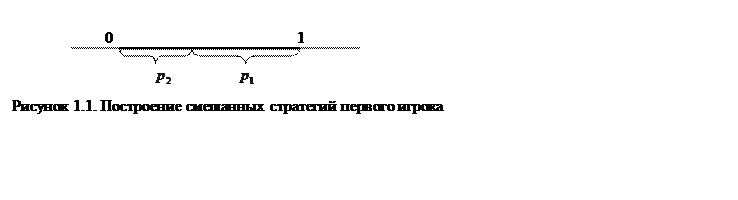
Тогда точка 0 задает вектор (1, 0), т. е. первую чистую стратегию первого игрока, а точка 1 задает вектор (0, 1), т. е. вторую чистую стратегию первого игрока. Далее через концы единичного отрезка проводятся вертикальные линии. На этих линиях откладываются выигрыши первого игрока при применении вторым игроком его различных чистых стратегий.  При этом выигрыши в случае применения первым игроком его первой чистой стратегии располагаются на левой вертикальной линии, а соответствующие второй чистой стратегии первого игрока − на правой вертикали. Точки левой и правой вертикали, соответствующие одной и той же чистой стратегии второго игрока, соединяются отрезками. На рисунке 1.2 изображены выигрыши первого игрока при применении вторым игроком первой чистой стратегии.  Римскими цифрами указано, что второй игрок применяет именно первую чистую стратегию.

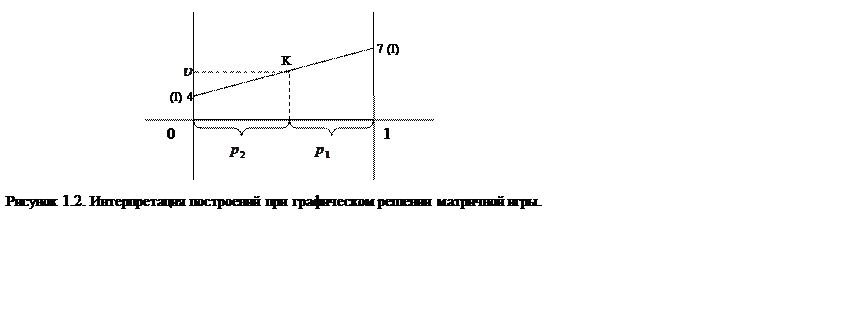
Любая точка K этого отрезка с координатами   и  показывает, что если первый игрок будет применять свою смешанную стратегию , а второй игрок − свою первую чистую стратегию, то средний выигрыш первого игрока будет равен . 

            Аналогичные построения выполняются для остальных чистых стратегий второго игрока (рисунок 1.3). Римские цифры указывают на номер  его чистой стратегии.

 

Жирным шрифтом выделена ломаная, соответствующая нижней границе выигрыша первого игрока, т.е. дающая его средний гарантированный выигрыш.  В точке М находится наибольший гарантированный выигрыш первого игрока (так как М − наивысшая точка ломаной). Эта точка является  пересечением отрезков, соответствующих первой и второй  чистым стратегиям второго игрока. Эти стратегии называются активными. Второй игрок будет использовать их в своей оптимальной смешанной стратегии с ненулевой вероятностью. Отрезки, соответствующие третьей и четвертой чистым стратегиям второго игрока, не проходят через точку М, поэтому эти стратегии в оптимальную смешанную стратегию второго игрока войдут с нулевыми вероятностями, так как их реализация приведет к большему проигрышу второго игрока. Такие стратегии называют пассивными.

            При определении оптимальной смешанной стратегии первого игрока и цены игры используется следующее утверждение:

Утверждение 3.  Если один из игроков применяет свои оптимальные смешанные стратегии, то его выигрыш будет равен цене игры, независимо от того, с какими вероятностями применяет другой игрок свои стратегии, вошедшие в оптимальную смешанную стратегию.