Матричные игры: Методические указания к выполнению индивидуальных домашних заданий по курсу "Экономико-математические методы", страница 2

Количественная оценка результатов игры называется платежом или выигрышем того или иного игрока. Соответствие между возможным набором возникающих в игре ситуаций и выигрышем игрока в каждой из этих ситуаций называется функцией выигрыша или платежной функцией.

Итак, формальное описание игры должно включать:

1)  перечень игроков;

2)  список стратегий каждого игрока;

3)  описание функций выигрыша каждого игрока.

Различные виды игр можно классифицировать, основываясь на разных принципах: по числу игроков, по числу стратегий, по свойствам функций выигрыша, по возможности предварительных переговоров и взаимодействий между игроками в ходе игры.

В зависимости от числа игроков выделяют игры  двух, трех и т.д. лиц. Возможны игры с бесконечным количеством игроков.

По количеству стратегий выделяют конечные и бесконечные игры. В конечных играх игроки располагают конечным числом стратегий (например, при игре в орлянку игроки могут выбрать «орла» или «решку», т.е., имеют по две стратегии).  Стратегии в конечных играх часто называют чистыми стратегиями (смысл этого специального термина будет понятен позже). В бесконечных играх игроки имеют бесконечное число возможных стратегий. Например, в игре «Продавец-Покупатель» каждый из них может назвать любую устраивающую его цену и количество продаваемого или покупаемого товара.

С точки зрения свойств платежных функций важным классом являются так называемые антагонистические игры, или игры с нулевой суммой. Игра называется игрой с нулевой суммой, если выигрыш одного игрока равен проигрышу другого.  Возможны также ситуации, когда игроки и выигрывают, и проигрывают одновременно, так что им выгодно действовать сообща.  Такие игры называются играми с постоянной разностью. Кроме того, существуют игры с ненулевой суммой, в которых есть и конфликты, и совместные действия игроков.

В дальнейшем мы будем рассматривать конечные игры двух лиц с нулевой суммой.

Итак, пусть есть два игрока, первый из которых имеет m возможных чистых стратегий, а второй − n чистых стратегий. Пусть при выборе первым игроком некоторой i-й стратегии , а вторым игроком j–й стратегии   первый игрок получает выигрыш, равный , а второй игрок эту величину проигрывает. Заметим, что в данном предположении нет какой-либо дискриминации по отношению ко второму игроку. Если величина  отрицательна, то первый игрок получает отрицательный выигрыш, т.е. проигрывает, а второй игрок при этом выигрывает. Из величин  составим матрицу, строки которой будут соответствовать чистым стратегиям первого игрока, а столбцы − чистым стратегиям второго игрока:

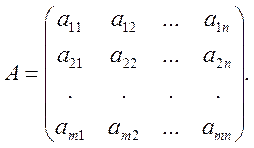                                            (1)

 Матрица A называется платежной матрицей.  Используя подобное представление конечных игр двух лиц с нулевой суммой, их часто называют матричными играми.

Например, при игре в «орлянку» каждый из игроков имеет по две стратегии: выбрать «орла» или «решку». Если игроки выбирают одинаковые стратегии, то первый игрок выигрывает 1 рубль, а второй игрок этот рубль проигрывает.  Если игроки выбрали разные стратегии (т.е. один из них выбрал «орла», а другой − «решку»), то первый игрок проигрывает 1 рубль, а второй выигрывает 1 рубль. Тогда платежная матрица имеет вид:

	Стратегии второго игрока		Стратегии первого игрока
	«Орел»	«Решка»
A = (	1	-1	)	«Орел»
	-1	1		«Решка»

В теории матричных игр предполагается, что каждый игрок знает не только свою функцию выигрыша и набор допустимых стратегий, но и функции выигрыша и стратегии всех остальных игроков.

Основным предположением теории игр является то, что каждый игрок стремится обеспечить себе максимально возможный выигрыш для любого действия противника. Пусть первый игрок считает, что какую бы стратегию он не выбрал, второй игрок выберет стратегию, минимизирующую свой проигрыш, т.е. минимизирующую выигрыш первого игрока. Тогда первый игрок стремится выбрать такую свою стратегию, которая даст ему наибольший выигрыш среди минимальных при каждой его стратегии.

Число

                                               (2)

называется нижней ценой игры, или максимином, а соответствующая ему чистая стратегия − максиминной.

Максиминная стратегия первого игрока обеспечивает ему наибольший гарантированный выигрыш.

Второй игрок также стремится выбрать такую стратегию, при которой его возможный максимальный проигрыш будет наименьшим.

Число

                                               (3)

называется верхней  ценой игры, или минимаксом, а соответствующая ему чистая стратегия − минимаксной.

Минимаксная стратегия минимизирует возможный проигрыш второго игрока.

Утверждение 1.  Для любой матричной игры выполняется неравенство:

                                         .                                                      (4)

Игра, для которой , называется игрой с седловой точкой, а число  называется ценой игры.

Для игры с седловой точкой нахождение решения заключается в выборе максиминной стратегии первого игрока и минимаксной стратегии второго игрока.

Например, пусть игра задана платежной матрицей

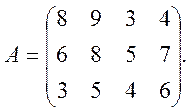
В этой игре у первого игрока есть три чистых стратегии, а у второго − четыре.

Нижняя цена этой игры равна max (3, 5, 3) = a₂₃= 5.

Верхняя цена этой игры равна min (8, 9, 5, 7) = a₂₃= 5.

Итак, , поэтому у игры есть седловая точка, поэтому  у нее  есть решение в чистых стратегиях. Максиминной стратегией первого игрока является его вторая чистая стратегия, а минимаксной стратегией второго игрока − его третья чистая стратегия. Цена игры равна 5.

Если матричная игра не имеет седловой  точки, то у нее нет решения в чистых стратегиях. В этом случае ее решение нужно искать в так называемых смешанных стратегиях, которые определяются следующим образом.