Векторная алгебра. Элементы аналитической геометрии, страница 4

3. Получаем формулу или уравнение, связывающее текущие координаты и какие-либо постоянные.

Подобный подход, повторяющийся от формулы к формуле, приводил к так называемым каноническим уравнениям (от слова канон – повтор).

7.2. Уравнения прямой на плоскости

1. Выведем уравнение прямой, проходящей через данную точку А(Х_а, Y_а) параллельно данному вектору l(m, n). Этот вектор называется направляющим для прямой L.

Дано: точка А(Х_а, Y_а), через которую проходит прямая L. Вектор l(m,n) || L

Найти: уравнение прямой L.

Решение: Сделаем чертеж (рис. 7.1).

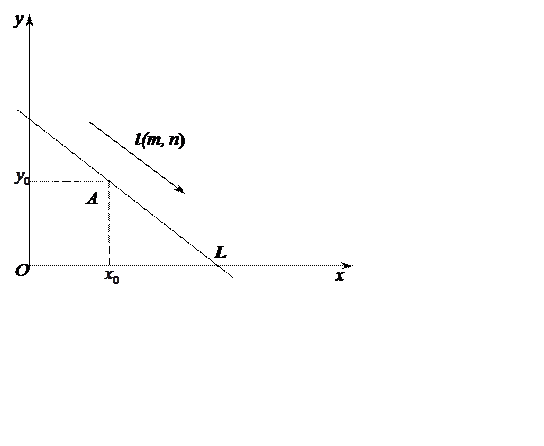Рис. 7.1

1. Берем текущую точку М (Х, Y) на прямой L.

2. Составляем вектор АМ (Х–Х_а, Y–Y_а).

Сравниваем векторы АМ и l. Они параллельны, следовательно, их координаты пропорциональны, т.е.

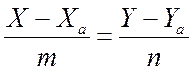,                                             (7.1)

Этомууравнению будут подчиняться только точки, лежащие на рассматриваемой прямой, и не будут удовлетворять точки, находящиеся вне ее. Именно это уравнение называют каноническим уравнением прямой.

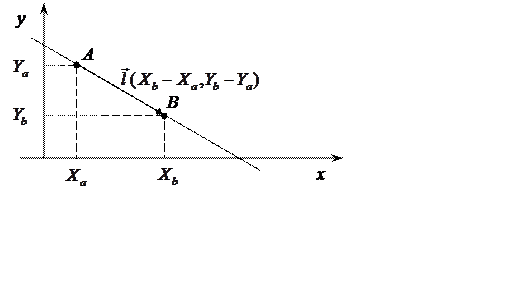Рис 7.2

Уравнение прямой, проходящей через две точки А (Х_а, Y_а) и В (Х_b,Y_b) составляется аналогично. В качестве направляющего вектора здесь берется вектор АВ (Х_в–Х_а , Y_b–Y_а) (рис. 7.2).

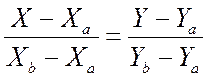.                                             (7.2)

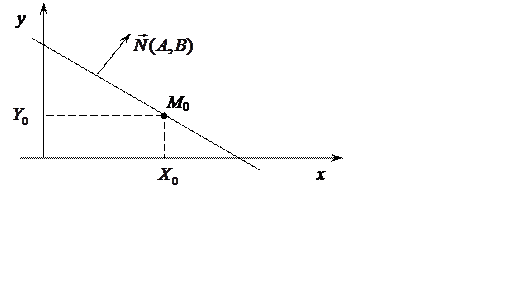
3. Уравнение прямой, проходящей через точку , перпендикулярно данному вектору N(A, B) (рис. 7.3).

Рис 7.3

Для вывода этого уравнения учитывается, что векторы N и  будут перпендикулярны и, следовательно, их скалярное произведение будет равно нулю. По формуле 6.6 из предыдущего параграфа составляем скалярное произведение в координатной форме и приравниваем его нулю:

.                                     (7.3)

Ему также будут отвечать только координаты точек, лежащих на прямой.

4. Уравнение прямой, проходящей через данную точку А (Х_а, Y_а) в заданном направлении.

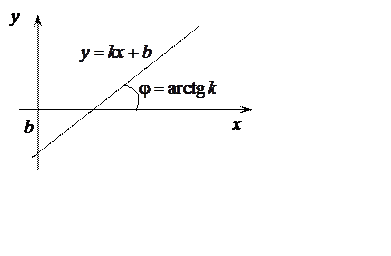Рис 7.4

Направление прямой можно задать с помощью углового коэффициента k, который равен тангенсу угла наклона прямой к положительному направлению оси ОХ ( рис.7.4). Тогда , где (Х, У) – координаты текущей точки. Разрешая это уравнение относительно , получим уравнение в виде:

.                                       (7.4)

5. Общее уравнение прямой на плоскости.

Если все предыдущие уравнения привести к общему знаменателю, раскрыть скобки и привести подобные члены, то в результате этих преобразований получим уравнение вида:

.                                       (7.5)

Оно называется общим уравнением прямой на плоскости. Чтобы убедиться, что такое уравнение описывает именно прямую, преобразуем его еще раз и запишем так:

.

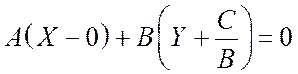– а это уравнение прямой, проходящей через точку (0, –С/В), перпендикулярно вектору с координатами (А, В), которое мы выводили.

Поэтому, любое уравнение первой степени относительно текущих координат описывает на плоскости прямую.

При решении задач по аналитической геометрии следует внимательно читать условие, которым задается прямая. Все остальное – дело техники.

Пример 7.1. Составить уравнение прямой, проходящей через точку
А(1, –3), параллельно вектору а(4, –7).

Решение. Воспользуемся уравнением 1, потому что именно в нем фигурирует точка и параллельный вектор. Получим:

,

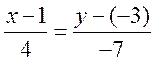что после приведения к общему знаменателю дает:

.

Раскрываем скобки, приводим подобные, получаем уравнение в общем виде:

.

Пример 7.2. Прямая проходит через точки А(3, 5) и В(4, 7). Будет ли точка K(1, 1) лежать на этой прямой?

Решение. Можно решить эту задачу чисто геометрически: построить точки А и В в Декартовой системе координат, соединить их прямой и посмотреть, будет ли точка K принадлежать этой прямой. А можно составить уравнение прямой, проходящей через две точки А и В, затем подставить в него координаты точки K и посмотреть, что получится. Если равенство – точка принадлежит прямой, если нет – не принадлежит.

Пойдем вторым путем. Уравнение прямой (АВ) будет составляться как уравнение прямой, проходящей через две точки:

,

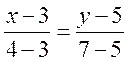или после приведения к общему знаменателю

, или .

Подставим в него K(1, 1), получим:

2(1 – 3)=(1 – 5), т.е. –4 = –4.

и это верно. Вывод: точка K принадлежит  прямой (АВ). Подкрепим свой вывод чертежом (рис. 7.5).

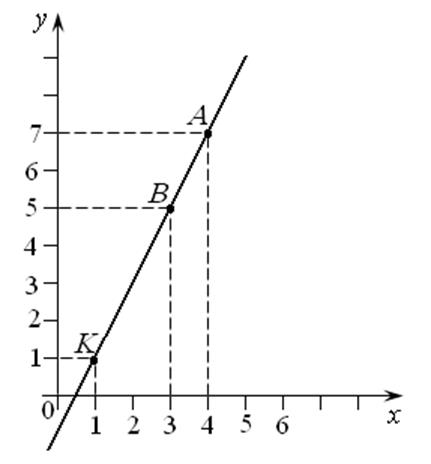
Рис. 7.5

Пример 7.3. Из точки M(3; 2) выходит луч света под углом  к оси OX. Найти уравнения падающего и отраженного лучей (рис. 7.6).

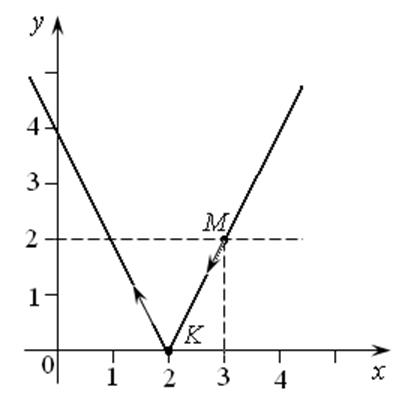
Рис. 7.5

Решение. Найдем уравнение падающего луча. Эта прямая L₁ проходит через точку M с угловым коэффициентом.

.

Тогда используя уравнение (7.4), получим

,

или

.

Это уравнение падающего луча. Чтобы составить уравнение отраженного луча L₂, нужно знать координаты точки отражения K и угловой коэффициент k₂. Координаты точки отражения K можно найти как точку пересечения прямой L₁ и оси Ox:

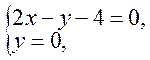             Þ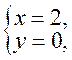               

т.е. K(2;0). Угловой коэффициент k₂ найдем из того условия, что «угол падения равен углу отражения». Тогда очевидно, что

.

Отсюда

.

Теперь известны все параметры, чтобы записать уравнение отраженного луча:

,

или

.

7.3. Взаимное расположение прямых на плоскости

Очень часто при решении задач по аналитической геометрии приходится выяснять, пересекаются прямые или нет, и если да – то в какой точке и под каким углом. Ответим на этот вопрос.

Пусть две прямые L и L заданы своими общими уравнениями:

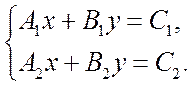                                                 (7.6)

Какую информацию несут коэффициенты  и ? Это координаты перпендикулярных (нормальных) векторов к обеим прямым (см. «уравнение прямой, проходящей через данную точку, перпендикулярно данному вектору»).

Для того чтобы определить, будут ли они пересекаться, нужно решить систему уравнений (7.6). Вспомните, когда система будет совместна и определена. Когда главный определитель отличен от нуля, т.е. когда его строки непропорциональны: 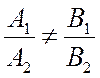. Тогда система будет иметь единственное решение, которое можно найти любым методом (Крамера, Гаусса и т.д.).