Векторная алгебра. Элементы аналитической геометрии, страница 2

Пример 6.3. Построить кривую  (двухлепестковая роза).

Решение. Составим таблицу и в соответствии с ней построим график (рис. 6.6).

№	1	2	3	4	5	6	7	8	9
j	0				p				2p
2j	0		p		2p		3p		4p
r	0	1	0	–1	0	1	0	–1	0

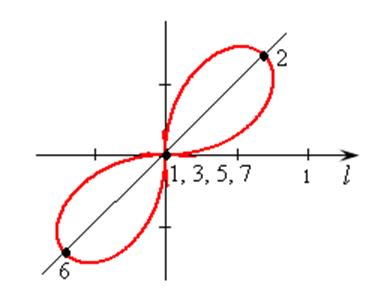
Рис. 6.6

Здесь те значения j, при которых , не рассматривались. Легко догадаться, что график , или , будет иметь k лепестков.

Связь между полярной и декартовой системами координат устанавливается просто, если совместить полюс и начало координат, полярную ось и ось абсцисс, и уравнять масштабы (рис. 6.7).

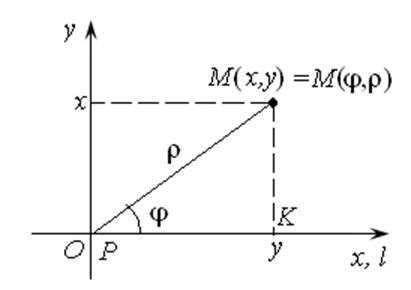
Рис. 6.7

В треугольнике OMK   , , тогда

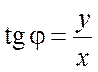 и .                                          (6.7)

Это два равенства выражают r и j через x и y. С другой стороны

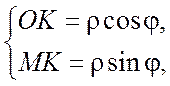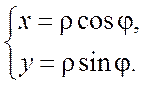    или                                     (6.8)

Эти два равенства выражают x и y  через  r и j.

Например, уравнение  в декартовой системе координат запишется так:

,

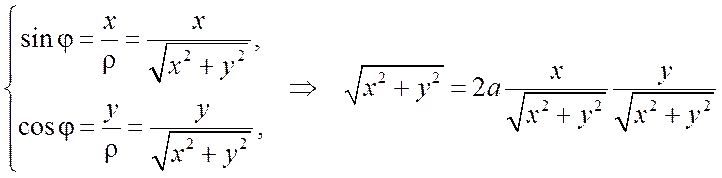или

,

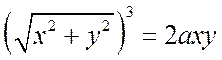т.е. в полярной системе оно имеет компактный вид. Мы будем переходить из системы в систему всегда, когда это облегчает какое-то действие.

6.4. Элементы векторной алгебры

Рассмотрим пространство векторов и основные действия с ними по той же цепочке «понятие – определение – действия», которую мы использовали и в матрицах, и в определителях.

Определение 6.1. Вектором называется направленный отрезок на плоскости.

Обозначается вектор одним из следующих способов: 1) двумя буквами, например,  или АВ или 2) одной буквой, например, , а. Длина вектора называется его модулем и обозначается, например,  или .

Множество векторов, с определенными над ними операциями, называется пространством векторов. Особую роль играют нуль-вектор и единичный вектор.

Нуль-вектор О – это вектор, модуль которого равен нулю, а направление неопределенно.

Единичный вектор е – это вектор, модуль которого равен единице, а направление произвольно.

Определение 6.2. Два вектора АВ и СD называются равными, если: 1) они параллельны, 2) их модули равны и 3) направления совпадают. Тогда пишут векторное равенство АВ = СDили.

Поскольку здесь не сказано, на каких именно параллельных прямых лежат эти векторы, можно взять любые, а, значит, перенос вектора параллельно самому себе не изменит его величины и направления. Этим обстоятельством пользуются достаточно широко, перенося векторы параллельно себе в любую точку не только плоскости, но и пространства.

Если первые два условия равенства векторов выполнены, а последнее – нет, векторы называются противоположными: АВ = –СD.

Если первое и третье условие выполнены – векторы называют параллельными или пропорциональными: АВ = kСD

Простейшие действия над векторами: сложение, вычитание, умножение на число, скалярное произведение двух векторов.

1. Для того чтобы найти сумму двух векторов а + b, нужно начало второго вектора совместить с концом первого и соединить начало первого с концом второго (правило большей диагонали (рис. 6.8)). Получившийся вектор будет называться суммой векторов .

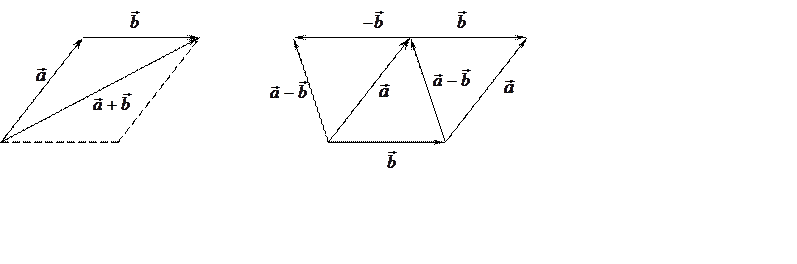Рис. 6.8                                                                        Рис. 6.9

Свойства суммы векторов:

1)  а+ b = b +а,

2)  а+ 0 = а,

3)  а+(–а) = 0,

4)  (а+в)+с = а+(в+с).

2. Разность векторов а – b можно ввести как сумму векторов а + (–b), (правило меньшей диагонали (рис. 6.9).

3. При умножении вектора на число k, его модуль меняется в |k| раз, направление остается прежним, если k > 0 , и меняется на противоположное, если k < 0.

4. Скалярным произведением двух векторов называется число (скаляр), равное произведению модулей этих векторов и косинуса угла между ними.

.                                            (6.9)

Свойства скалярного произведения:

1)  (а×b) = (b×а),

2)  (а×kb) = k(а×b),

3)  (а + b) с=а×с+ b×с,

4)  (а×0)=0,

5)  (а×b) = 0, если   а = 0, или   b = 0, или   cos(a,b) = 0.

После того, как векторы поместили в Декартову систему координат, потребовались еще два определения.

Определение 6.3. Проекциями вектора на ось ОХ и ось ОY называются разности соответствующих координат его начала и конца: , .

Чтобы показать отличие координат вектора от координат точек, Декарт предложил соотнести их с единичными векторами, лежащими на осях координат – i и j.

Определение 6.4. Произведение проекции вектора на единичный вектор называется составляющейвектора на ось:

,   .

С учетом всей информации вектор и его модуль можно описывать с помощью координат следующим образом:

                          (6.10)

– это выражение называется разложением вектора в базисе i, j;

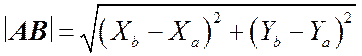                        (6.11)

– модуль вектора;

                              (6.12)

– вектор в координатной форме.

Эти три формулы однозначно определяют вектор в Декартовой системе координат. Именно они положили начало векторной алгебре.

Векторы i и j называются ортами. Их модули равны единице, они направлены в положительном направлении осей координат.

С введением декартовой системы координат все действия над векторами передались их представителям – координатам, то есть числам. Это очень облегчило жизнь. В новой трактовке основные определения стали звучать так:

Нуль-вектор – это вектор, координаты которого равны нулю 0 (0,0).

Два вектора равны, если равны их соответствующие координаты:

.

Для того чтобы сложить два вектора, нужно сложить их координаты. Это действие очень напоминает действие сложения матриц, где вектор – это матрица-строка, или матрица-столбец, записанные так:

а (а, b, с) + b (l, m, n) = (а+b) (а+l, b+m, с+n).                   (6.13)

Разность векторов, произведение вектора на число вводится аналогично: их координаты вычитаются и умножаются на число.