Параллельные векторы имеют пропорциональные координаты. Если а || b, то
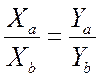, (6.14)
Скалярное произведение векторов, применяемое в физике для определения работы по перемещению веса Р в направлении вектора С равно числу – сумме произведений одноименных координат. Если Р(Хр, Yр), С(Хс, Yс), то
(Р·С) = Хр·Хс + Yр·Yс. (6.15)
Согласно первому определению скалярного произведения
(Р·С) = |P|·|C|·cos(P^C),
что в координатной форме запишется так:
(P·C)= |P|·|C| cos(P^C) = Xp·Xc + Yp·Yc. (6.16)
Из последней формулы по известному скалярному произведению и координат векторов легко можно найти угол между векторами:
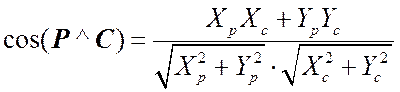. (6.17)
В обыденной жизни мы, конечно, пользуемся более легкими определениями. Но нужно ли забыть старые? «Кто отбрасывает прошлое – рискует потерять будущее». Кто-то из великих.
Пример 6.4. Стороны квадрата АВСD – суть векторы АВ, ВС, DА, DС. Найдите среди них равные и противоположные, если координаты точек А(1, 2), В(1, 4), С(З, 4). Сделать чертеж.
Решение.
Сделаем чертеж (рис. 6.10). На первый взгляд может показаться, что все четыре
вектора равны между собой, т.к. являются сторонами квадрата. Но это не так.
Вспомните первое определение равенства векторов. На параллельных прямых лежат
только векторы АВ и DС, АD и ВС. Но если первая пара направлена
в одну сторону, то вторая – в противоположные. Поэтому делаем вывод, что АВ
= DС, АD = –ВС. Такой же ответ получим, если
найдем координаты всех векторов. Так, АВ(1–1, 4–2) = (0, 2), DС(3 – 3, 4 – 2) = (0, 2), следовательно, второе определение
не противоречит первому. Вектор DА имеет
координаты (1–3, 2–2)= (–2, 0), ВС (3–1, 4–4) = (2, 0), т.е. они
противоположны. Этот ответ мы могли получить сразу, не делая чертежа. Модули
всех векторов равны 2.
Отнесенные в систему координат векторы были так просты в обращении, что их с удовольствием взяли на вооружение и экономисты. Такие понятия, как «вектор цен», «пространство товаров» уже ни у кого не вызывает удивления. Мы встречались с ними, когда выполняли работу по линейной алгебре
Пример 6.5. Первоначальные цены на товары пяти видов имели вид: 1-й стоил 120 руб., второй – 319 руб., третий – 276 руб. четвертый – 519 руб., пятый – 134 руб. Через год их цена установилась на следующих цифрах: 124, 187, 309, 564, 100 руб. Определить вектор цен.
Решение.
Для того, чтобы найти вектор цен, нужно найти их изменение. На языке экономики
– это прирост. Его находят вычитанием из конечной цифры предыдущую,
(Х
–Х
).
Поэтому получим:
С (124–120, 187–319, 309–276, 564–519, 100–120) = (4, –132, 33, 45, –20).
О чем говорят эти цифры, или координаты этого вектора? Цены на первый, третий, четвертый товары повысились, а на второй и пятый – понизились. Этот вектор называют еще вектором абсолютного прироста. Математик на этом бы остановился, но экономисту важен не сам прирост, а относительный прирост по отношению к первоначальному, да еще в процентах. Поэтому каждая координата последнего вектора делится на первоначальную цену соответствующего товара и умножается на 100%. Получим:
С% (4/124·100%, –132/319·100%, 33/276·100%, 45/519·100%, –20/100·100%) = = (3,22%, –41,38%, 11,96%, 8,67%, –20%).
Анализируя эти цифры, приходим к выводу, что наибольшее повышение получил третий товар, а наибольшее снижение – второй. Новый вектор называется вектором относительного прироста.
Так отвлеченное понятие «вектор» работает в экономике. Приложением его к технике, строительству и т.д. занимаются другие науки, рассмотрение которых выходит за рамки этого курса.
1. Оказалось, что декартова система координат – не единственная из возможных систем. Полярная система тоже описывает точку на плоскости с помощью пары чисел: угла j и расстояния r. Между системами существует связь и можно переходить из одной в другую.
2. Векторы определяются только в декартовой системе координат. Действия над векторами удобнее производить в координатной форме.
3. Векторы могут быть применены и в экономике: например, вектор цен.
На этом мы закончим знакомство с различными системами координат и в следующей лекции посмотрим, как описываются различные геометрические объекты с помощью формул.
Могущественна геометрия;
соединенная с искусством –,
неодолима.
Еврипид
ПЛАН
1. Введение.
2. Уравнение прямой на плоскости.
3. Взаимное расположение прямых
4. Определение кривой второго порядка.
5. Каноническое уравнение параболы.
6. Каноническое уравнение эллипса.
7. Каноническое уравнение гиперболы.
8. Приведение уравнения кривого порядка к каноническому виду.
9. Заключение.
Надо сказать, что после того как Декарт сообщил о своей системе координат, его открытие распространилось по Европе с быстротой пожара. Весь накопленный описательный материал прямых и кривых облекался в наряд формул. Больше всего оказалось уравнений, описывающих прямую линию, или просто прямую.
Новая система координат упростила жизнь не только физике. Геометрия, всегда считавшаяся привилегией мудрецов, тоже приобрела более понятный и наглядный вид.
Наука, описывающая геометрические фигуры с помощью формул, называется аналитической геометрией.
Самым простым геометрическим объектом является прямая линия.
Рассмотрим общий подход к составлению уравнений различных линий и поверхностей. В данном случае порядок действия будет такой:
1. Берем текущую точку М (х, у) рассматриваемого объекта. Текущие координаты (х, у) могут принимать любые, допустимые для объекта значения, т.е. не «соскакивать» с линии или поверхности.
2. Подставляем ее в уравнение связи для геометрического места точек. Уравнение связи, как правило, словесно описывает объект.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.