Основные понятия векторной алгебры. Проекция вектора на ось. Координаты вектора. Скалярное произведение векторов, страница 9

      Показать, что прямые, имеющие уравнения

и

совпадают.

Решение.

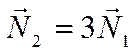       Векторы нормалей прямых равны , . Отсюда получаем  .  Следовательно, нормали колиинеарны, а прямые либо параллельны, либо совпадают. Непосредственной подстановкой в уравнение легко убедиться, что пара чисел   является решением обоих уравнений. Значит прямые совпадают так как имеют общую точку.

Пример.

      Показать, что прямые, имеющие уравнения

и

параллельны.

Решение.

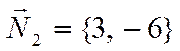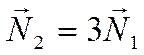       Векторы нормалей прямых равны   и  . Отсюда  следует, что и значит нормали коллинеарны. Следовательно, прямые либо совпадают, либо параллельны. Так как пара чисел   является решением первого уравнения и не является решением второго, то прямые параллельны.

         Если нормали прямых не коллинеарны, то прямые пересекаются в одной точке. Точку пересечения прямых в этом случае можно найти решив систему уравнений

.

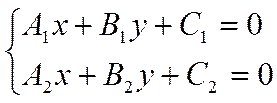Если пара чисел 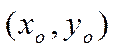 есть решение системы, то точка  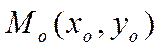есть точка пересечения прямых.

Пример.

        Найти точку пересечения прямых, заданных уравнениями

и

.

Решение.

          Решая систему уравнений

,

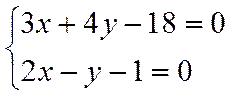находим, что пара чисел является решением системы. Следовательно, точка   есть точка пересечения прямых.

         Если прямые пересекаются, то можно поставить вопрос об угле под которым они пересекаются. При этом, если прямые пересекаются не под прямым углом, то можно говорить об остром и тупом угле между прямыми. Как видно

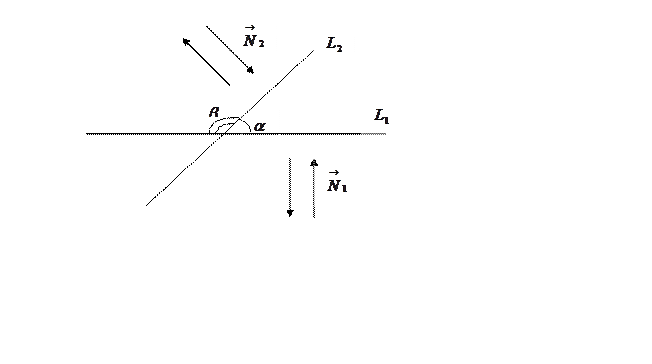
Рис. 39.

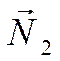из рисунка 39,  если векторы нормалей к прямым   и   образуют острый угол, то угол между ними равен острому углу между прямыми. Если же эти векторы образуют тупой угол, то угол между ними равен тупому углу между прямыми. Если прямые заданы уравнениями, то из уравнений можно найти координаты векторов   и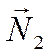. Тогда косинус угла   между этими векторами можно найти по формуле

.

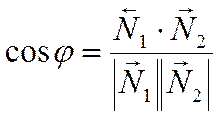При этом,  если , то угол между векторами равен

острому углу    между прямыми. Если же , то угол между векторами равен тупому углу между прямыми. Зная острый угол  между прямыми можно найти тупой угол  между прямыми и наоборот, так как углы  и   связаны соотношением   .

       Если задаться целью найти острый угол между прямыми, то для этого можно воспользоваться формулой

.

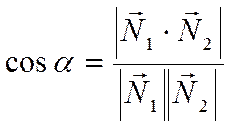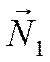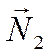В самом деле, если векторы  и образуют острый угол, то 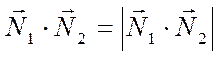 . В этом случае

.

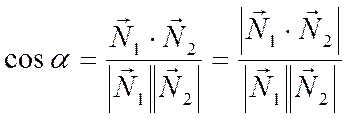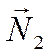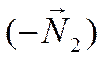Если же векторы   и   образуют тупой гол, то векторы  и  образуют острый угол, равный острому углу между прямыми. Тогда

.

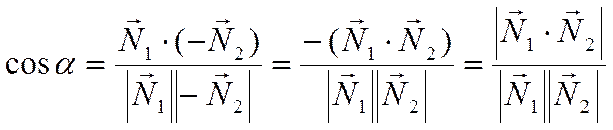Рассмотрим пример на нахождение угла между прямыми.

Пример.

         Найти острый угол между прямыми

и

.

Решение.  

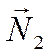         Векторы нормалей к прямым   и   равны

.

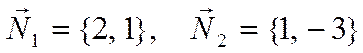Пусть - острый угол между прямыми. Тогда

.

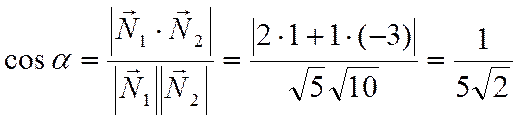Отсюда

.

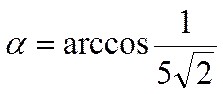§4. Расстояние от точки до прямой

      Получим формулу, выражающую расстояние от заданной точки до заданной прямой.

Рис. 40.

       Пусть на плоскости имеется прямая, заданная уравнением

и точка , не лежащая на этой прямой. Возьмем на прямой произвольную точку  (Рис. 40). Тогда расстояние от точки  до прямой, как видно из рисунка, равно

,

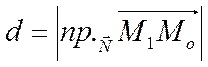где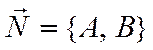 - нормаль к прямой. Используя полученную

выше формулу для проекции вектора на вектор

,

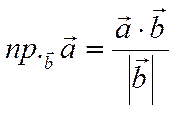получаем

.

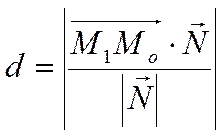Так как

,

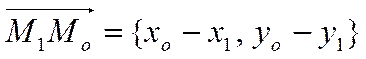то

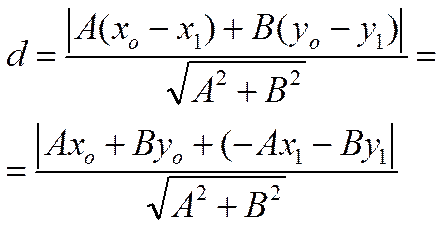
Поскольку точка   лежит на прямой, то

есть верное числовое равенство. Отсюда

.

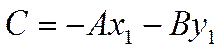Тогда, с учетом этого, для расстояния  получаем формулу

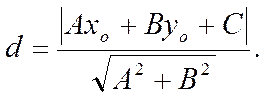
§5. Уравнение прямой с угловым коэффициентом

         Как установлено выше, уравнение любой прямой на плоскости можно записать в виде

.

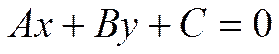Ниже, в этом параграфе будем рассматривать только такие прямые, в уравнении которых  . Множество этих прямых включает все прямые на плоскости за исключением прямых, параллельных оси и прямой, совпадающей с осью .  В самом деле, если  , то вектор нормали к прямой  коллинеарен орту оси  вектору 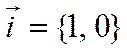 и значит прямая перпендикулярна оси .

       Если  , то обе части уравнения

можно разделить на  . Тогда получаем

,

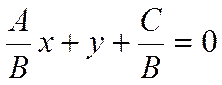или

.

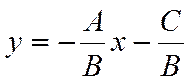Обозначим

.

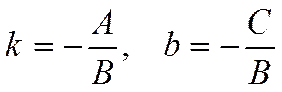Уравнение прямой принимает вид

 .

Итак, уравнение любой не вертикальной прямой можно записать в виде

,

где  и   -фиксированные числа.  Параметр   называется угловым коэффициентом прямой. Уравнение прямой, записанное в таком виде, называется уравнением прямой с угловым коэффициентом.

Пример.

       Уравнение прямой имеет вид

.

Записать уравнение этой прямой в виде уравнения прямой с угловым коэффициентом.

Решение.

      Разделив обе части уравнения на , получим после элементарных преобразований

.

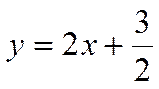          Ниже вводится понятие угла наклона прямой.

Определение.

       Пусть прямая на плоскости не параллельна оси  и пересекает ось  в точке  (Рис. 41). Углом наклона прямой называется угол, на который надо повернуть ось  вокруг точки   против часовой стрелки до совмещения с

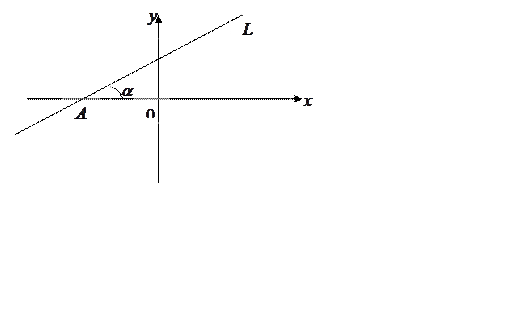
                                               Рис. 41.

прямой. Если прямая параллельна оси , то по определению полагаем, что угол наклона прямой равен нулю. Угол наклона прямой заключен в пределах

.

          Пусть прямая задана уравнением с угловым коэффициентом.  Сформулируем в виде теоремы утверждение о связи углового коэффициента с углом наклона прямой.

 Теорема.

Пусть прямая задана уравнением

.

Пусть -  угол наклона прямой. Тогда справедливо равенство

.

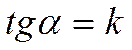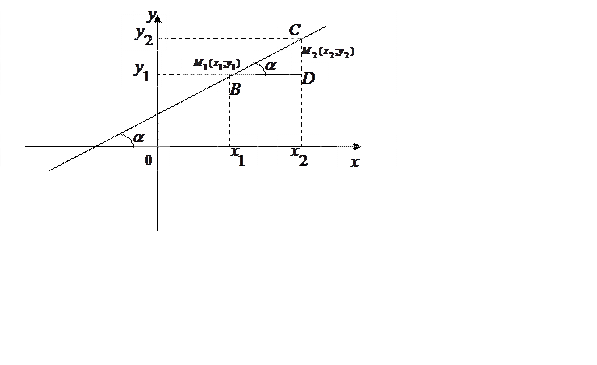
Рис. 42.

Доказательство.

        Заметим, что так как прямая не вертикальная, то  и значит  определен. Рассмотрим сначала случай (Рис. 42), когда угол наклона острый, т.е.

.

Возьмем на прямой две точки   и    как это показано на рисунке 42. Тогда в прямоугольном треугольнике  длины катетов равны следующим значениям

.

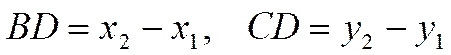Следовательно

.

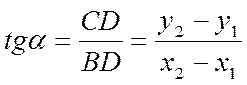Так как точки  и   лежат на прямой, то

.

Отсюда

.

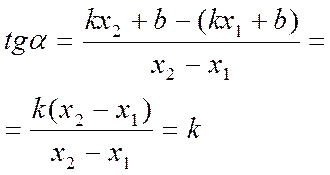Рассмотрим теперь случай (Рис. 43), когда

.

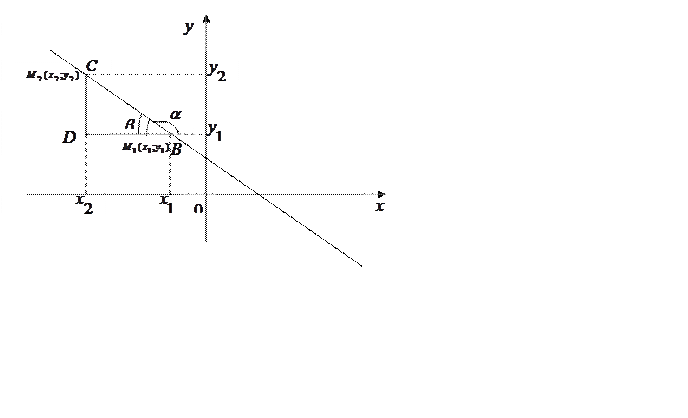
Рис. 43.