Основные понятия векторной алгебры. Проекция вектора на ось. Координаты вектора. Скалярное произведение векторов, страница 6

        Пусть даны три вектора ,  и  . Смешанным произведением векторов  ,  и  называется число, обозначаемое 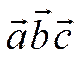  и определяемое равенством

.

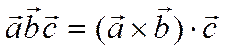Свойства смешанного произведения векторов.

Свойство 1.

      Если

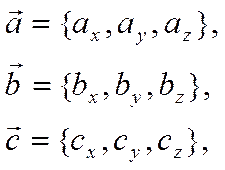
То

.

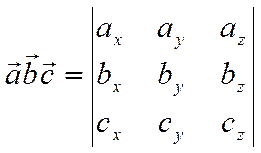Это свойство смешанного произведения следует непосредственно из свойств векторного и скалярного произведения векторов:

.

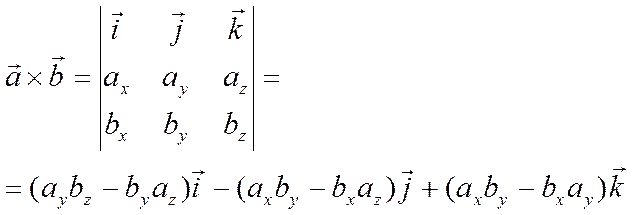
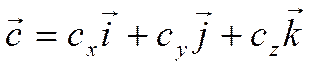Следовательно

.

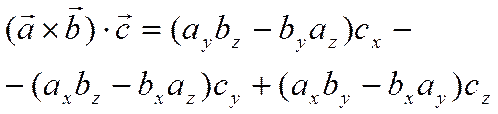С другой стороны, если разложить определитель

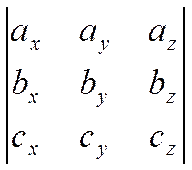
по третьей строке, то получим

.

Таким образом, смешанное произведение 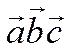 можно представить указанным определителем.

Свойство 2.

.

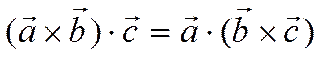Это свойство следует непосредственно из выражений векторного и скалярного произведений через координаты векторов и доказывается так же как и свойство 1.

Свойство 3.

,

т. е. при перестановке двух любых сомножителей смешанное произведение меняет знак. Это свойство проверяется непосредственно с помощью свойства 1.

Свойство 4.

      Для того, чтобы векторы ,  и   были компланарны необходимо и достаточно, чтобы выполнялось равенство

.

Докажем это свойство.

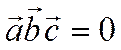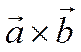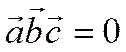       Пусть векторы ,   и  ненулевые и лежат в одной плоскости, т.е. компланарны. Покажем, что . В самом деле, вектор  перпендикулярен плоскости, в которой лежат векторы  и  , значит перпендикулярен вектору  , так как он также лежит в этой плоскости. Следовательно . Обратно, пусть . Если , и ненулевые векторы и 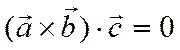, то вектор  перпендикулярен 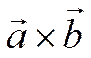. Кроме того, вектор перпендикулярен вектору 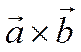 и вектор перпендикулярен вектору 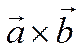 . Следовательно, все три вектора ,  и   перпендикулярны одному и тому же вектору  и значит лежат в одной и той же плоскости (будучи отложенными от общей точки).

       Из последнего свойства в частности следует, что если какие-то два из тройки векторов ,   и  коллинеарны, то , так как в этом случае векторы , и компланарны.

       Введем понятие параллелепипеда, построенного на тройке векторов.

Определение.

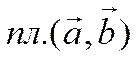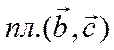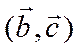       Пусть ненулевые векторы ,  и некомпланарны. Отложим их от общей точки. Обозначим , ,   плоскости, в которых лежат пары векторов ,  и , соответственно. Через конец вектора проведем плоскость, параллельную , через конец вектора проведем плоскость, параллельную плоскости , через конец вектора проведем плоскость, параллельную плоскости . Тогда,  ,  ,  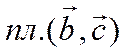 и построенные

Рис. 30.

плоскости ограничивают параллелепипед . Этот параллелепипед называется параллелепипедом, построенном на векторах , и . Теперь сформулируем свойство 5 смешанного произведения.

Свойство 5.

         Если тройка векторов  правая, то

,

если же тройка левая, то

,

где   - объем параллелепипеда, построенного на векторах , и  . Докажем это свойство.

      Пусть-правая тройка векторов. По определению

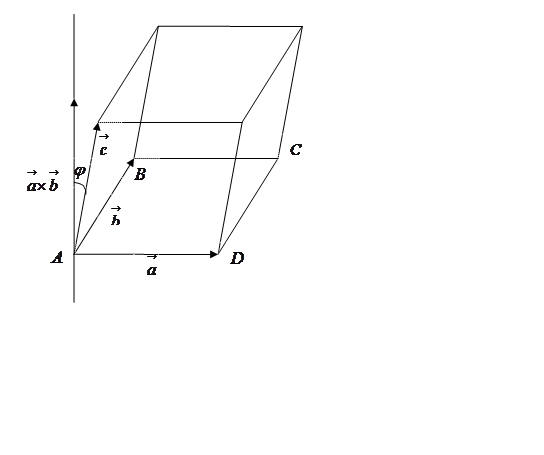
Рис. 31.

.

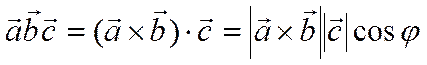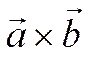где - угол между векторами  и . Построим на векторах  , и  параллелепипед  (Рис. 31). Объем этого параллелепипеда равен

,

где  - площадь основания , - высота параллелепипеда. Так как  параллелограмм, то

.

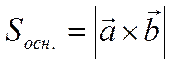Высота в  случае, когда  правая тройка, как видно из рисунка , равна

.

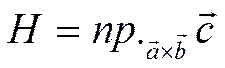Следовательно, учитывая, что

,

получаем

,

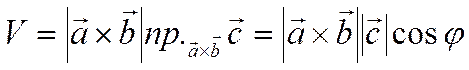где - угол между векторами   и . Таким образом,

.

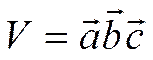           Пусть теперь  - левая тройка векторов. Построим параллелепипед на векторах , и . Как видно

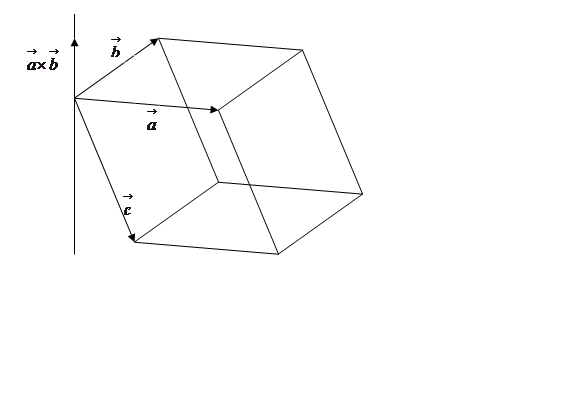
Рис. 32.

из  рисунка 32, в этом случае

,

где - угол между векторами и , причем угол  в этом случае тупой и значит  отрицателен. Следовательно, в случае левой тройки векторов

.

Замечание.

         Независимо от того, является ли тройка векторов  правой или левой,  объем параллелограмма, построенного на этих векторах, равен

.

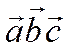В самом деле, если - правая тройка  неотрицательное число и значит

.

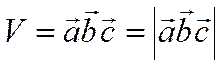В случае, когда 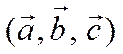 левая тройка, число  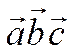отрицательно и. следовательно,

.

        Пусть имеется тройка ненулевых некомпланарных векторов  ,  и . Отложим их от общей точки. Если

Рис. 33.

Концы векторов соединить отрезками, как это показано на рисунке 33, то получим треугольную пирамиду. Эта пирамида называется пирамидой, построенной на векторах, и .

В элементарной геометрии доказывается, что объем этой пирамиды 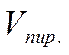  равен одной шестой объема параллелепипеда, построенного на векторах  , и . Отсюда следует, что объем пирамиды равен

.

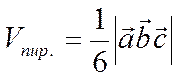      Рассмотрим пример на свойство 4.

Пример.

    Доказать, что точки ,  , и  лежат в одной плоскости.

Решение.

     Точки  лежат в одной плоскости тогда и только тогда, когда векторы  компланарны. Покажем, что выполнено условие компланарности (свойство 4)

.

Найдем координаты векторов

Тогда, согласно свойству 1

.

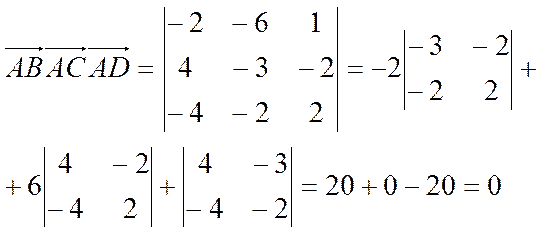Следовательно, векторы 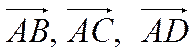 коллинеарны (лежат в одной плоскости), а значит точки   лежат в одной плоскости.

Глава 2. Прямая на плоскости

§1. Уравнение прямой на плоскости, проходящей через заданную точку и перпендикулярной заданному вектору  

Определение.

         Уравнением с двумя неизвестными называется выражение вида

.

Например

.

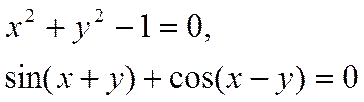Определим понятие решения уравнения рассмотренного вида.

Определение.

         Решением уравнения

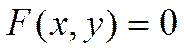
называется упорядоченная пара чисел 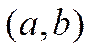 такая, что при подстановке первого элемента пары (числа ) вместо  и второго (числа ) вместо , получаем верное числовое равенство

.

Например,  пара чисел  является решением уравнения

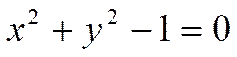
так как

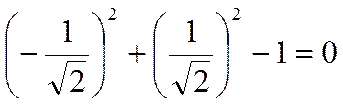
есть верное числовое равенство.

         Далее будем считать, что на плоскости задана Декартова система координат. Введем понятие уравнения кривой на плоскости.

Определение.

        Пусть на плоскости имеется кривая (при этом прямая тоже называется кривой). Уравнение  называется уравнением данной кривой если:

1) координаты любой точки,  лежащей на кривой,  являются решением уравнения , т.е.  есть верное числовое равенство;

2) если пара чисел  есть решение уравнения , т.е.  есть верное числовое равенство, то точка  лежит на кривой.