Доказательство.
Пусть даны векторы ![]() и
и ![]() .
Отложим от общей точки
.
Отложим от общей точки
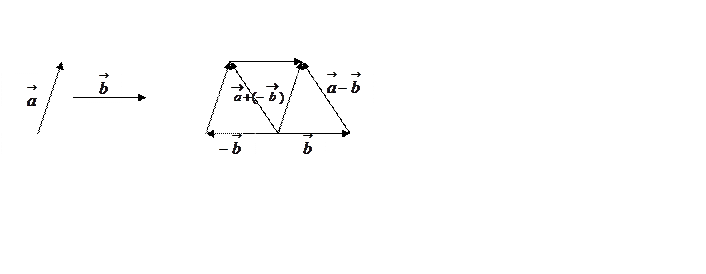
Рис. 9.
![]() векторы
векторы
![]() ,
, ![]() и
и
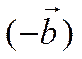 . Векторы
. Векторы ![]() и
и
![]() сложим по правилу параллелограмма.
Фигура
сложим по правилу параллелограмма.
Фигура ![]() является параллелограммом. Поэтому
векторы
является параллелограммом. Поэтому
векторы 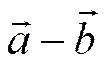 и
и 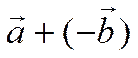 равны.
Отметим, что аналогичное свойство есть у чисел.
равны.
Отметим, что аналогичное свойство есть у чисел.
Введем еще одну операцию с векторами – умножение вектора на число.
Определение.
Пусть дан вектор ![]() и число
и число ![]() .
Произведение числа
.
Произведение числа ![]() на вектор
на вектор ![]() называется вектор, обозначаемый
называется вектор, обозначаемый ![]() и определяемый следующими условиями
(при
и определяемый следующими условиями
(при ![]() ):
):
1) вектор ![]() коллинеарен
вектору
коллинеарен
вектору ![]()
2) 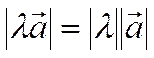
3) вектор 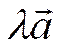 сонаправлен
с вектором
сонаправлен
с вектором ![]() если
если ![]() ипротивонаправлен
вектору
ипротивонаправлен
вектору ![]() , если
, если ![]() .
Если
.
Если ![]() или
или ![]() ,
то по определению полагают, что
,
то по определению полагают, что ![]() . При этом
свойство два остается справедливым.
. При этом
свойство два остается справедливым.
Рассмотрим пример.
Пример.
Дан вектор ![]() и число
и число ![]() .
Построить вектор
.
Построить вектор ![]() .
.

Рис. 10.
Решение.
Возьмем в пространстве
произвольную точку ![]() и через нее проведем
прямую, параллельную вектору
и через нее проведем
прямую, параллельную вектору ![]() . От точки
. От точки ![]() отложим отрезок, длина которого равна
отложим отрезок, длина которого равна
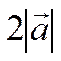 . Стрелку поставим у того конца
отрезка, чтобы получившийся вектор был сонаправлен с вектором
. Стрелку поставим у того конца
отрезка, чтобы получившийся вектор был сонаправлен с вектором ![]() . Построенный вектор и будет равен
вектору
. Построенный вектор и будет равен
вектору ![]() . Действительно, он сонаправлен с
. Действительно, он сонаправлен с ![]() , а дина его равна числу
, а дина его равна числу 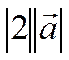 .
.
Перечислим свойства операции умножения числа на вектор.
Теорема 6.
Имеют место следующие свойства операции умножения на число:
1) 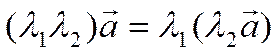
2) ![]()
3) 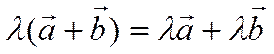
4) 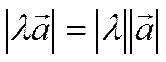
Эти свойства следуют из определения операций сложения и умножения на число и доказываются с помощью элементарной геометрии.
С помощью операции умножения числа на вектор можно сформулировать необходимое и достаточное условие коллинеарности двух векторов.
Теорема 7.
Пусть даны два
ненулевых вектора ![]() и
и ![]() .
Для того, чтобы они были коллинеарны необходимо и достаточно, чтобы существовало
число
.
Для того, чтобы они были коллинеарны необходимо и достаточно, чтобы существовало
число ![]() такое, что справедливо равенство
такое, что справедливо равенство 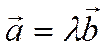 .
.
Доказательство.
Если 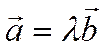 , то согласно определения
произведения числа на вектор векторы
, то согласно определения
произведения числа на вектор векторы ![]() и
и ![]() коллинеарны.
коллинеарны.
Обратно. Пусть ![]() и
и ![]() коллинеарны
и сонаправлены.
коллинеарны
и сонаправлены.
Пусть
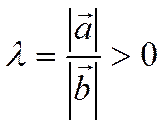 (1)
(1)
Тогда 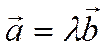 .
В самом деле,
.
В самом деле, ![]() и
и ![]() сонаправлены
(т.к.
сонаправлены
(т.к.![]() ) и имеют одинаковую длину:
) и имеют одинаковую длину: 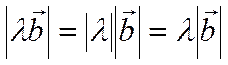 (по определению умножения вектора на
число и т.к.
(по определению умножения вектора на
число и т.к. ![]() ). Длина вектора
). Длина вектора ![]() равна
равна 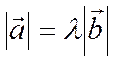 .
Это следует из соотношения (1). Если
.
Это следует из соотношения (1). Если ![]() и
и ![]() противонаправлены, то положим
противонаправлены, то положим
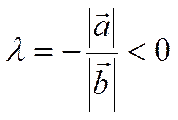 (2)
(2)
Тогда 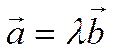 .
В самом деле,
.
В самом деле, ![]() и
и 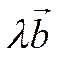 сонаправлены
(т.к.
сонаправлены
(т.к.![]() , а
, а ![]() и
и
![]() противонаправлены). Длины этих
векторов соответственно равны:
противонаправлены). Длины этих
векторов соответственно равны: 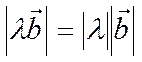 и
и 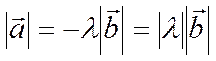 . Последнее равенство следует из
(2) и из-за того, что
. Последнее равенство следует из
(2) и из-за того, что 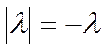 (
(![]() -отрицательное число).
-отрицательное число).
§2. Проекция вектора на ось.
Определение.
Будем говорить, что вектор (ненулевой) коллинеарен прямой, если он параллелен прямой или лежит на этой прямой.
Дадим определение оси.
Определение.
Осью называется пара геометрических объектов – прямая и коллинеарный ей вектор. Такой вектор называется направляющим вектором оси или направляющим вектором прямой.

Рис. 11
Направляющий вектор оси обычно располагают на самой прямой. Так как длина направляющего вектора несущественна, то на прямой указывают только конец направляющего вектора в виде стрелки, а начало направляющего вектора не указывает.
Таким образом, на прямой можно выбрать два противоположных направления. Поэтому иногда говорят, что ось – это прямая с выбранным направлением или направленная прямая.
Если направляющий
вектор оси обозначен, например буквой ![]() ,
то саму ось (то есть пару – вектор плюс прямая) будем обозначать символом «ось
,
то саму ось (то есть пару – вектор плюс прямая) будем обозначать символом «ось ![]() » (см. Рис. 14)
» (см. Рис. 14)
Дадим определение орта оси.
Определение.
Если длина
направляющего вектора оси равна единице, то такой направляющий вектор оси
называется ортом оси. Если ось обозначена как «ось ![]() »,
то орт оси будем обозначать символом
»,
то орт оси будем обозначать символом ![]() .
.
Определение.
Пусть вектор ![]() коллинеарен оси (т.е. либо
параллелен оси, либо лежит на ней). Будем говорить, что вектор
коллинеарен оси (т.е. либо
параллелен оси, либо лежит на ней). Будем говорить, что вектор ![]() сонаправлен с осью, если он
сонаправлен с напраляющим вектором оси и противонаправлен с осью, если он
противонаправлен направляющему вектору оси.
сонаправлен с осью, если он
сонаправлен с напраляющим вектором оси и противонаправлен с осью, если он
противонаправлен направляющему вектору оси.
Определим угол между вектором и осью.
Определение.
Пусть даны ось ![]() и вектор
и вектор ![]() .
Угол между вектором
.
Угол между вектором ![]() и направляющим вектором
оси
и направляющим вектором
оси ![]() называется углом между вектором и
осью.
называется углом между вектором и
осью.

Рис.12.
Заметим, что вектор ![]() всегда можно отложить от точки,
лежащей на оси. Тогда этот вектор и ось образуют геометрический угол (Рис. 16).
Величина угла (мера угла) между вектором и осью может находиться в пределах от
0 до
всегда можно отложить от точки,
лежащей на оси. Тогда этот вектор и ось образуют геометрический угол (Рис. 16).
Величина угла (мера угла) между вектором и осью может находиться в пределах от
0 до ![]() радиан или от 0о до 180о.
радиан или от 0о до 180о.
Введем важное понятие вектор-проекции вектора на ось.
Определение.
Пусть имеется ось и какая-
то точка ![]() . Если точка не лежит на оси, то
проекцией точки
. Если точка не лежит на оси, то
проекцией точки ![]() на ось называется точка
пересечения с осью перпендикуляра, опущенного из точки
на ось называется точка
пересечения с осью перпендикуляра, опущенного из точки ![]()
на эту ось. Если точка ![]() лежит на этой оси, то проекцией точки
лежит на этой оси, то проекцией точки
![]() на ось называется сама эта точка.
на ось называется сама эта точка.
Определение.
Пусть даны вектор 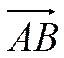 и ось
и ось ![]() .
.
Обозначим через![]() проекцию точки
проекцию точки ![]() на ось
на ось ![]() ,
а через
,
а через ![]() проекцию точки
проекцию точки ![]() на ось
на ось ![]() .
Вектор
.
Вектор 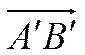 называется вектор-проекцией вектора
называется вектор-проекцией вектора 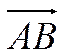 на ось
на ось ![]() (см.
Рис. 17).
(см.
Рис. 17).
Таким образом, вектор ![]() лежит на оси и, следовательно,
коллинеарен оси. Поэтому, если
лежит на оси и, следовательно,
коллинеарен оси. Поэтому, если 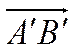 не нулевой вектор,
то он либо сонаправлен с осью, либо противонаправлен с ней. Если вектор
не нулевой вектор,
то он либо сонаправлен с осью, либо противонаправлен с ней. Если вектор ![]() перпендикулярен оси, то его
вектор-проекция является нулевым вектором.
перпендикулярен оси, то его
вектор-проекция является нулевым вектором.

Рис. 13.
Введем важное понятие проекции вектора на ось.
Определение.
Пусть вектор ![]() есть вектор-проекция вектора
есть вектор-проекция вектора ![]() на ось
на ось![]() .
Проекцией вектора
.
Проекцией вектора ![]() на ось
на ось ![]() называется число, модуль которого
равен длине вектора
называется число, модуль которого
равен длине вектора ![]() , а знак выбирается «+»,
если вектор
, а знак выбирается «+»,
если вектор ![]() и ось сонаправлены и выбирается знак
«-», если вектор
и ось сонаправлены и выбирается знак
«-», если вектор ![]() и ось противонаправлены.
Проекция вектора
и ось противонаправлены.
Проекция вектора ![]() на ось
на ось ![]() обозначается символом
обозначается символом 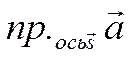 . Таким образом,
. Таким образом, 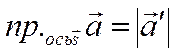 , если вектор
, если вектор ![]() и
ось
и
ось ![]() сонаправлены и
сонаправлены и 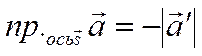 , если вектор
, если вектор ![]() и
ось
и
ось ![]() противонаправлены.
противонаправлены.
Если ![]() , то полагаем по определению, что
, то полагаем по определению, что ![]() .
.
Определим также проекцию вектора на вектор.
Определение.
Пусть даны векторы ![]() и
и ![]() ,
причем
,
причем ![]() ненулевой вектор. Если через вектор
ненулевой вектор. Если через вектор ![]() провести прямую, то получим ось с
направляющим вектором
провести прямую, то получим ось с
направляющим вектором ![]() . Проекция вектора
. Проекция вектора ![]() на эту ось называется проекцией
вектора
на эту ось называется проекцией
вектора ![]() на вектор
на вектор ![]() и
обозначается
и
обозначается 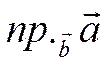 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.