Оптика фотонных кристаллов: Методические указания к практическим занятиям, страница 9

	Математический маятник	Груз на пружине	Электрический контур
Уравнение
Циклическая частота
Инерция
Жесткость

В них одинаково описываются вынужденные и затухающие колебания, биения в связанных колебательных системах.

С другой стороны, одномерный фотонный кристалл представляет систему плоскопараллельных пластинок, каждая из которых представляет собой колебательный контур (резонатор Фабри-Перо) для световой волны, подобно тому, как струна – резонатор для поперечной упругой волны, а пустота внутри гитары – резонатор для продольной звуковой волны.

Вне стен физической лаборатории практически невозможно получить и исследовать фотонный кристалл. Напрашивается аналогия его с легко осуществимой цепочкой электрических колебательных контуров, которая образует фильтр в мегагерцовом диапазоне. Однако, оказывается очень трудно построить такой фильтр с несколькими запрещенными и разрешенными полосами.

Объясните принципиальное отличие колебаний в оптической пластинке от колебаний в электрическом контуре.

Раздел 7. Распростарнение интенсивного лазерного излучения
 в фотонно-кристаллических средах

Задача 3.7.1

С какими особыми точками в спектре собственных частот двумерного фотонного кристалла (см. лекцию 15, рис. 15.1) связаны особенности в плотности фотонных состояний.

Задача 3.7.2

Получить зависимость нормированной плотности фотонных состояний  (см. лекцию 15) одномерного фотонного кристалла от длины волны в интервале 300 – 700 нм:

а) Образец с числом слоев , с толщиной слоев  мкм,  мкм, с показателями преломления , ;

б) Число слоев в образце , остальные параметры те же, что и для случая а).

в) Структура фотонного кристалла отличается от случая а) лишь появлением в центре кристалла дефектного слоя с  мкм. Сравнить плотности фотонных состояний, соответствующие дефектной моде и краям фотонной запрещенной зоны.

Задача 3.7.3

Чем обусловлена способность фотонных кристаллов изменять интенсивность излучения зондовых атомов, внедренных в периодическую решетку, в зависимости от частоты внедренного в кристалл диполя и положения его в решетке?

Задача 3.7.4

Получить зависимость плотности фотонных состояний ФК от длины волны. Параметры структуры ФК отличаются от соответствующих параметров задачи 3.7.2 лишь изменением  на значение .

Задача 3.7.5

Показать, что в случае центросимметричных кристаллов нелинейность сред определяется в первом порядке кубической восприимчивостю (кубично-нелинейные среды).

Задача 3.7.6

Показать, что при учете кубической нелинейности волновое уравнение в одномерном фотонном кристалле может быть представлено в виде формулы (16.8) лекции 16.

Задача 3.7.7

Установить в какую сторону смещается запрещенная зона и дефектная мода в задаче 3.6.14 с увеличением интенсивности излучения, если при этом коэффициент преломления алмаза увеличится на 1%

Задача 3.7.8

Получить выражение для трансфер-матрицы (16.13) (лекция 16) модеифицированной для описания влияния керровской нелинейности на прохождение лазерного излучения в одноменых фотонных кристаллах.

Раздел 8. Фотонный холестерический жидкий кристалл

Задача 3.8.1

Тензор диэлектрической проницаемости  холестерического жидкого кристалла (или холестерика) определяется формулой

                                  .

где ,  – диэлектрические проницаемости для электрического поля соответственно параллельного и нормального единичному вектору (, называемому директором), который задает ориентацию молекул изменяющуюся с изменением  по спирали:

                                     , , .

Пространственный период спирали директора .

Определить связь между частотой и волновым вектором электромагнитной волны распространяющейся вдоль оси спирали холестерика.

Задача 3.8.2

В реальных холестерических жидких кристаллах различие между  и  относительно мало

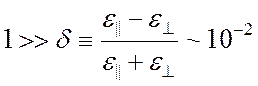                                              .                  (1)

В этом случае формулу (17) (см. пример решения задачи 3.8.1) можно упростить

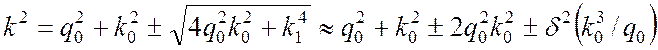            ,                                                                (2)

Распространению волны в положительном направлении оси  соответствуют положительные значения корней этого уравнения. При  это корни

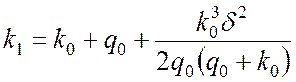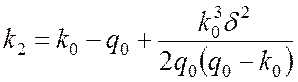                 , .                                                               (3)

Покажите, что в пределе  имеются два решения, которые соответствуют право- и лево-циркулярной поляризованным волнам, так как в этом случае  или . При конечных  эти волны эллиптически поляризованы.

Задача 3.8.3. Спектр отражения холестерика с дефектами

Толщина пленки холестерического жидкого кристалла составляет 25  ( – шаг спирали). Параметры идеальной структуры пленки такие же, как в лекции 17: , ,  нм. Дефектом структуры жидкого кристалла является локально измененный шаг спирали. Используя полученную в лекции формулу (17.8) для коэффициента отражения при нормальном падении света на образец исследовать в области 400 – 600 нм

а) зависимость коэффициента отражения от длины волны  для идеального кристалла;

б) зависимость коэффициента отражения света от холестерика от  в случае если шаг спирали в центре пленки увеличен по сравнению с шагом идеальной структуры и равен 1,2 ;

в) зависимотсь коэффициента отражения от  для холестерика с двумя одинаковыми дефектами структуры. Рассмотреть случаи, когда расстояние между дефектами, симметрично расположенными относительно центра пленки равно 13  или 15 .

г) Провести анализ полученных результатов в сравнении с результатами лекции 17 и решенной задачи 3.6.16.

При расчетах воспользоваться программой, приведенной при решении задачи 3.6.16 о спектре пропускания слоистой среды с дефектами структуры, адаптировав ее для своих целей.

5. Примеры решения задач

Задача 1.1.8

Если в разложении (2.32) частоты в окрестности  можно пренебречь членами второго и высшего порядков, то огибающая лазерного импульса сохраняет свою форму. Рассмотрите случай, когда член второго порядка не является малым и его необходимо учитывать, в то время как членами высшего порядка можно пренебречь:

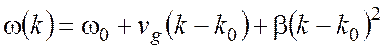                                     ,         (1)