![]() (6.5)
(6.5)
т.к. в
фильтрах Z1 и Z2являются реактивными сопротивлениями, противоположного характера, то параметр
А11 является действительным числом. В этом случае ![]() должно быть
равно нулю, а т.к в
полосе пропускания фильтра затухание
должно быть
равно нулю, а т.к в
полосе пропускания фильтра затухание ![]() равно
равно ![]() , тогда
, тогда
![]()
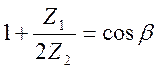
Поскольку меняется в пределах от -1 до 1, то
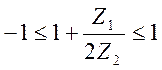
Или
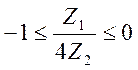
что и требовалось доказать.
6.4. ФИЛЬТРЫ HИЖНИX ЧАСТОТ, ИХ ПАРАМЕТРЫ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
В фильтрах нижних частот последовательные плечи содержат индуктивность, а параллельные - емкость /рис.6.4/
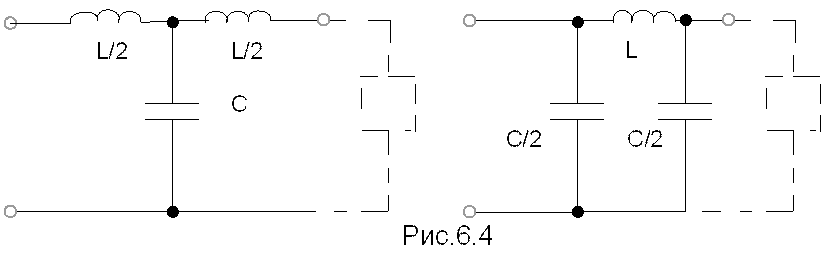
В таких фильтрах колебания низких частот встретят со стороны индуктивности небольшое сопротивление и пройдут через нее к сопротивлении нагрузки, ответвляясь в емкость лишь в очень малой степени, т.к. емкость на низких частотах представляет большое сопротивление. Колебания высоких частот задерживаются индуктивностью и ответвляются в ветви с емкостями, поэтому на нагрузку будет проходить лишь небольшая часть входного напряжения.
Для определения граничных частот полосы пропускания воспользуемся равенствами из выражения /6.3/. Т.к.
![]()
![]() ,
а
,
а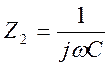 ,
,
то
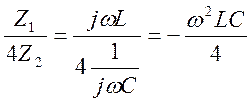 /6.6/
/6.6/
Приравнивая полученное выражение сначала нулю, а затем единице, получим
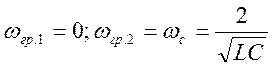 /6.7/
/6.7/
Таким образом, полоса протекания ФНЧ простирается
от w=О до ![]() область частот
область частот ![]() является полосой затухания.
является полосой затухания.
Характеристические сопротивления для Т и П-образной схем фильтров, будут равны:
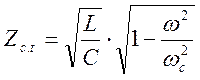 (6.8)
(6.8)
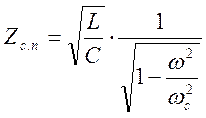 (6.9)
(6.9)
Из выражений (6.8) и (6.9) видно, что характеристическое сопротивление изменяется с изменением частоты. что значит, что подключая в качестве нагрузки активное сопротивление можно добиться согласованного режима работы лишь в области частот от нуля до некоторой частоты, меньшей частоты среза.
График зависимостей ![]() и
и ![]() приведен
на рис.6.5
приведен
на рис.6.5
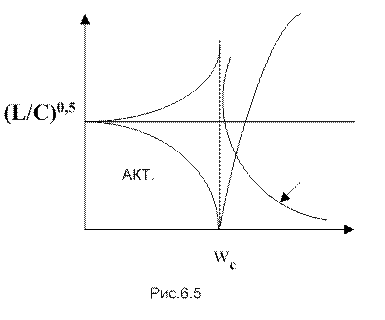
Можно показать, что частотные зависимости и изменяются следующим образом:
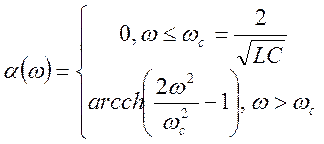 (6.10)
(6.10)
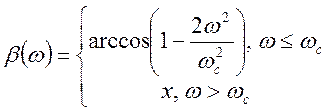 (6.11)
(6.11)
Графики
частотных зависимостей ![]() и
и ![]() приведены
на рис.6.6.
приведены
на рис.6.6.
 Расчет фильтра заключается в определении
значений L и С по заданным частоте среза wc и сопротивлению нагрузки, на которую
будет работать фильтр.
Расчет фильтра заключается в определении
значений L и С по заданным частоте среза wc и сопротивлению нагрузки, на которую
будет работать фильтр.
Приближенно полагая, что
в полосе пропускания характеристическое сопротивление равно 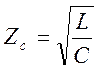 и
и 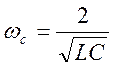 используя
равенство получаем
используя
равенство получаем
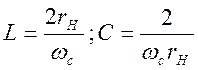 (6.12)
(6.12)
ПРИМЕР. Определить значения L и С фильтра нижних частот, полоса пропускания которого лежит .от 0 до 10 кГц, а сопротивление нагрузки
![]() =10
кОм.
=10
кОм.
Значения L и С при заданных условиях будут
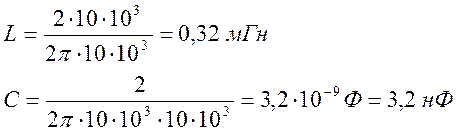
6.5. ФИЛЬТРЫ ВЕРХНИХ ЧАСТОТ, ИХ ПАРАМЕТРЫ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
В фильтрах верхних частот /ФВЧ/ последовательные плечи Т-образной и П-образной схем содержат емкость С, а параллельные -индуктивность L (рис.6.7).
 Токи высокой
частоты встретят со стороны емкостей небольшое сопротивление и пройдут через них
к нагрузке, ответвляясь в индуктивности в очень малой степени, т.к. индуктивности
представляют большое сопротивление колебаниям высоких частот.
Токи высокой
частоты встретят со стороны емкостей небольшое сопротивление и пройдут через них
к нагрузке, ответвляясь в индуктивности в очень малой степени, т.к. индуктивности
представляют большое сопротивление колебаниям высоких частот.
Токи низких частот сильно ослабляются емкостями, поскольку они представляют для них большое сопротивление и ответвляются через индуктивность, которая на низких частотах представляет малое сопротивление, поэтому через нагрузку будет протекать лишь незначительная часть входного тока.
Для определения граничных частот полосы пропускания воспользуемся равенством: из выражения.
Так
как 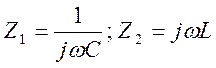 ,
,
то.
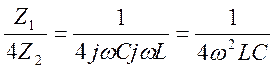 (6.13)
(6.13)
Приравнивая 6.13 сначала единице, а затем нулю, получаем
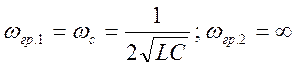 (6.14)
(6.14)
Таким образом, полоса пропускания ФВЧ простирается от 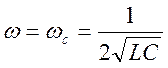 до
до ![]()
Область
частот ![]() является полосой затухания.
является полосой затухания.
Характеристические сопротивления для Т- и П-образной схемы фильтров будут равны
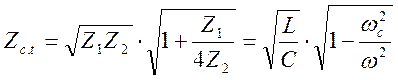 (6.15)
(6.15)
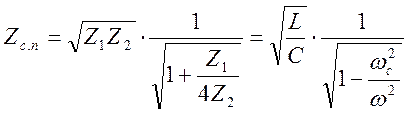 (6.
16)
(6.
16)
Из
приведенных выражений видно, что характеристические сопротивления
фильтров изменяются с изменением частоты, это значит, что подключая в
качестве нагрузки активное сопротивление 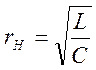 можно добиться
согласованного режима работы лишъ в области частот - от некоторой
частоты
можно добиться
согласованного режима работы лишъ в области частот - от некоторой
частоты ![]() большей, чем частота среза, до очень
больших
частот
большей, чем частота среза, до очень
больших
частот![]() .
.
 Графики
зависимости приведены На. рис.6.8 можно также показать, что зависимости
Графики
зависимости приведены На. рис.6.8 можно также показать, что зависимости![]() меняются следующим образом:
меняются следующим образом:
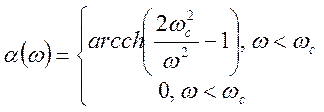 (6.16)
(6.16)
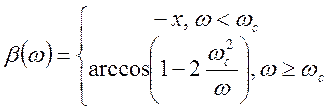 (6.17)
(6.17)
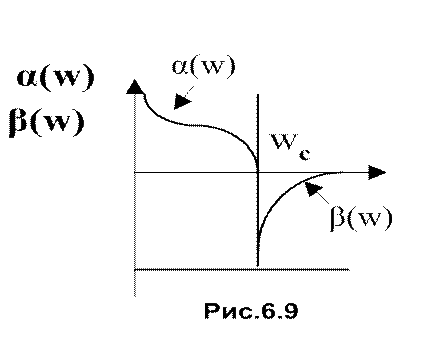
Графики частотных зависимостей приведены на рис.6.9
1. Приближенно
можно считать, что ФВЧ пропускает от источника в нагрузку, работая в согласованном
режиме колебания токов высоких частот, если ![]() .
.
2. Приближенно можно считать, что согласованный режим
работы обеспечивается, если 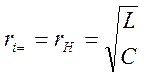
Расчет Фильтра
Расчет
фильтра заключается в определении значение L и С, по заданным частоте
среза и сопротивлению нагрузки. Приближенно полагая, что в полосе
пропускания характеристическое сопротивление равно 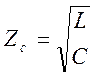 и
используя
и
используя 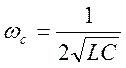 получаем:
получаем:
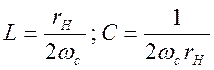 (6.18)
(6.18)
ПРИМЕР 6.1. Определить значения L и С фильтра верхних частот, полоса пропускания которого лежит в пределах от10 кГц до бесконечности, а сопротивление нагрузки r н = 10 кОм.
РЕШЕНИЕ.
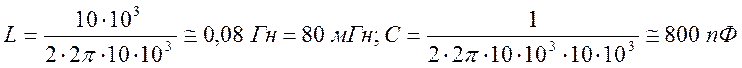
значения L и С при заданных условиях будут равны.
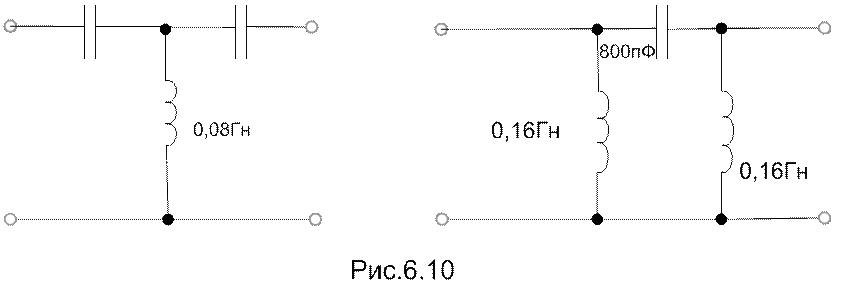
При этом элементы Т и П-образной схем будут иметь следующие значения (приведены на рис.6.10)
 6.6.
ПОЛОСОВЫЕ ФИЛЬТРЫ, ИХ ПАРАМЕТРЫ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
6.6.
ПОЛОСОВЫЕ ФИЛЬТРЫ, ИХ ПАРАМЕТРЫ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
В полосовых фильтрах (ПФ) последовательные плечи Т-образной и П-образной схем содержат последовательные контуры, а параллельные плечи - параллельные контуры (рис.6.11).
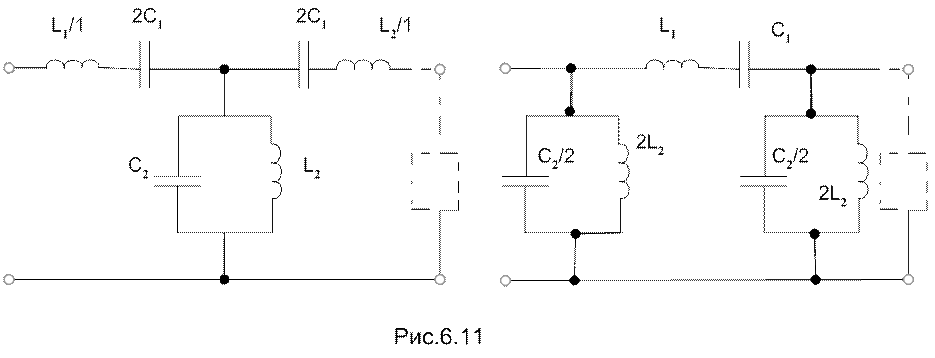
Известны частотные зависимости сопротивлении последовательного и параллельного контуров от частоты, которые приведены на pис.6.12
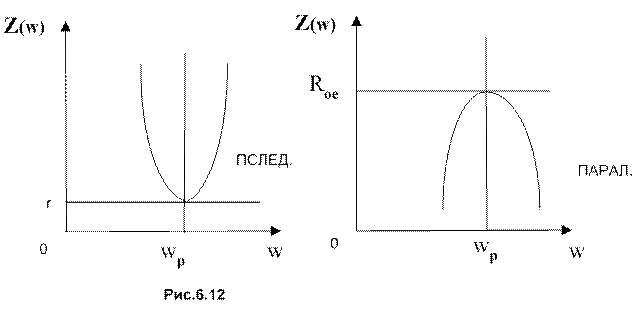
Как видно из рис.6.12, сопротивление последовательного контура на резонансной частоте минимально, а сопротивление параллельного контура максимально.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.