Переходной процесс связан с энергоемкими элементами, входящими в цепь. К энергоемким элементам относят емкость и индуктивность. Исходя из того, что запасенная энергия является непрерывной функцией времени, то следует, что ток через индуктивность и напряжение на емкости, также являются непрерывными функциями времени. Этот вывод формулируется в виде законов коммутации.
Первый закон коммутации: В начальный момент времени после коммутации ток через индуктивность сохраняет такое же значение, как и непосредственно перед коммутацией: iL(+0) = iL(-0).
Второй закон коммутации: В начальный момент времени после коммутации напряжение на емкости сохраняет такое же значение, как и непосредственно перед коммутацией: uC(+0) = uC(-0).
6.4. Методы анализа линейных цепей при импульсном воздействии
Задача анализа цепи заключается к отысканию отклика при известном входном сигнале (воздействии).
При импульсном воздействии x(t) – произвольная функция времени.
При произвольном входном сигнале основными методами анализа цепей являются:
1) классический метод;
2) спектральный метод;
3) операторный метод;
4) временной (метод интеграла Дюамеля).
Он сводится к составлению и решению дифференциального уравнения, устанавливающего связь между откликом и воздействием. Порядок применения метода следующий.
1) составление дифференциального уравнения и приведение его к стандартному виду.
Уравнение составляется на основе законов Ома и Кирхгофа, а также с использованием метода контурных токов, узловых потенциалов и других. При составлении уравнения используют следующие соотношения:
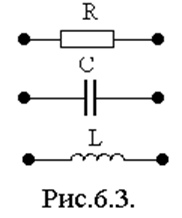
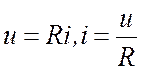
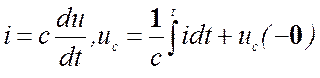
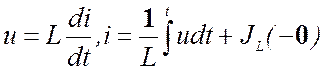
При составлении уравнения за неизвестные принимают переменные состояния цепи, т.е. величины, которые отражают энергетическое состояние цепи. К ним относят uc, и iL. Составленные уравнения цепи после преобразований, приведения подобных членов и дифференцирования сводят к неоднородному линейному уравнению.
 |
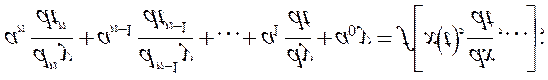где: y(t) – отклик; х(t) – воздействие; ai – постоянные, зависящие от R, L, C
n – порядок дифференциального уравнения. Порядок ДУ зависит от числа реактивных элементов и схемы их соединения. В простейшем случае число реактивных элементов равно n.
2) Запись общего решения ЛНДУ.
Оно состоит из суммы двух составляющих:
y(t) =y1(t) + y2(t).
y1(t) – это общее решение однородного линейного дифференциального уравнения, когда f=0. Это решение не зависит от воздействия (x) и называется свободной составляющей общего решения. Это решение известно и равно
,
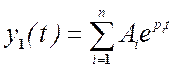где pi – корни характеристического уравнения, Ai- постоянные интегрирования.
y2(t) – это частное решение НЛДУ, оно зависит от x(t), а потому называется вынужденной составляющей общего решения.
3) Нахождение вынужденной составляющей y2(t).
Она зависит от воздействия. Если входной сигнал имеет
стационарный режим, то за частное решение принимают решение уравнения в
установившемся (стационарном) режиме. При ступенчатом воздействии такой режим
имеет место, когда t ® ¥. Это соответствует постоянной составляющей, т.е. гармоническому
сигналу с нулевой частотой, 
,
а потому y2(t)
находят из схемы замещения исходной цепи при w=0.
4) Нахождение pi.
Коэффициенты экспоненты находятся как корни
характеристического уравнения, которое получают из дифференциального путем
замены производных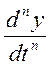 
на 
:
.
5) Нахождение постоянных интегрирования Ai.
Постоянные интегрирования общего решения определяются из начальных условий (при t = 0) для искомой функции и ее производных.
; 
; 
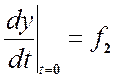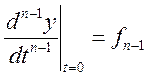
Конкретные значения этих функции при t=0 находят из схем замещения исходной цепи при t =+0 с учетом законов коммутации для L, C элементов. Если входной сигнал ступенчатая функция, то мгновенному изменению входного сигнала при t = 0 соответствует гармонический сигнал с w ® ¥, а потому искомые значения находят из схемы замещения исходной цепи при w ® ¥.
6) Анализ корней характеристического уравнения и запись окончательного решения.
6.4.2. Спектральный метод анализа
Спектральный метод применяется в
тех случаях, когда входной сигнал может быть представлен спектром. Сигнал имеет
спектр, когда он обладает конечной энергией, т.е. удовлетворяет условию:
.
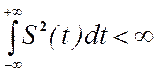Этапы применения метода:
1) по известному сигналу находится его спектр
-
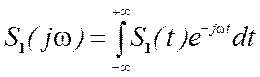прямое преобразование Фурье.
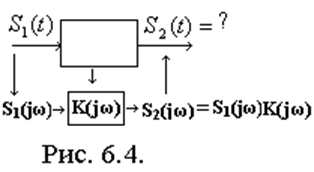
2) По известной схеме электрической цепи определяется частотная передаточная характеристика:
.
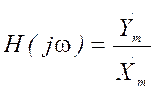3) находится спектральная плотность выходного сигнала
.
4) по известному спектру выходного сигнала находится сам выходной сигнал
.
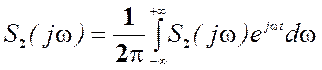6.4.3. Операторный метод анализа
Применим при любых входных сигналах. Метод основан на том, что функции f(t) вещественной переменной t, которую называют оригиналом, ставится в соответствие функция F(p) комплексной переменной p=s+jω, которую называют изображением. В результате этого производные и интегралы от оригиналов заменяются алгебраическими функциями от соответствующих изображений (дифференцирование заменяется умножением на оператор р, а интегрирование – делением на него), что в свою очередь определяет переход от системы интегро-дифференциальных уравнений к системе алгебраических уравнений относительно изображений искомых переменных. При решении этих уравнений находятся изображения и далее путем обратного перехода – оригиналы.
Порядок расчета переходных характеристик заключается в следующем:
1) находим операторное представление входного сигнала
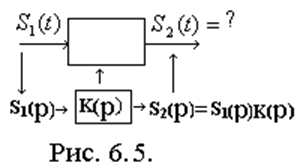
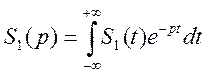- прямое преобразование Лапласа.
2) по известно схеме цепи находим операторную передаточную функцию цепи
3) находим операторное представление отклика
.
4) с помощью обратного преобразования Лапласа находим отклик цепи
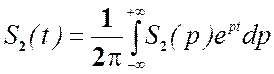
Важнейшим моментом при этом в практическом плане является необходимость определения только независимых начальных условий, что существенно облегчает расчет переходных процессов в цепях высокого порядка по сравнению с классическим методом.
Изображение 
заданной функции 
определяется в соответствии
с прямым преобразованием Лапласа:
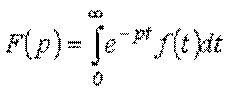
В сокращенной записи соответствие между изображением и оригиналом обозначается, как:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.