Система. Элементы системы. Математические модели динамических систем. Входные воздействия. Математическое описание объектов или систем с помощью графов. Математическое описание многомерных объектов или систем, страница 6

1.  Изучить понятие многомерных непрерывных и импульсных систем.

2.  Изучить построение математической модели многомерных систем.

Непрерывная система, состоящая из непрерывных элементов и, имеющая несколько входных и выходных каналов, называется непрерывной многомерной системой.

 

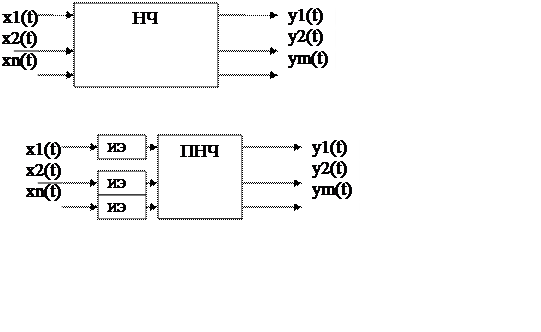
Система, содержащая приведенную непрерывную части, несколько импульсных элементов, несколько входных и выходных каналов называется многомерной импульсной системой.

Импульсные элементы могут вырабатывать импульсы различной амплитуды, длительности, частоты. В том случае, если периоды повторения во всех импульсных элементах совпадают, то многомерная импульсная система называется синхронной. Если в синхронной импульсной системе совпадают моменты возникновения импульсов, то систему называют синфазной.

При математическом описании многомерной непрерывной системы, получают систему дифференциальных уравнений, связывающих между собой входную и выходную величины. Количество уравнений будет определяться количеством выходных сигналов.

Обозначим:

    -  вектор столбец входных переменных,

   -  вектор столбец выходных переменных,

   -  вектор столбец внутреннего состояния системы.

Тогда, с помощью уравнений состояния многомерную непрерывную систему можно описать в виде:

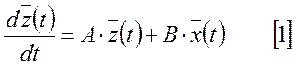
При этом выходной сигнал будет определяться уравнением:

.

Размеры матриц:

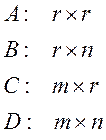
В том случае, если у системы 1 вход и 1 выход, получаем:

.

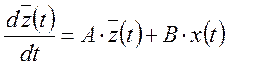
Размеры матриц:

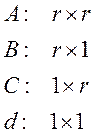
Любую многомерную непрерывную систему можно записать с помощью функциональной зависимости:

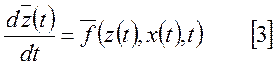
При математическом описании дискретных многомерных систем, состояние системы будет определяться:

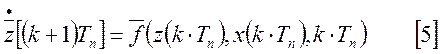
Если период квантования постоянен и равен 1, то получим.

Передаточная функция многомерной системы.

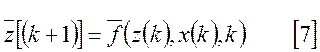
При определении передаточных функций многомерной системы определяется передаточная функция для каждого выхода системы по каждому входу:

.

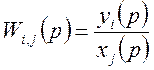Тогда передаточной функцией многомерной системы будет являться матрица с элементами .

Каждый выходной сигнал системы будет определяться так:

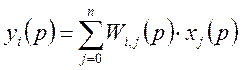
Количество передаточных функций многомерной системы равно произведению .

Определим матричное выражение для передаточной матрицы. Для этого используем уравнения состояния и выхода в векторной форме.

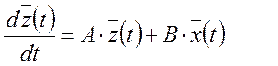
Преобразуем по Лапласу.

выразим z(p) из [9].

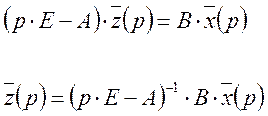
Подставим в [10].

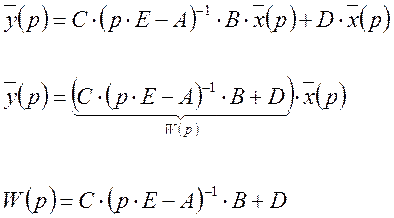
Последнее выражение и является передаточной матрицей системы.

Если p=jw – чисто мнимое число, то получаем частотную форму передаточной матрицы W(jw).

Выражение  является матричной импульсной переходной функцией. Каждый элемент этой матрицы (i,j) является откликом выходной i-той величины на изменение j-той входной величины, обусловленное δ функцией.

Матрица , определяемая как:

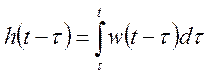
называется переходной матрицей многомерной системы. Каждый элемент этой матрицы (i,j) определяет реакцию i-той выходной величины на изменение j-той входной величины на 1(t).

Вопросы для самоконтроля.

1.  Непрерывная многомерная система. Способы задания.

2.  Импульсная многомерная система. Способы задания.

3.  Передаточная функция многомерных систем.

ЛЕКЦИЯ 7.

АНАЛИЗ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ.

Цель. Провести анализ систем автоматического управления.

Задачи:

1.  Анализ устойчивости систем управления.

2.  Анализ качества систем управления.

Анализ устойчивости.

Система называется устойчивой, если при подаче на ее вход любого возмущающего воздействия, она через некоторый промежуток времени возвращается в устойчивое состояние.

При исследовании устойчивости системы используют  различные алгебраические, частотные и так далее методы и критерии. Рассмотрим определение устойчивости системы по ее дифференциальному уравнению.

Пусть система описывается дифференциальным уравнением вида:

.

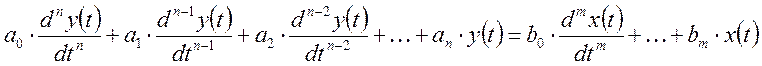Решение может быть представлено в виде суммы:

Для оценки устойчивости рассмотрим составляющую . Она получается при решении характеристического уравнения:

Определяя корни, получившегося характеристического уравнения для составляющей  можно получить:

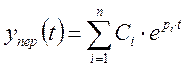
В общем случае корни p_i –  мнимые числа:

Рассмотрим два комплексно-сопряженных корня:

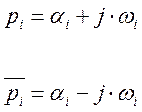
И рассмотрим их сумму:

Преобразовав полученную сумму, можно определить, что сумме соответствующих 2 комплексно-сопряженных корням соответствует:

Получим, что паре корней соответствует синусоида, изменяющаяся по экспоненте. Если , то синусоида будет затухать; если , то синусоида расходится; и если , то будут незатухающие колебания. Следовательно, чтобы система была устойчивой необходимо и достаточно, чтобы все корни характеристического уравнения находились в левой полуплоскости комплексной плоскости. Если хотя бы один из корней находится на мнимой оси, то система находится на гране устойчивости, а если хотя бы один из корней находится в правой полуплоскости – система неустойчива.

Анализ качества.

Анализ качества системы можно проводить с помощью прямых и косвенных оценок качества. При использовании прямых оценок качества, используют непосредственно переходную функцию системы.

При исследовании качества многомерных систем, исследуются качества для каждого входа по каждому выходу при каждом из воздействий. При этом, оставшиеся воздействия считают нулевыми.

Рассмотрим некоторый переходный процесс, имеющий вид.

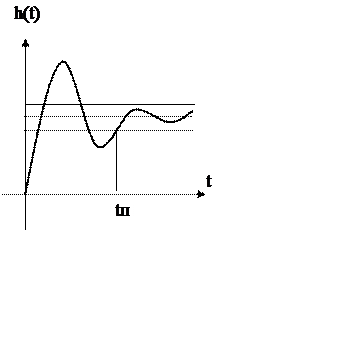
1) время переходного процесса – это величина, характеризующая быстродействие системы и определяется как интервал времени от момента приложения воздействия до момента, когда отклонение регулируемой величины не будет отличаться от установившегося не более чем на 5%.

2) перерегулирование или максимальная динамическая ошибка определяет максимальное отклонение регулируемой величины от установившего значения, выраженное в процентах.

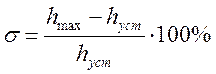
Для реальных систем величина перерегулирования должна быть в пределах 10-30%. В некоторых системах требуется, чтобы величина перерегулирования была близка к 0, а некоторых случаях никаких особых требований не предъявляется.