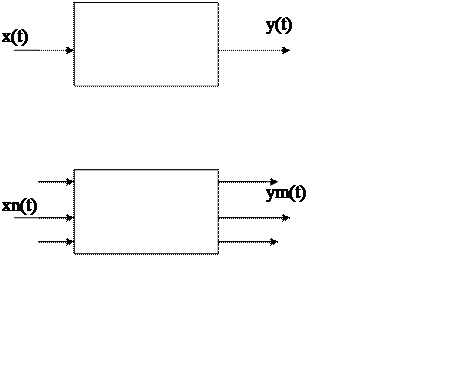
7. Одномерные и многомерные.
Одномерные системы – это системы с одним входом и одним выходом.
Многомерные системы – это системы, которые могут иметь много входов и много выходов.
Вопросы для самоконтроля.
1 Охарактеризуйте способы математического описании систем управления.
2 Назовите типы воздействий на систему, чем они характеризуются.
3 По каким признакам можно классифицировать системы автоматического управления.
4 Чем статические системы отличаются от динамических систем.
5 В чем особенности детерминированных и стохастических систем.
6 Назовите отличительные признаки дискретных и непрерывных систем
Цель. Изучение математических моделей динамических систем.
Задачи:
1. Изучить математические модели линейных динамических систем
2. Изучить математические модели нелинейных динамических систем.
3. Изучить понятие и формы записи передаточной функции.
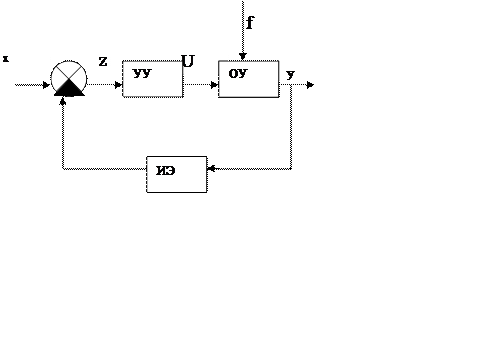
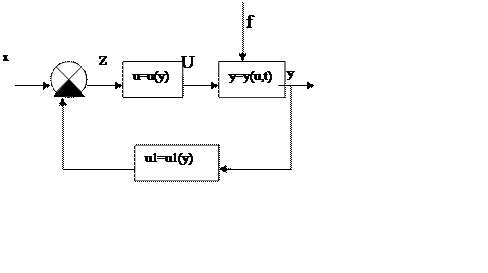
По функциональной схеме составляется структурная схема, представляющая собой набор блоков, внутри которых записывается функциональная зависимость между входом и выходом этого элемента.
Определение.
Уравнения, описывающие изменяющееся во времени состояния системы, называются уравнениями динамики.
При математическом описании и исследовании систем используются линейные уравнения. Для описания нелинейных систем используются нелинейные уравнения. При исследовании таких систем исходные нелинейные уравнения заменяются приближенными линейными.
Рассмотрим метод малых отклонений.
Пусть некоторый элемент описывается нелинейным дифференциальным уравнением вида:
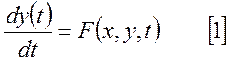
Обозначим невозмущенное состояние через ![]() , а малые отклонения через
, а малые отклонения через ![]() , тогда входной сигнал нашей системы
будет иметь вид:
, тогда входной сигнал нашей системы
будет иметь вид: ![]() , а выходной -
, а выходной - ![]() .
.
Рассмотрим левую часть уравнения:
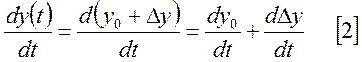
Правая часть уравнения [1] – нелинейная функция.
Разложим ее в ряд Тейлора в окрестности точки ![]() ,
являющейся точкой установившегося состояния. В результате получим:
,
являющейся точкой установившегося состояния. В результате получим:
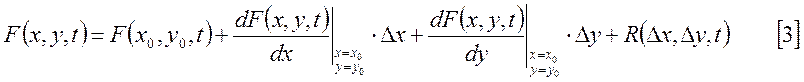
В случае малых отклонений остаточным членом ![]() можно пренебречь. Подставим [2] и [3] в [1].
можно пренебречь. Подставим [2] и [3] в [1].
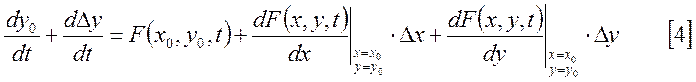
Обозначим:
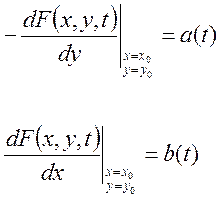
Тогда [4] примет вид:
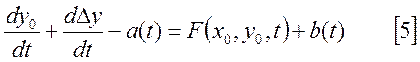
В том случае, когда отклонения ![]() равны
0, то есть система находится в невозмущенном состоянии [5] примет вид:
равны
0, то есть система находится в невозмущенном состоянии [5] примет вид:
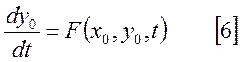
Вычитая [6] из [5] получим уравнения в приращениях, являющиеся линейными:
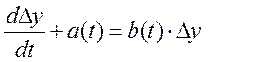 .
.
В общем, виде линейную динамическую систему можно описать с помощью дифференциального уравнения, определяющего связь между входной величиной x(t) и выходной y(t). Это уравнение будет иметь вид:
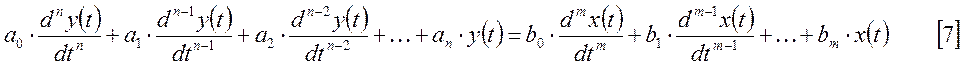
![]() - постоянные
величины, характеризующие параметры звена. Коэффициенты
- постоянные
величины, характеризующие параметры звена. Коэффициенты ![]() -
константы, определяющие параметры входного сигнала.
-
константы, определяющие параметры входного сигнала.
Задавая различные выражения для входного сигнала по уравнению [7], можно определить выходной сигнал y(t), при этом должно быть задано n начальных условий.
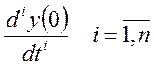
Запишем уравнение установившегося состояния или статическую характеристику элемента. Определить все свойства исследуемого элемента и его переходный процесс можно, решив дифференциальное уравнение [7].
Методы решения.
1. Аналитический – в этом случае решение дифференциального уравнения ищется в общем виде.
2. Численный – в этом случае в общем виде решение не получают, а получают численное значение для заданных входных параметров.
3. Качественный – в этом случае решения уравнения не получают, а определяют некоторые требуемые его свойства.
При аналитическом методе решения уравнения, решение получают в виде:
![]() ,
,
где ![]() - представляет собой решение
однородного дифференциального уравнения [8].
- представляет собой решение
однородного дифференциального уравнения [8].
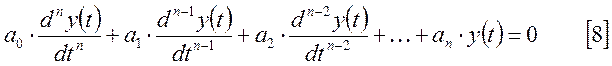
![]() - частное решение неоднородного
уравнения [7].
- частное решение неоднородного
уравнения [7].
Общее решение однородного дифференциального уравнения [8] можно представить в виде:
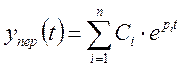
где ![]() - некоторые коэффициенты,
определяемые из начальных условий, а pi – корни характеристического уравнения [9].
- некоторые коэффициенты,
определяемые из начальных условий, а pi – корни характеристического уравнения [9].
![]()
Частное решение уравнения [7] будет зависеть от свойств и вида входного сигнала.
Определить корни характеристического уравнения порядка выше 3 практически невозможно, поэтому для получения аналитических зависимостей выходного сигнала от входного используют операторные методы, основанные на преобразовании Лапласа. В этом случае используется понятие передаточной функции элемента или системы.
Рассмотрим некоторый элемент или систему, на вход которой подали сигнал «x», а на выходе получили «y».

Передаточной функцией системы или элемента называют отношение выходной величины к входной при нулевых начальных условиях.
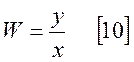
Передаточная функция может быть записана в 4 формах:
1. операторная.
2. стандартная.
3. в форме изображений по Лапласу.
4. частотная.
Введем
в уравнение [7] оператор дифференцирования «р» 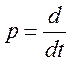 ,
тогда [7] примет вид:
,
тогда [7] примет вид:
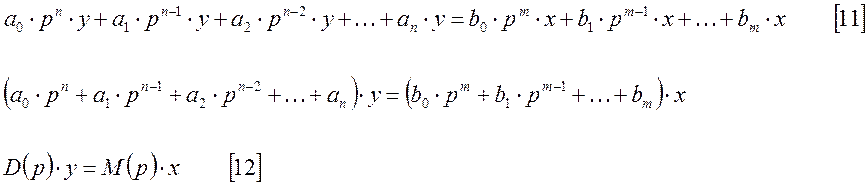
D(p) – характеристический многочлен, а ![]() - характеристическое уравнение.
- характеристическое уравнение.
Используя [12], определим передаточную функцию элемента:
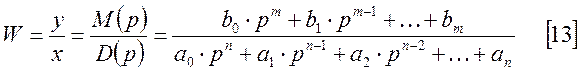
Полученное выражение для передаточной функции называется операторной формой записи передаточной функции.
Преобразуем [13] к виду:
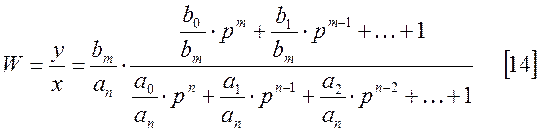
это стандартная форма записи передаточной функции.
Величина 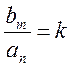 называется
коэффициентом передачи системы,
называется
коэффициентом передачи системы,
Величины
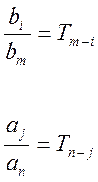
- постоянные времени. Тогда [14] примет вид:
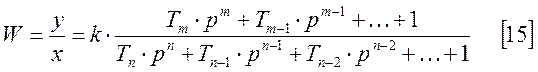
Для получения передаточной функции в форме изображений по Лапласу используют преобразования, приводящие функцию действительного аргумента t в функцию мнимого переменного р.
![]() - преобразование
Лапласа
- преобразование
Лапласа
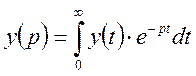
Рассмотрим уравнение [7]. Преобразуем функцию y(t) по Лапласу.
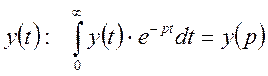
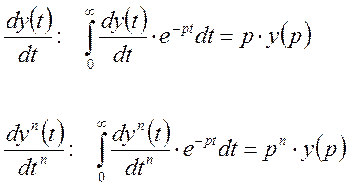
Для правой части [7] можно получить, что:
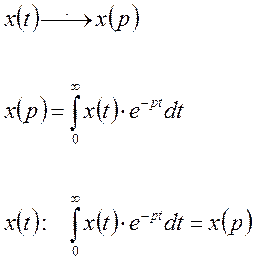
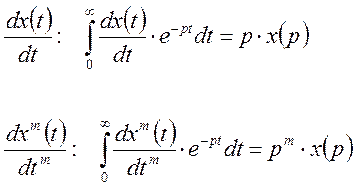
Подставляя в [7], получим:
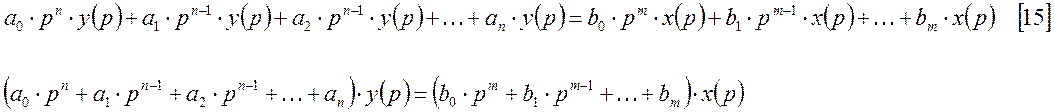
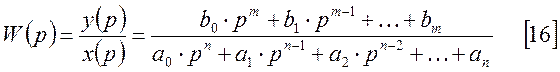
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.