Путь называется элементарным, если ни одна из его вершин не встречается дважды.
Контур – это путь начало и конец, которого совпадают.
Элементарный контур – это контур, у которого все вершины различны.
Петля – это дуга, соединяющая одну и ту же вершину.
Неориентированные графы.
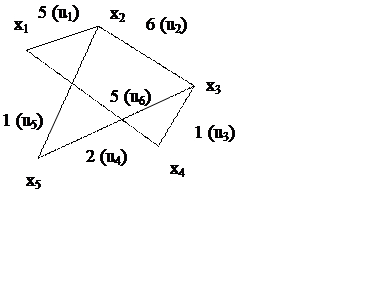
Ребро – это отрезок, соединяющий 2 вершины.
Цепь – это последовательность ребер.
Цикл – это цепь, у которой начало и конец совпадают.
Для обоих графов.
Степень вершины – это число ребер или дуг, входящих или выходящих из вершины.
Граф называется связанным, если любые его две вершины можно соединить путем или цепью.
Дерево графа – это совокупность дуг или ребер, которые соединяют все вершины графа, но не образуют ни одного цикла или контура.
Величина дерева определяется суммой его ветвей, то есть количеством ребер или дуг в него входящих. Если количество вершин обозначим через n, а количество дуг через m, то количество ветвей q=n-1.
Хорда – это ветвь графа, которую необходимо отбросить, чтобы получить дерево. Количество хорд в графе определяется как p=m-(n-1).
Ранг графа – это число хорд, входящих в этот граф.
Матричное описание графов.
1. Две вершины называются смежными, если существует дуга или ребро их соединяющая.
Матрица смежности для неориентированного графа определяется так:
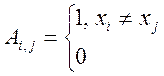
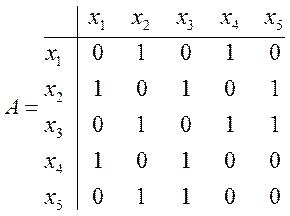
Свойства матрицы смежности.
- сумма элементов матрицы смежности в каждой строке равна степени соответствующей вершины.
- матрица смежности является симметричной относительно главной диагонали, с 0 на ней.
Для ориентированного графа.
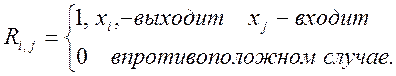
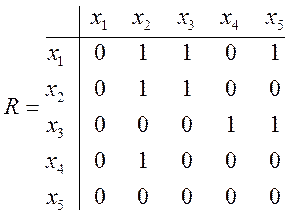
2. Вершина и дуга называются инцидентными, если дуга ее касается.
матрица инцидентности для неориентированного графа.
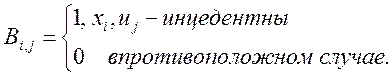
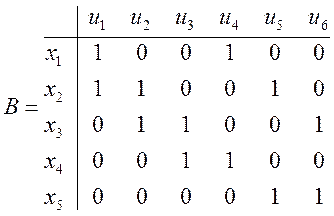
матрица инцидентности для ориентированного графа.
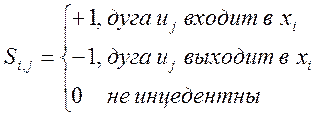
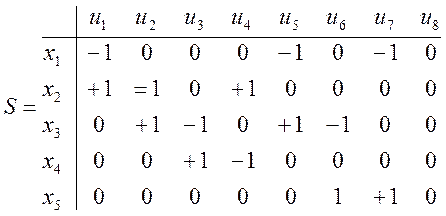
Свойства:
- сумма элементов каждого столбца матрицы равна 0.
- любой определитель, содержащийся в матрице должен быть равен 0,+1,-1.
- любой определитель матрицы инцидентности, соответствующий замкнутому контуру всегда равен 0.
Вопросы для самоконтроля.
1. Ориентированные графы.
2. неориентированные графы.
3. Алгоритмы оптимизации графов.
4. Составление матрицы смежности для графов.
5. Составление матрицы инцидентности для графов.
6. Сигнальные графы.
Цель. Изучить математическое описание дискретных динамических объектов.
Задачи:
1. Изучить понятия цифровых и импульсных систем.
2. Изучить математическое описание дискретных систем.
3. Рассмотреть способы квантования и модуляции сигналов.
4. Определить понятия решетчатой функции и разностных уравнений.
При математическом описании реальных систем управления необходимо описывать элементы являющиеся дискретными. В этих элементах входной сигнал изменяется не непрерывно, а скачками. В этом случае происходит квантование сигнала. Выделяют следующие виды квантования.
1). Квантование по уровню.

В этом случае амплитуда входного сигнала разбивается на равные интервалы. Исходная непрерывная функция x(t) заменяется последовательностью ленточных функций, зафиксированных на соответствующие уровни.
2). Квантование по времени.
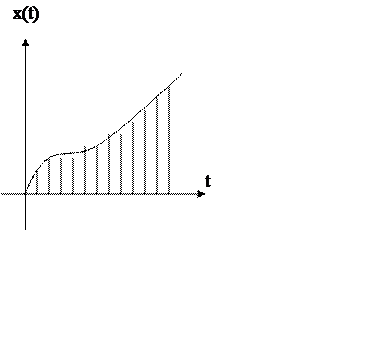
В этом случае на оси времени выделяются равные промежутки и исходная непрерывная функция заменяется последовательностью импульсов конечной длительности, площади которых совпадают со значением непрерывной функции в этот момент времени.
3). Цифровое квантование.

В этом случае исходная непрерывная функция заменяется набором приближенных значений, определенных в узлах сетки, построенной следующим способом: на оси времени откладываются равные промежутки на оси значений – функции, равные значениям амплитуды.
Элементы, в которых осуществляется квантование по уровню, называются релейными, соответственно САУ, содержащие такие элементы – релейные.
Элементы, в которых осуществляется квантование по времени, называются импульсными.
Элементы, осуществляющие квантование по уровню и по времени, называются цифровыми.
При математическом описании релейных и цифровых систем, используются нелинейные уравнения. При описании импульсных систем могут использоваться как линейные нелинейные, так и линейные уравнения. При исследовании систем, описываемых нелинейными уравнениями необходимо использовать или специальные методы анализа или приводить нелинейные уравнения к линейным, а затем исследовать их как линейные системы.
Рассмотрим импульсные системы. В них кроме импульсного элемента, содержится непрерывные элементы, которые можно объединить в непрерывную часть.

Импульсная модуляция заключается в изменении одного из параметров входного сигнала: амплитуды (А), времени импульса (t), периода следования импульсов (Т). В соответствии с этим различают амплитудно-импульсную, широтно-импульсную и частотно-импульсную модуляции.
1). Амплитудно-импульсная модуляция.
В этом случае время импульса и период следования являются величинами постоянными, а амплитуда – переменной.
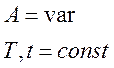
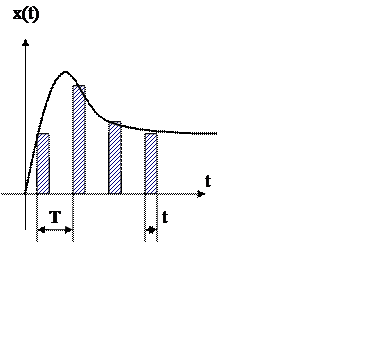
2). Широтно-импульсная модуляция.
В этом случае амплитуда импульса и период следования являются величинами постоянными, а время следования импульса – переменной.
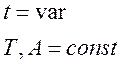
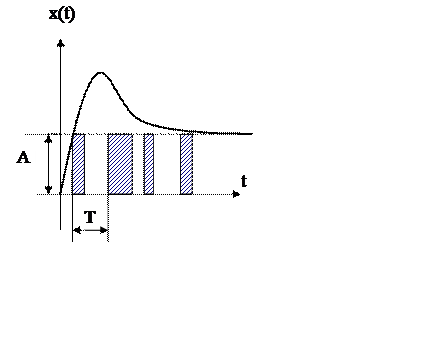
3). Частотно-импульсная модуляция.
В этом случае амплитуда импульса и время следования являются величинами постоянными, а период следования импульса – переменной.
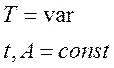
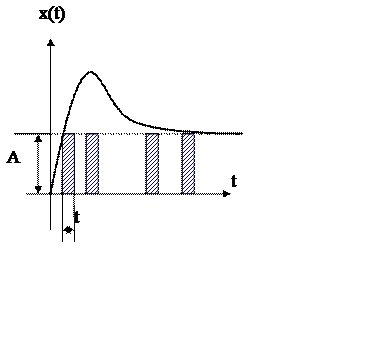
При различных видах модуляции, значению непрерывной функции пропорционально: амплитуда (АИМ);время (ШИМ);период (ЧИМ).
При использовании ЧИМ и ШИМ применяются нелинейные элементы, а при АИМ могут использоваться как нелинейные, так и линейные элементы, поэтому в дальнейшем дальше будем рассматривать амплитудно-импульсную модуляцию.
При АИМ импульсный элемент работает как некоторый ключ, замыкающийся на время импульса t, и в момент замыкания значение модулируемого сигнала совпадает со значением непрерывного сигнала и этот процесс повторяется с периодом Т. В том случае, когда t<<Т, последовательность получаемых импульсов можно представить в виде последовательности δ импульсов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.