Принцип работ, функции, алгоритм систем правления с отрицательной обратной связью, страница 8

1) Р/м электронный усилитель:                     ~ U_m

структурная схема имеет вид:

                                                           1мили В             ΔU_num                                  1В

 

                                                                                             ЭУ

К=U_вых./U_вход.=1В/10^-3В=1000

где К- коэффициент передачи

Подадим на вход синусоидальный сигнал U_вход.=1*10^-3 В sin ωt, на выходе получим U_вых.=1В sin ωt.

        2) Нас интересует стабильность работы усилителя при изменении

напряжение питания. Напряжение питания ~U_m=220 В±20 В

Достаточна ли стабильность усилителя при имеющихся колебаниях питания ?

Примем за U_вход. отклонение напряжения от 220 В

   Δ U_num                                     Δk

                            ЭУ           

В качестве выходного параметра будем р/м изменение коэффициента усиления. Проводим эксперименты, подадим синусоидальный сигнал и фиксируем выходные значения при различных напряжениях питания:

U₁=200 B            K₁    Получим коэффициенты передачи, по этим данным мы можем

U₂=200 B            K₂    построить зависимость коэффициента передачи от изменения

U₃=200 B            K₃    напряжения питания.

3) Р/м влияние температуры окружающей среды на стабильность усилителя.

 ΔТ⁰                                  Δk

На входе изменение температуры ΔТ⁰, на выходе Δk. Т.о. каждый элемент или процесс могут иметь множество математических моделей. Мы будем заниматься моделями преобразования входного сигнала в выходной( модель № 1)

1.  Функциональная зависимость y=f(x)

Каждому значению х соответствует одно значение у

y=b₀+bx

y=x²

                                                             y₁ 

 

y₂

                                                                                         x₂                                                                                         x₁

2.  Оперативная зависимость  y(t)=A*x(t) , где А- оператор

Каждой функции x(t) соответствует функция y(t), к ним относятся: дифференциальные уравнения, преобразование Фурье, Лапласа и др.

 Например:     н.у.             К и Т

 Т(dy/dt)+y=Kx            x(t)                                            y(t)

                                                                    ДУ

     Каждому виду x(t) соответствует своя функция y(t)

 

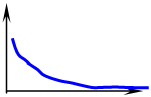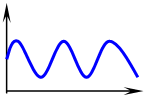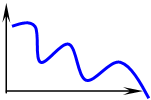                      а)                                                  б)                   в)

     3. Функцоинал       

x(t), y(t)                                       A- число

                         x₁(t)

I=₀∫^Tx(t) dt                                 При изменении вида функции, площадь изменяется

                                                                      x₂(t)

I₁=S₁=₀∫^Tx₁(t) dt                          t                                                I₂=S₂=₀∫^Tx₂(t) dt

                                              Т                                  T

                                   S₁                                                                   t                                   S₂

Дифференциальные уравнения 1-го порядка

При изучении закономерностей процессов часто не удается найти закон, связующий выходные переменные с входными. Но возможно установить зависимость между переменными, их производными и дифференциалами. Получаем при этом уравнение, содержащее функции, их производные или дифференциалы, такие уравнения называются дифференциальными. Нахождение неизвестных уравнений, определенных дифференциальными есть задача, теория дифференциального уравнения. Задачами анализов системы является: определение закономерности изменения выходного сигнала элемента во времени y(t) при заданном законе входного сигнала x(t). Как указано выше такие связи часто описываются дифференциальными уравнениями:

     x(t)                          y(t)

                      ДУ

 a_n*(d ⁿ y(t)/dt ⁿ)+ a_n-1*(d ^n-1 y(t)/dt ^n-1)+… a₂*(d ² y(t)/dt ²)+ a₁*(d ¹ y(t)/dt ¹)+ a₀ y(t)=

b_m*(d^mx(t)/dt^m)+ b _m-1*(d ^m-1 x(t)/dt ^m-1)+… b₂*(d² x(t)/dt²)+ b₁*(d¹x(t)/dt¹)+ b₀ x(t)- линейное дифференциальное уравнение n- го порядка, причем m ≤ n.

линейное дифференциальное уравнение 1- го порядка:

a₁*(d ¹ y(t)/dt ¹)+ a₀ y(t)= b₀ x(t)

линейное дифференциальное уравнение 2- го порядка:

a₂*(d ² y(t)/dt ²)+ a₁*(d ¹ y(t)/dt ¹)+ a₀ y(t)= b₀ x(t)

Уравнения 1-го и 2-го порядка описывают многие известные из жизни закономерности.

Пример: р/м схему № 1   структурная схема                   математическая модель

                         R₁

                                                                                   x(t)                 _ММ           y(t)

                                                                                  U₁(t)                                 U₂(t)

       U₁(t)         i                      R₂                   U₂(t)

На основании известных законом Ома и Кирхгофа, составим уравнение связи U₁(t) и U₂(t).

U₂=iR₂                    

                             => U₂= U₁* R₂ /(R₁+R₂)  т.к. R₂ /(R₁+R₂)=k  то U₂=k* U₁

i=U₁/(R₁+R₂)    

при R₁=R₂         k=0,5

Построим зависимость U₂(t) от U₁(t).

y(t)=kx если на вход делителя подавать напряжение по закону №1, то на выходе получим закон №2, причем закон №2 имеет тот же вид, только напряжение в два раза меньше.

          U₁                                                                       U₂

    30

    25

    20

    15

    10

     5

                                                            t                                                           t