При определении решетчатой функции ![]() следует оговорить
следует оговорить
![]() или
или
![]() .
.
Будем считать предел справа, т.к. импульсный элемент формирует именно правое значение.
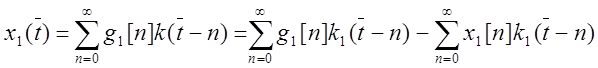
Полагая ![]() ,
окончательно находим:
,
окончательно находим:
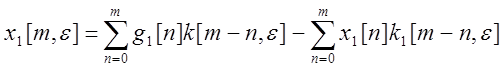 .
.
Для определения ![]() нужно это уравнение решить, что
возможно, например, с помощью дискретного преобразования Лапласа.
нужно это уравнение решить, что
возможно, например, с помощью дискретного преобразования Лапласа.
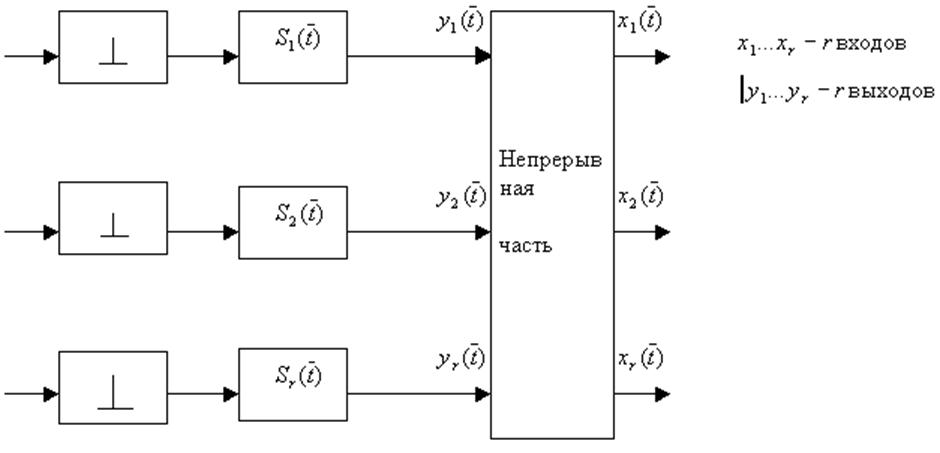 |
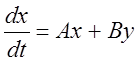
Все импульсные элементы работают синхронно и синфазно.
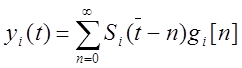 ,
,
![]()
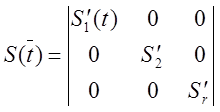
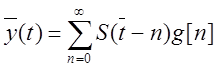
Пусть ![]() -
фундаментальная матрица.
-
фундаментальная матрица.
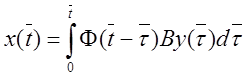 ,
при x(0)=0
,
при x(0)=0
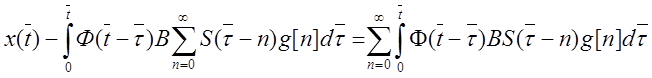
![]()
![]() ,
,
![]()
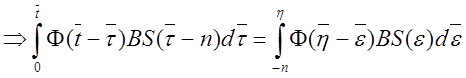 .
.
Матрица ![]() ,
при
,
при ![]()
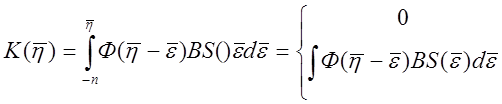
![]()
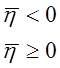
Тогда уравнение импульсной системы можно представить как
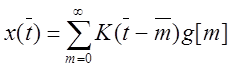 или полагая
или полагая ![]()
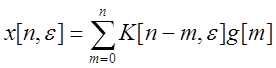
![]() -уравнение ошибки
-уравнение ошибки
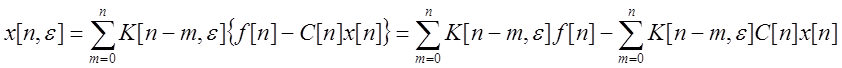
Z - преобразование.
Определение и условие существования.
Z-преобразование рассматривается применительно к сигналу с импульсной модуляцией.
![]() при
при ![]() <0,
<0,
![]()
 <
<![]() –
условие достаточное, но не необходимое. Если выбрать значения g(t) при t=nT,
то существует
–
условие достаточное, но не необходимое. Если выбрать значения g(t) при t=nT,
то существует 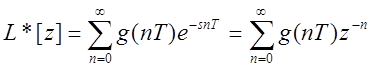 , где z=e
, где z=e![]()
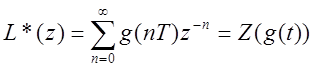
Это выражение с точностью до множителя T является полной аналогией непрерывного преобразования.
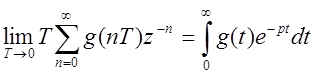 , так как dt=T, а nT=t,
поэтому дискретное преобразование Лапласа называют ещё обобщённым
преобразованием.
, так как dt=T, а nT=t,
поэтому дискретное преобразование Лапласа называют ещё обобщённым
преобразованием.
Пример: ![]() ,
, 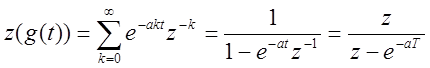
Геометрическая
прогрессия: an=a1qn-1; Sn=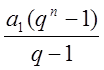 ;
; 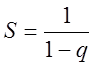
![]() - z-преобразование
для непрерывной функции.
- z-преобразование
для непрерывной функции.
![]() - z-преобразование
для непрерывной функции с запаздыванием.
- z-преобразование
для непрерывной функции с запаздыванием.
В более общем
виде условия существования z-преобразования для
дискретной функции ![]() ,
, ![]() ,
где n<0.
,
где n<0.
 Нетрудно
доказать сходимость ряда
Нетрудно
доказать сходимость ряда 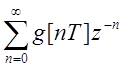 : Рассмотрим ряд
: Рассмотрим ряд 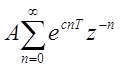 , представляющий геометрическую
прогрессию со знаменателем
, представляющий геометрическую
прогрессию со знаменателем ![]() , которая
сходится при q<1 или
, которая
сходится при q<1 или ![]() и
его сумма равна
и
его сумма равна 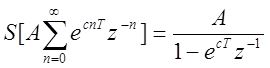 . Но каждый член
. Но каждый член ![]() , где
, где ![]() =R=ecT – радиус сходимости.
=R=ecT – радиус сходимости.
Связь z-преобразования с преобразованием Лапласа.
![]() - аналитическая дискретная функция.
- аналитическая дискретная функция.
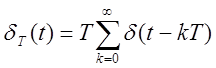 - дельта Функция.
- дельта Функция.
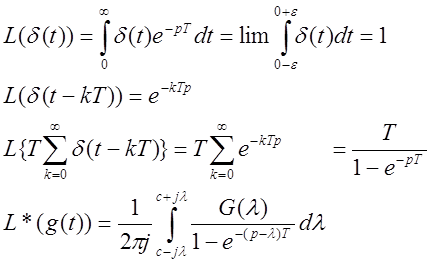
Эта формула устанавливает связь между преобразованием Лапласа для непрерывной функции и соответствующим z-преобразованием.
Прямая
интегрирования должна лежать правее полюсов G(λ) и левее 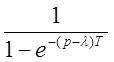 . Равенство
справедливо при Re p>c0 – абсцисса
абсолютной сходимости.
. Равенство
справедливо при Re p>c0 – абсцисса
абсолютной сходимости.
Вычислим интеграл с помощью вычетов.
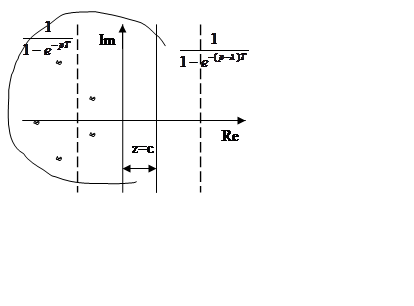 Полюсы
подынтегральной функции внутри контура интегрирования будут совпадать с
Полюсы
подынтегральной функции внутри контура интегрирования будут совпадать с 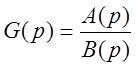 ,
, 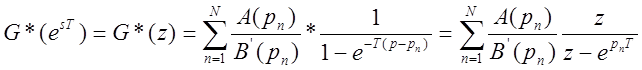 ;
z=epT
;
z=epT
С помощью этой формулы удобно определить z-преобразование по известному преобразованию Лапласа непрерывной функции.
Определение оригинала по известному z-преобразованию.
g(kT)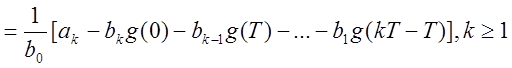
Если k>n и i >n , то в этой формуле все bi при i>n и ak пропадут:
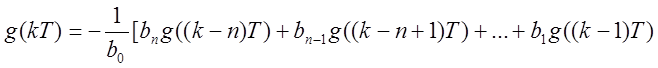
Эти формулы позволяют, не производя каждый раз деления, определять дискретные значения функции оригинала для дробно-линейных преобразований z. Формулы очень удобны для вычислений и могут быть использованы для вычисления переходных процессов в непрерывных системах.
Теорема Котельникова.
Устанавливает эквивалентность непрерывного и дискретного сигналов.
Точная формулировка теоремы применима к непрерывным сигналам со спектром, ограниченным по частоте.
Допустим, что
имеем непрерывный сигнал g(t),
спектр которого G(ω) равен нулю
при ![]()
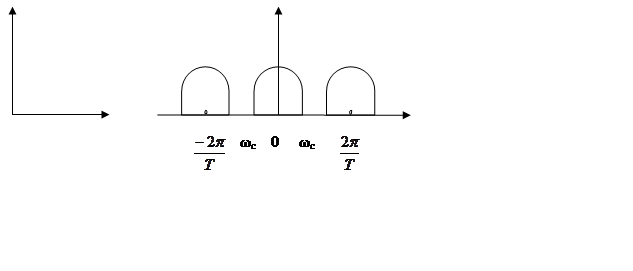
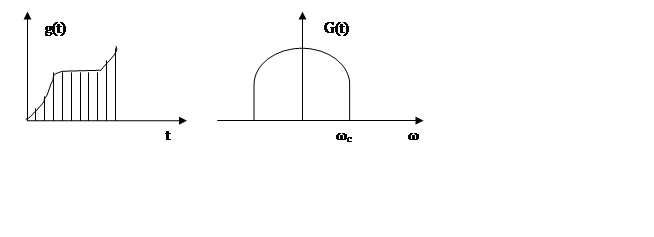 Возможны 3
случая:
Возможны 3
случая:
1.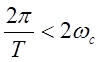
2.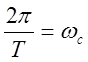
3.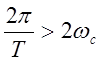
при 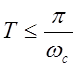
Определение и свойства преобразования с запаздыванием.
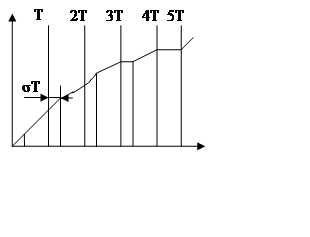
![]()
При σ→0 z-преобразование переходит в обычное z-преобразование.
1.![]()
2.![]()
3. ![]()
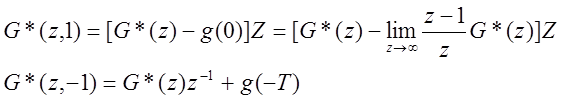
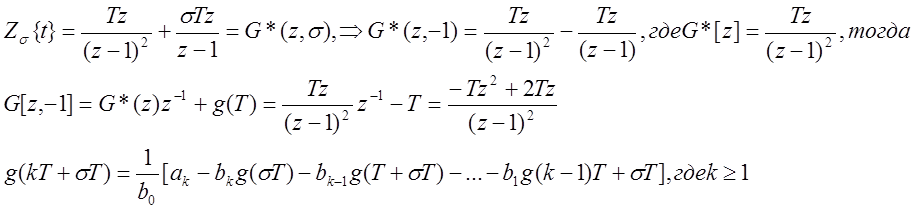
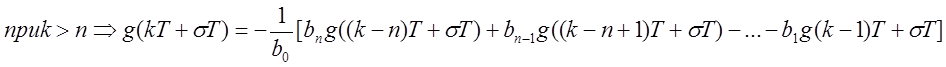
Определения и свойства w-преобразования.
z=epT – замена
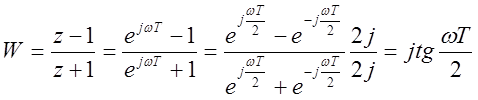
wz+w=z-1![]() w+1=z(1-w)
w+1=z(1-w) ![]()
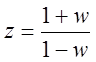
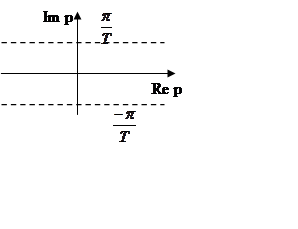 и тогда e-at
и тогда e-at![]()
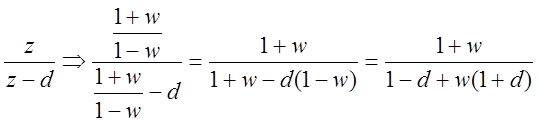
Некоторые теоремы z-преобразования.
Теорема линейности.
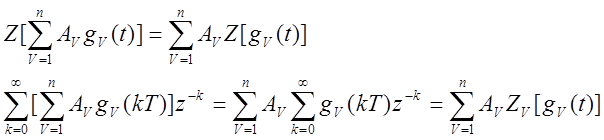
Теорема о начальном значении.
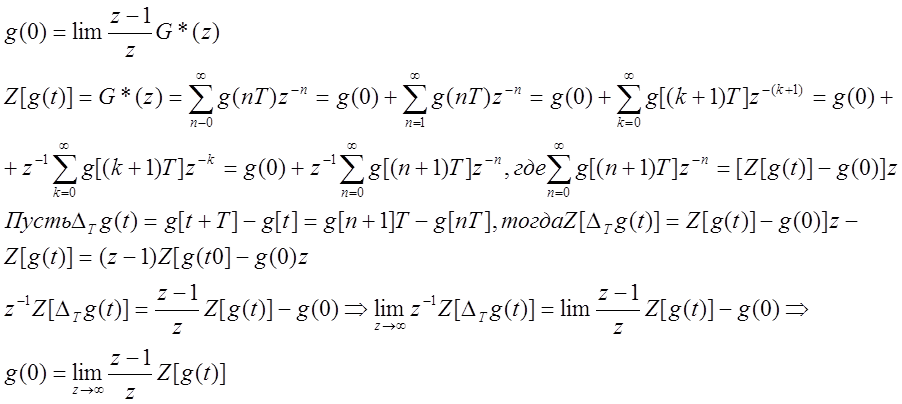
Теорема о конечном значении.
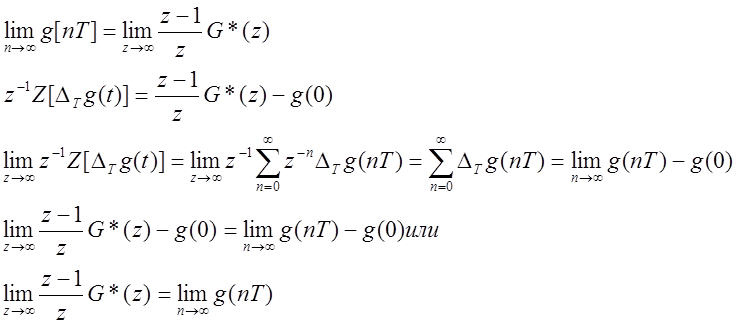
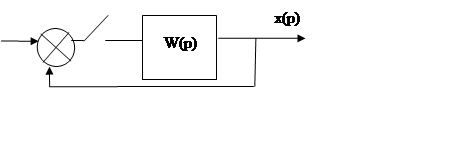
Передаточные функции.
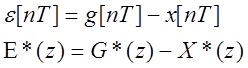
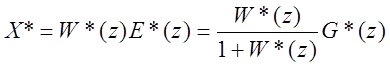
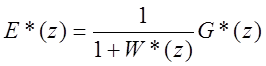
Заметим, что
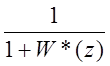 – не является z-преобразованием,
соответствующим
– не является z-преобразованием,
соответствующим 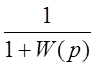 , хотя
, хотя ![]()
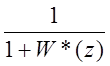 =
=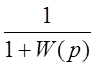 .
.
Передаточные функции:
Φ*(z)= 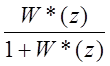 - по выходному
сигналу;
- по выходному
сигналу;
Φε*(z) = 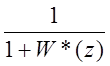 - по ошибке;
- по ошибке;
С помощью этих передаточных функций выходной сигнал и сигнал ошибки в дискретные моменты времени могут быть вычислены по формулам:
![]()
![]()
Если выражения разложить в ряд по z-n , то получим X(nT) и, соответственно, E(nT).
Для нахождения сигнала в любой момент времени необходимо ввести запаздывание.
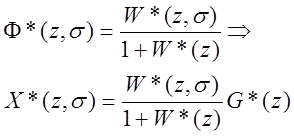
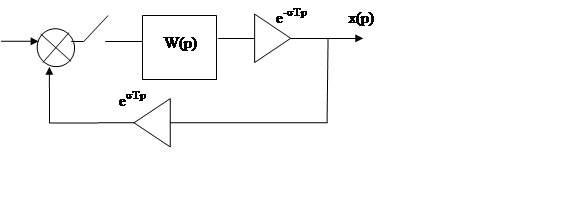
Дифференцирующий цифровой фильтр.

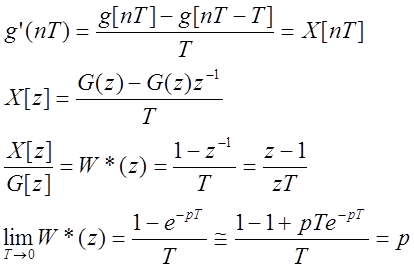
Частотные характеристики непрерывного и цифрового дифференциаторов.
Если требуется более точное дифференцирование, то необходимо использовать более точную формулу:
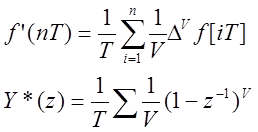
Цифровые интеграторы.
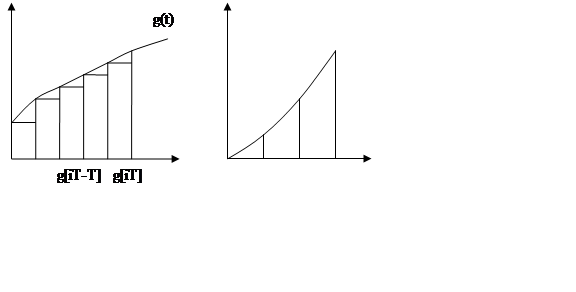 В простейшем
случае :
В простейшем
случае :
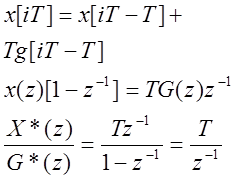
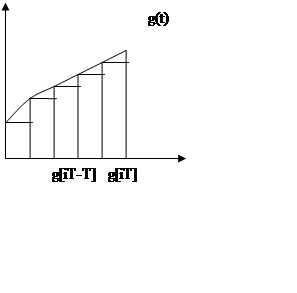 Можно
осуществить более точное численное интегрирование:
Можно
осуществить более точное численное интегрирование:
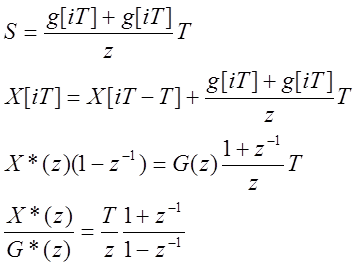
Сравнение двух методов показывает, что:
1. объём памяти одинаков;
2. во втором случае больше на одну операцию суммирования.
Устойчивость дискретных следящих систем.
Определение устойчивости.
Дискретную систему будем называть устойчивой, если при ограниченном входном сигнале выходной сигнал также ограничен.
Если g(iT)<M , то x(iT)<M1
Для дискретной
системы необходимым и достаточным условием устойчивости является ограниченность
суммы 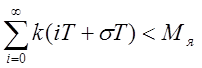 для всех σ:
для всех σ:
![]()
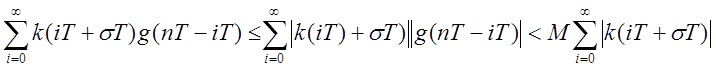 -
достаточность
-
достаточность
Для устойчивости дискретной следящей системы необходимо и достаточно, чтобы все корни знаменателя передаточной функции были расположены внутри единичного круга.
Алгебраический критерий устойчивости Шур-Кона.
В теории полиномов существует критерий отсутствия корней по модулю больших единицы.
![]()
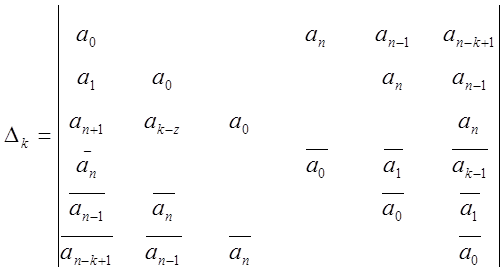
Если все детерминанты
отличны от нуля, то этот полином не имеет нулей на окружности ![]() и N его
нулей расположены вне этой окружности, причём N равно
числу перемен знаков в последовательности: 1, Δ1, Δ2…, Δn.
и N его
нулей расположены вне этой окружности, причём N равно
числу перемен знаков в последовательности: 1, Δ1, Δ2…, Δn.
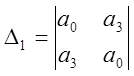
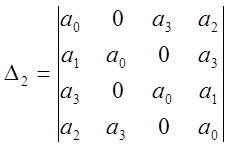
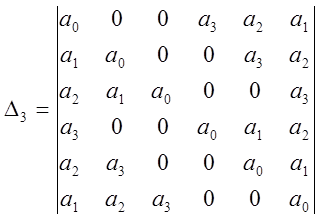
Пример:![]() , если n=2, a0=1,
a1=A, a2=И
, если n=2, a0=1,
a1=A, a2=И
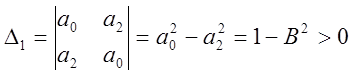
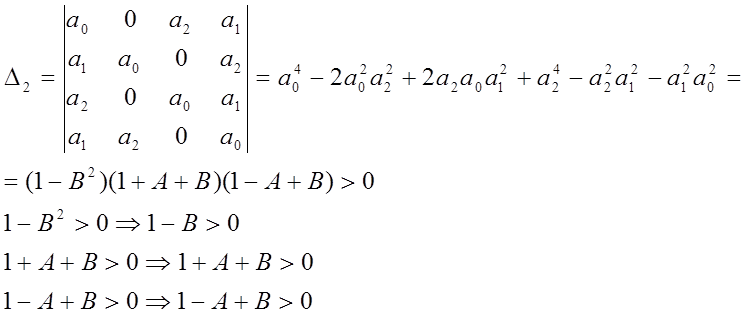
Частотные критерии устойчивости.
Пусть 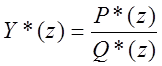 и
и 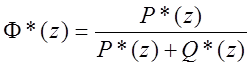 где
где
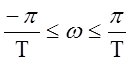 ,
, ![]() .
.
Для
устойчивости дискретных систем достаточно, чтобы годограф знаменателя
передаточной функции замкнутой системы охватывал начало координат n раз, где n- степень полинома.
Разность между степенью полинома и числом оборотов годографа вокруг начала координат
даёт порядок неустойчивости, т. е. число ![]()
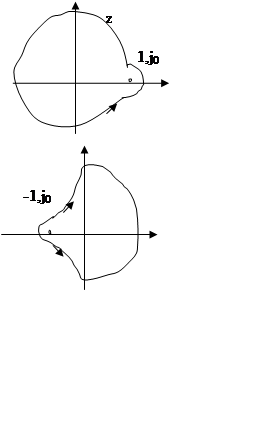
Для определения устойчивости замкнутой системы по годографу устойчивой разомкнутой системы достаточно, чтобы годограф передаточной функции разомкнутой системы не охватывал точку (-1,j0).
Число оборотов
годографа вокруг этой точки равен порядку неустойчивости системы, т. е. числу
корней k, ![]() .
.
1. Годограф любой системы начинается на действительной оси :
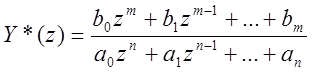
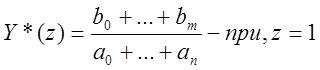
2.  Если Y*(z) имеет полюс z=1:
Если Y*(z) имеет полюс z=1:
![]()
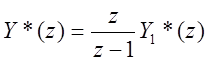
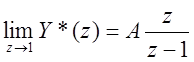
при ![]()
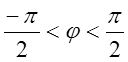
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.