![]() - матрица усиления контура
- матрица усиления контура
r-y2 – ошибки системы управления.
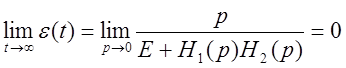
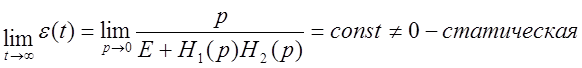 |
при условии, что ![]()
Система является статической, т.е. имеет ошибку в установившемся
состоянии, если числитель и знаменатель функции 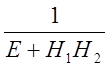 имеют
свободные члены не зависимые от p.
имеют
свободные члены не зависимые от p.
Если же функция 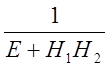 имеет нуль
какого-либо порядка при p=0, то система является
астатической первого порядка.
имеет нуль
какого-либо порядка при p=0, то система является
астатической первого порядка.
Система имеет астатизм порядка n, если передаточная функция имеет нуль порядка n.
Пусть ![]()
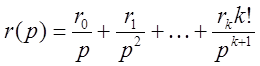
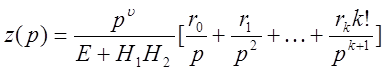
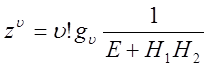
Передаточная функция 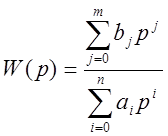
Каждый полином (числитель и знаменатель) может быть представлен в виде разложения на простые множители
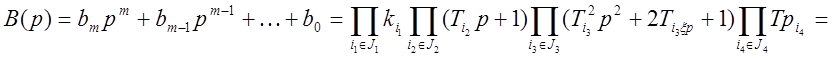
![]()
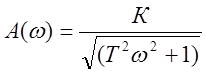
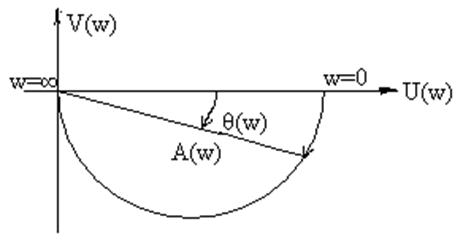 |
![]()
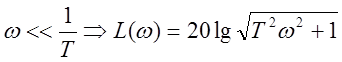
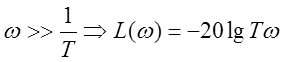
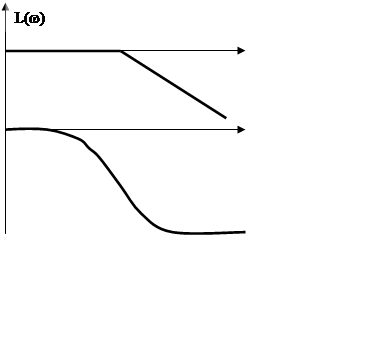
Наклон ![]()
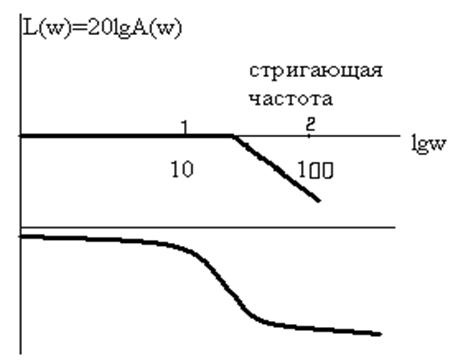 |
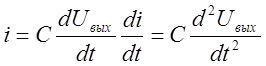 |
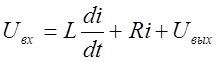
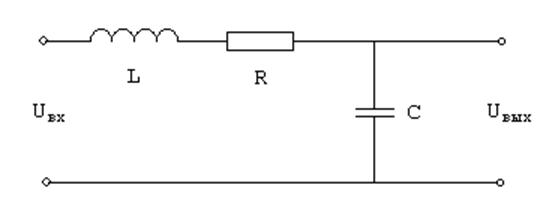 |
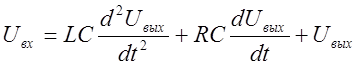
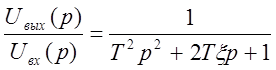
LC=T2 RC=2Tx 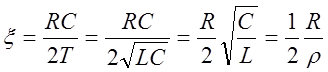
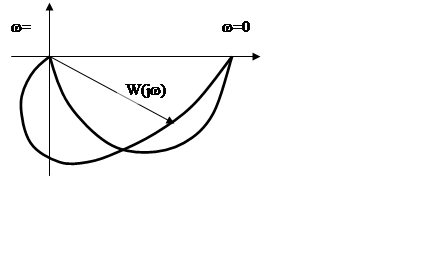 Частотная характеристика
Частотная характеристика
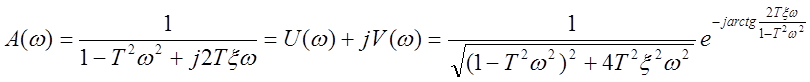
Корни
характеристического уравнения 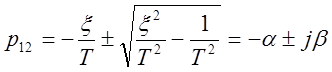
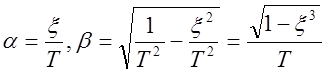
Если x=0, то a=0 b=1/T=w0
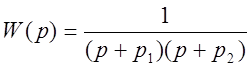
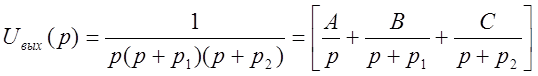
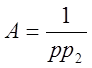
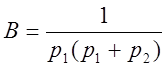
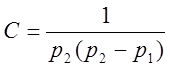
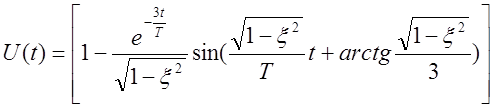
![]()
![]()

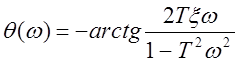
1) 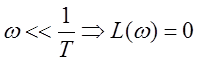
 2)
2) 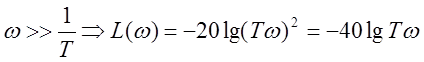
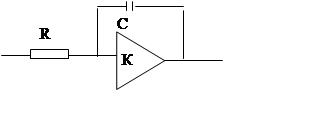 Интегрирующее звено
Интегрирующее звено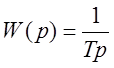
Uвх=Ri, 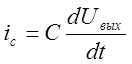 ,
,
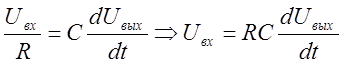
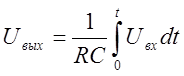
![]()
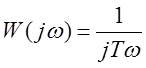
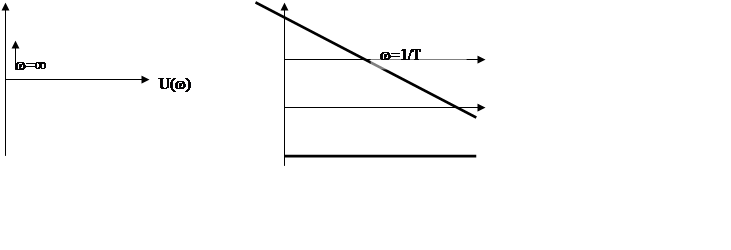 |

W(p)=Tp
W(j![]() )
)![]() ,
h(t)=Td(t)
,
h(t)=Td(t)
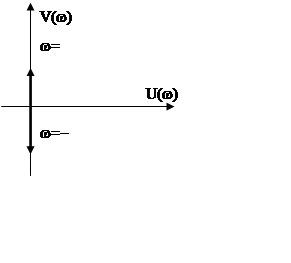
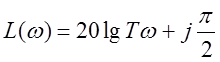
W(p)=Tp+1
W(jw)=jTw+1
![]()
![]()
![]()
W(jw)=k, L(w)=k
![]()
Задача: Рассмотрение поведения дифференциальных уравнений на длительном интервале времени.
Пусть уравнение состояния имеет вид ![]() .
.
Исследовать будем ![]() при
u(t)=0, x0(t) – номинальное решение
при
u(t)=0, x0(t) – номинальное решение ![]()
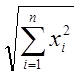
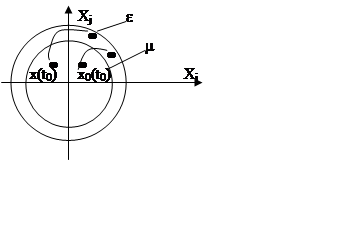 |
Определение: номинальное решение x0(t) уравнения состояния x¢(t) является асимптотически устойчивым, если
А) оно устойчиво по Ляпунову
Б) "t0
существует r(t0)>0
такое, что при êêx(t0)-x0(t0)êê<r(t0) 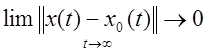
Определение: Номинальное решение x0(t) уравнения состояния ![]() является
асимптотически устойчивой в целом (большом), если оно
является
асимптотически устойчивой в целом (большом), если оно
А) устойчиво по Ляпунову
Б) для любого и "t0 êêx(t)-x0(t)êê®0 при t®¥
Три условия (случая):
Для нелинейных систем Þ
устойчивость решений, а для линейных -устойчивость систем, т.к. если ![]() и
и ![]() , то
, то ![]() .
.![]()
Определение: линейная динамическая система устойчива в определенном смысле (по Ляпунову, асимптотически как в малом так и большом), если травиальное решение устойчиво в этом смысле x0(t)º0.
Теорема. Линейная динамическая система ![]() асимптотически
устойчива тогда и только тогда, когда она асимптотически устойчива в целом.
асимптотически
устойчива тогда и только тогда, когда она асимптотически устойчива в целом.
Теорема следует из безусловной продолжаемости решений.
Теорема: линейная динамическая система с переменными параметрами ![]() является экспоненциально устойчивой,
если существуют положительные константы a
и b такие, что
является экспоненциально устойчивой,
если существуют положительные константы a
и b такие, что ![]() "t>t0.
"t>t0.
Устойчивость линейных систем с постоянными параметрами.
![]()
![]()
![]()
![]()
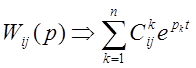
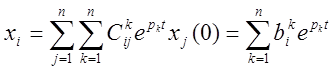 , где
, где 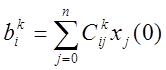
Теорема: Линейная система с постоянными параметрами ![]() является устойчивой в смысле
Ляпунова тогда и только тогда, когда
является устойчивой в смысле
Ляпунова тогда и только тогда, когда
А) все характеристические числа А имеют неположительные действительные части.
Б) любому характеристическому числу на мнимой оси кратности m точно соответствует m собственных векторов матрицы А.
Теорема: Динамическая система с постоянными параметрами ![]() является асимптотически устойчивой
тогда и только тогда, когда все характеристические числа матрицы А имеют строго
отрицательные действительные части.
является асимптотически устойчивой
тогда и только тогда, когда все характеристические числа матрицы А имеют строго
отрицательные действительные части.
Например:
1.Смесительный бак.
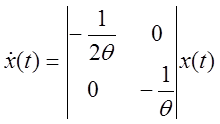 : x1(t)=x1(0)e
: x1(t)=x1(0)e![]() , x2(t)=x2(0)e
, x2(t)=x2(0)e![]()
2. Перевернутый маятник
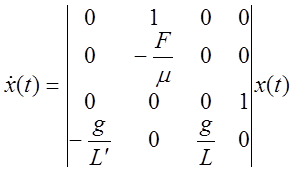 ,
, 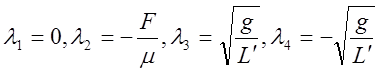
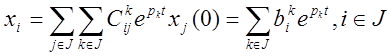
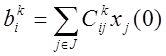
Пусть k={1¸m}=M, êJê=êMê+êJ-Mê
m-количество характеристических чисел матрицы А с
неотрицательной действительной частью матрицы А ![]()
n-m- количество характеристических чисел с отрицательными корнями.
Тогда подпространство RmÎRn
будет подпространством неустойчивых состояний![]()
![]()
Постановка задачи: определение свойств динамической системы (функции ее
параметров), при которых осуществим перевод системы из произвольного состояния x(0) в произвольное состояние ![]() ,
,
![]() .
.
Определение : линейная динамическая система ![]() будет
полностью управляемой , если ее можно перевести из х(0) в х(1) за время
будет
полностью управляемой , если ее можно перевести из х(0) в х(1) за время ![]() .
.
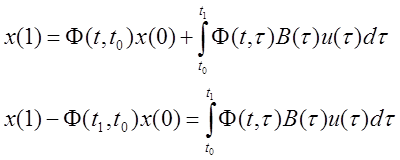
![]() новое конечное состояние.
новое конечное состояние.
Теорема. Линейная динамическая система полностью управляема, если она
может быть переведена из начала координат в состояние х(1) за конечное время (![]() ).
).
Пример: смесительный бак имеет равные входные концентрации![]() . Приращение концентрации С в
этом случае неуправляемо.
. Приращение концентрации С в
этом случае неуправляемо.
Теорема: Линейная динамическая система ![]() полностью
управляема, если матрица Р=(В, АВ, А2В, …, Аn-1В)
порождает n-мерное пространство.
полностью
управляема, если матрица Р=(В, АВ, А2В, …, Аn-1В)
порождает n-мерное пространство.
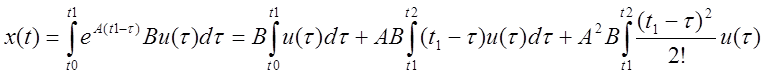
В последовательности матриц В, АВ, А2В должна появиться матрица АlВ=ВL0+АВL1+…+Ад-1ВLl и далее Аl+1В=АВL0+АВL1+…+АlВLl. Вектор-столбцы матрицы АlВ линейно зависят от вектор-столбцов матрицы В АВ А2В …Аl-1В.
х(t1)-принадлежит линейному подпространству, порожденному вектор-столбцами АВ.
Если эти вектор-столбцы не порождают n-мерное пространство можно достичь только состояний меньшей размерности, поэтому система не является полностью управляемой. Если система полностью управляема, вектор-столбцы матрицы Р порождают n-мерное пространство.
Положим, что Р порождает n-мерное пространство.
Тогда выбрав u(t) в коэффициентах
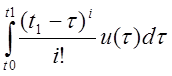 , можно получить,что любому вектору
, можно получить,что любому вектору
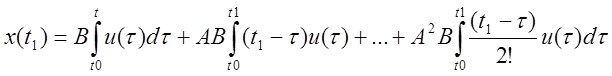 будет удовлетворять указанное
равенство
будет удовлетворять указанное
равенство
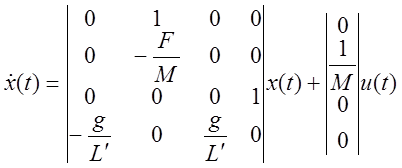
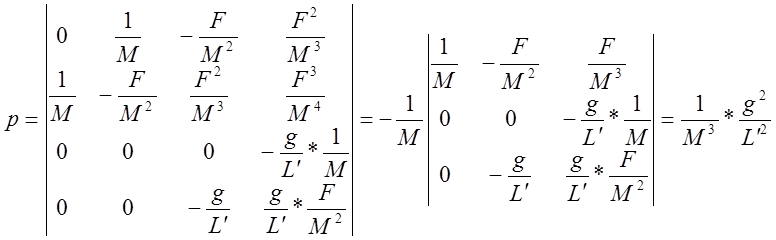
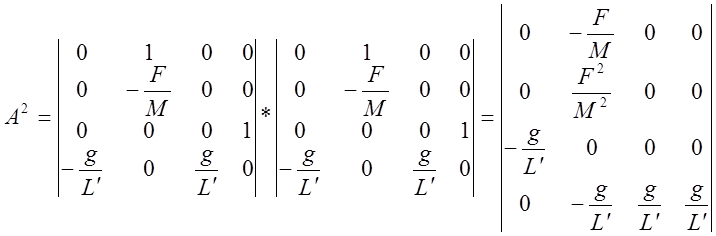
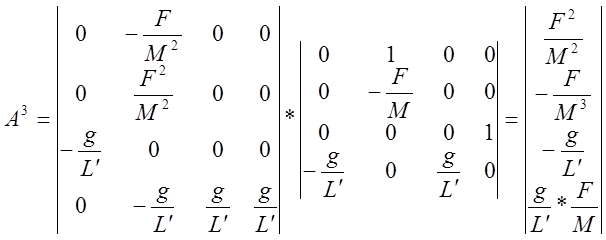
Подпространство управляемых состояний.
Лемма. Если вектор х принадлежит подпространству управляемых состояний, то вектор Ах также принадлежит этому подпространству
![]()
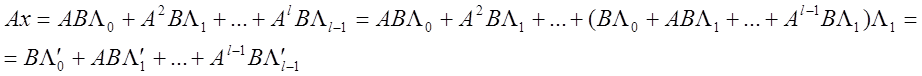
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.