Применение автоматов в современных технических системах, страница 4

Теорема. Линейная динамическая система переходит из состояния х₀ в состояние х₁, принадлежащих пространству управляемых состояний, за конечное время t₁

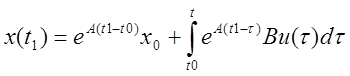
х₀- принадлежит пространству управления.

 - принадлежит пространству упрвления на основании свойства инвариантности

 - принадлежит , т.к х₁ и е^A(t1-t) тоже принадлежит.

            Формула показывает, что система переводится из нулевого состояния в  за конечное время, что тоже самое из х₀ в х₁.

            Пусть rank P=m.

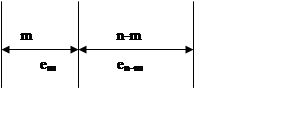е_m – линейно-независимые столбцы управления

Т₁=(е₁…е_m), T₂=(e_m+1…e_n).

Введем

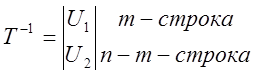
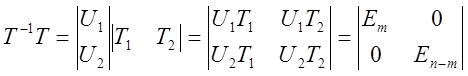
U₂T₁=0

T₁ состоит из е₁…е_m порождающих пространство управляемых состояний, следовательно, U₂x=0.

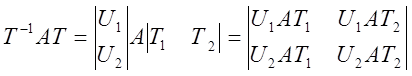
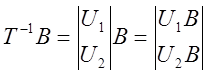
T_1, АТ₁ – принадлежит пространству управляемых состояний

U₂AT₁=0

B – часть матрицы управляемости и принадлежит пространству управляемых состояний

U₂B=0

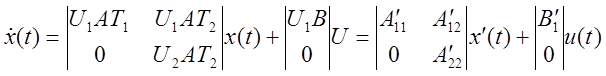- каноническая форма управляемости

-матрица m*m

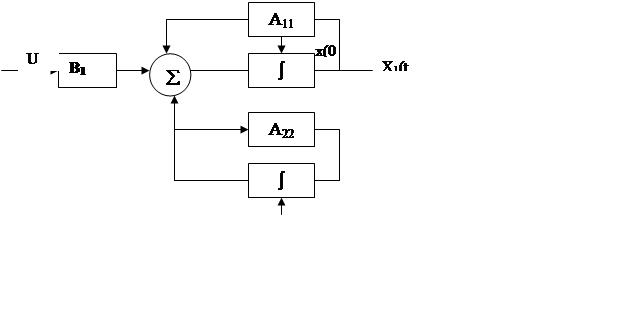
-полностью управляемая пара. Поведение системы -полностью независимо.

 

X2(0)

Смесительный бак

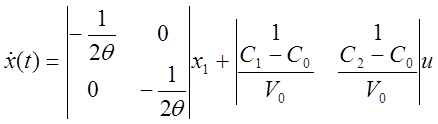
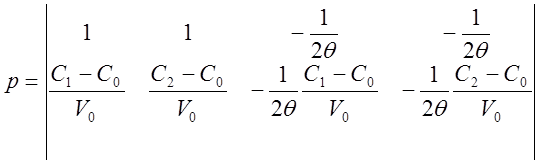
если С₁=С₂=С, то С₀=С

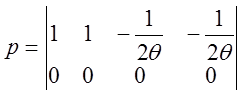
Наблюдаемость.

Пусть y(t,t₀,x₀,u) является выходной функцией линейной динамической системы  изменяющейся от начального состояния x(t₀). Система называется полностью наблюдаемой, если для всех t_i существует такой момент t₀, где  - ¥ <t₀ <t₁, что из равенства y(t,t₀,x₀,u)=y(t,t₀,x¢₀,u),  t₀£t £t₁ , для всех  u(t)    t₀£t £t₁  следует   x₀=x¢_0.

Теорема:

Система  y=Cx, является полностью восстанавливаемой в том и только в том случае, если для всех  t_i   существует такой момент  t₀         - ¥<t₀  <t₁, что из равенства  y(t,t₀,x₀,0)=0     t₀£ t £t₁  следует x₀=0

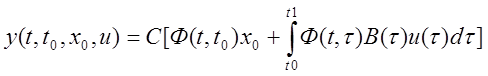
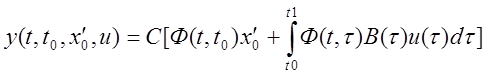
СФ(t,t₀)x₀=CФ(t,t₀)x¢₀ , x₀=x¢₀, СФ(t,t₀)(x₀-x¢₀)=0

Наблюдаемость означает, что имеется возможность определения состояния в момент t₀  по будущим значениям выходной переменной.

Линейная динамическая система  полностью наблюдаема (восстанавливаема), если rank матрицы

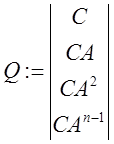 равен n.

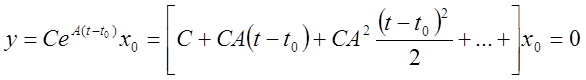
Если матрица Q не имеет полного ранга, то существует такое x₀ ,что:

Сx₀=0     CAx₀=0   …..  CA^(n-1) x₀=0.

Используя теорему Кели-Гамильтона, получим      СА^L x₀ =0, где   L ³n.

Докажем другое утверждение теоремы:

y(t₀)=Cx₀=0  или  Qx₀=0

y¢(t₀)=CАx₀=0

…………………...

y^(n-1)(t₀)=CA^(n-1) x₀=0

Если Q не имеет полного ранга, то равенства не будет.

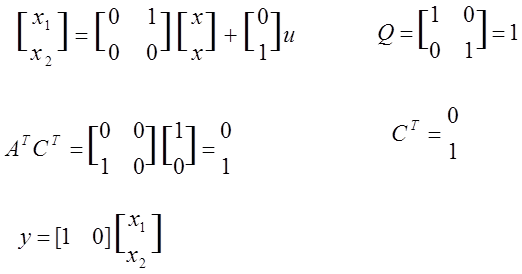
Пример:

Rank=2.

Критерий устойчивости линейных динамических систем.

Постановка задачи: рассмотрение фундаментального решения 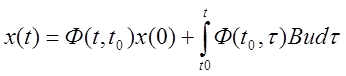динамической системы  показало его устойчивость, если действительные части характеристических чисел матрицы А отрицательны.

Определение (прямое) характеристических чисел-процесс трудоёмкий, но не безнадёжный.

Возникает задача: определение отрицательности характеристических чисел матрицы А по самим коэффициентам матрицы А.

Предварительные замечания.

Рассмотрим характеристическое уравнение: .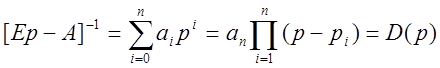

Введём вектор р=jw и рассмотрим 2 случая:

1.  Имеем вектор a_i=jw-p_i, где p_i=-a+jb.

Изменим вектор jw от -j¥ до + jw.

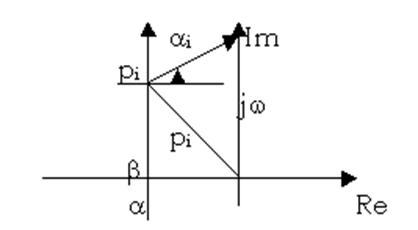Arg_jw=-j¥ a_i=-p/2,  DArga_i=p

Arg_jw=+j¥ a_i=p/2.

2.Имеем вектор  a_i=jw-p_i , p_i=a+jb, Arg _jw=-j¥ a_i=3p/2, Arg _jw=j¥ a_i=p/2, DArga_i=-p

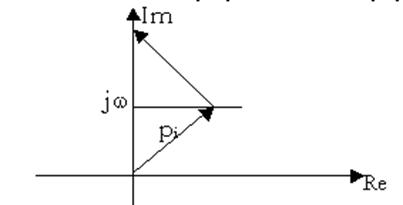            Рассмотрим D(jw)=Mod D(jw)e ^jArgD(jw)

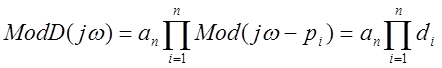
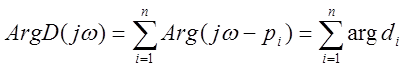
Теорема:

Изменение аргумента D(jw) при возрастании w от  -¥  до  +¥  равно разности между числом (n-m) корней уравнения D(jw)=0, лежащих в левой и правой полуплоскостях, умноженной на p, т.е.    (n-m)p-mp.

Критерий устойчивости Михайлова: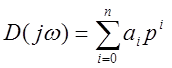

Если все корни отрицательны, то  "р_i : Reр_i<0 Þ  Darg D(jw)=np

D(jw)=u(w)+jv(w), где u(w)=а₀–а₂w²+а₄w⁴-…..

                                v(w)=а₁–а₃w³+а₅w⁵-…..

Так как u(w)- функция четная, а v(w)-функция нечетная, то D(jw)=-D(jw), т.е. годограф D(jw) симметричен относительно действительной оси.

Cистема автоматического управления устойчива, если при возрастании w от 0 до ¥ вектор D(jw) повернётся на угол np/2, где n-степень полинома D(jw)=0 или его годограф обходит последовательно в положительном направлении n квадрантов.

Система находится на границе устойчивости, если характеристическая кривая проходит через начало координат.

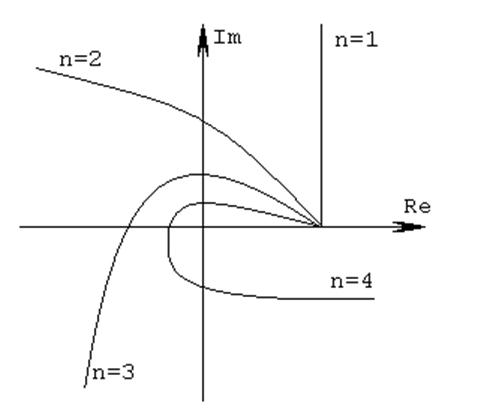Критерий устойчивости Раусса-Гурвица.

Основное соотношение, определяющее устойчивость DArg_0<w<¥D(jw)=np

u(w)=±(а₀wⁿ–а₂w^n-2+а₄w^n-4-...+ а_n)

v(w)=±(а₁w^n-1–а₃w^n-3+а₅w⁵-…+а_n-1w),              D(jw)=åа_ip^n-1.

Для того, чтобы система D(jw) была устойчивой, необходимо и достаточно, чтобы все главные определители определителю Гурвица были положительны.

Частотный критерий устойчивости Найквиста-Михайлова.

Имеем систему

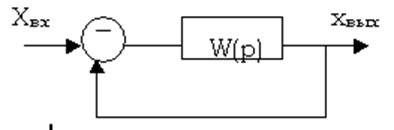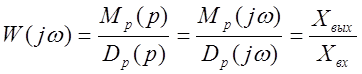
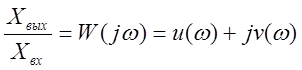
Введём функцию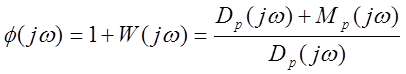

D(jw)=D_p(jw)+M_p(jw)

DArg_0<w<¥D(jw)=(n-2m)p/2

DArg j(jw)=DArg D(jw)-DArg D_p(jw)=(n-2m)p/2-np/2=-mp.

Система будет устойчива, если изменение аргумента DArg j(jw)=0, т.е. если годограф характеристики j(jw) не охватывает начало координат.

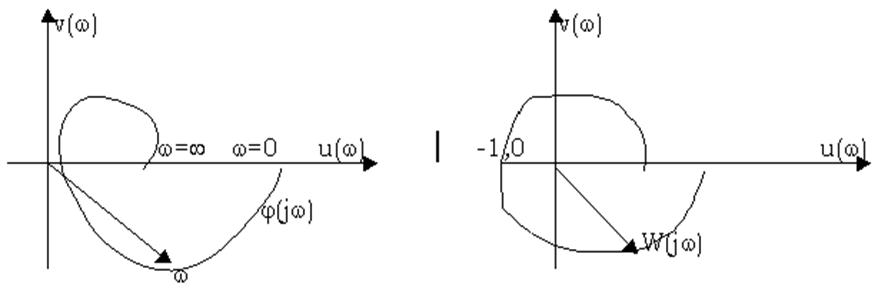Но W(jw)=j(jw)-1, т.е. замкнутая система устойчива, если частотная характеристика разомкнутой системы не охватывает точку (–1,0) при изменении 0<w<¥.

            Если разомкнутая система неустойчива, то DargD_p(jw)=(n-2p)p/2

            Если замкнутая система устойчива, то Darg j(jw)=DargD(jw)-D_p(jw)=n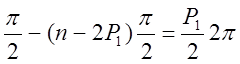

            Замкнутая система будет устойчива, если частотная характеристика неустойчивой разомкнутой системы охватывает т.-1,0 в положительном направлении Р₁/2 раз, где Р – число неустойчивых корней.

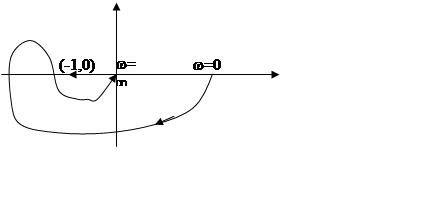
Запас по амплитуде и запас по фазе.

            j - запас по фазе ½j½

            20lg(1-A) – запас по амплитуде при проектировании не менее 6 дб.

 

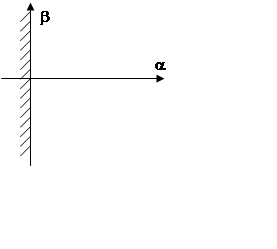
D-разбиение пространства параметров

            Комплексное пространство, мнимая ось которого разделяет его на два полупространства: слева устойчивое, справа – неустойчивое.

D(p)=D_p(p)+M_p(p) – характеристическое уравнение или детерминант возвратной матрицы.

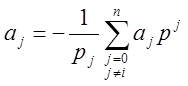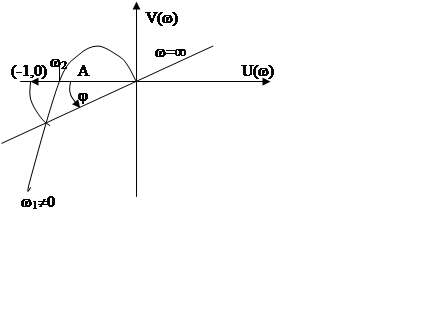
            Условие D(p)=0= - является функциональной зависимостью фиксирующей какое-то распределение корней и параметров. Если взять и указанную неявную зависимость сделать явной относительно любого параметра , то зависимость будет при р=jw представлять преобразование пространства a+jb в U(w)+jV(w)=a_j и в том же числе мнимую ось jw. Пусть преобразование может быть представлено как на рисунке, т.е. однолистная область преобразована в многолистную. Как правило, областью устойчивости является пересечение областей.