Расчет и проектирование привода ленточного конвейера (мощность на тихоходном валу - 4,6 кВт)

1. Общие расчеты

1.1  Выбор    электродвигателя

При постоянной нагрузке необходимая мощность электродвигателя (Р_{эд треб}) определяется по формуле:

где- мощность на тихоходном валу:

;

- общий КПД привода:

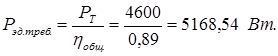
Определяем частоту  вращения выходного вала:

.

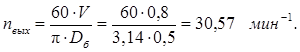Требуемая частота вращения электродвигателя равна:

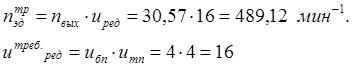
Выбираем электродвигатель типа:

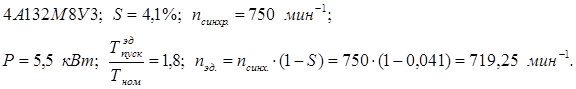
Проверка двигателя на пуск:

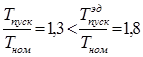
То есть окончательно принимаем электродвигатель

1.2  Разбивка  общего  передаточного  отношения  привода

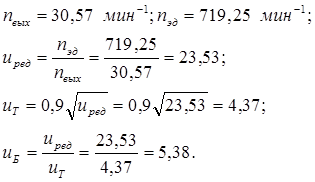
1.3. Определение   крутящего   момента   (Т)   н а   валах

Определяем  со стороны выходного вала:

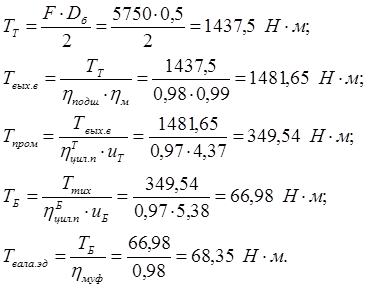
Определим частоты вращения валов:

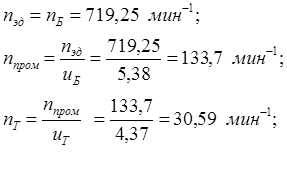
2.  Конструирование и расчет зубчатых передач

2.1.  Тихоходная  ступень

Общее время работы привода

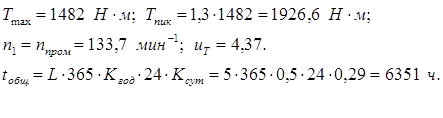
Материалы:        Шестерня  - 40ХН:

Термообработка- закалка ТВЧ

D = 200 мм;     S = 125 мм;

                                 твердость  269 – 302  HB; 48 – 53 HRC                                      

Колесо  -  40ХH:

Термообработка- улучшение

D = 315 мм;     S = 200 мм;

твердость  235 – 262  HB;

Предварительное межосевое расстояние:

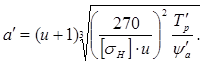
Расчетный момент:  

Коэффициент долговечности: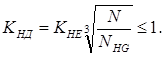  

Т.к. материалы колеса и шестерни одинаковы, а твердость шестерни выше, то лимитирует колесо.

Наработка колеса: 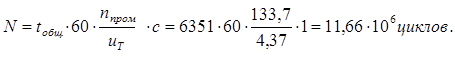 , где С=1- число вхождений в зацепление зубьев зубчатого колеса за один его оборот

База контактных напряжений по [3, стр. 82, табл. 4.6.] при HВ = 248 принимаем

Коэффициент эквивалентности:

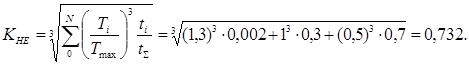
Следовательно, коэффициент долговечности

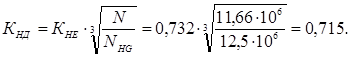
Коэффициент нагрузки по формуле: 

Предварительное значение окружной скорости: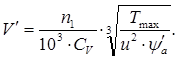 

Коэффициент ширины выбираем по [3, стр. 53, табл. 3.3.] .

Коэффициент  по  [3, стр. 95, табл. 4.9.].

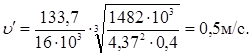
Степень точности – 9 по  [3, стр. 96, табл. 4.10.].

Коэффициент распределения нагрузки по [3, стр. 92, рис. 4.7.] 

Отношение ширины колеса к среднему диаметру шестерни:

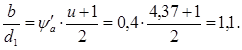
Коэффициент концентрации: 

Начальный  коэффициент  концентрации для  схемы  5  по  [3, стр. 94, рис. 4.8.]   

Коэффициент режима определяем по формуле:

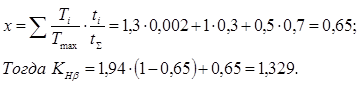
Коэффициент динамичности по [3, стр. 96, табл. 4.11.]

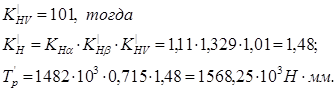
Допускаемое контактное напряжение по [3, стр. 90, табл. 4.6.]

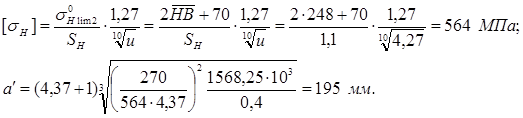
В соответствие с единым рядом главных параметров  [3, стр. 51.] принимаем ближайшее стандартное  значение  Принятое межосевое расстояние больше необходимого и 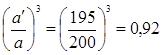, то коэффициент ширины не изменяем.

Ширина колеса .

Действительная скорость определяется по формуле:

Так как , то коэффициенты не уточняем.

Фактическое контактное напряжение

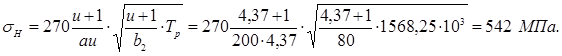
Разница между фактическим и допускаемым напряжениями

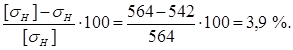
Результат следует считать хорошим.

Наибольшее допускаемое контактное напряжение  по[3, стр. 90, табл. 4.6.]:

Максимальное контактное напряжение по формуле:

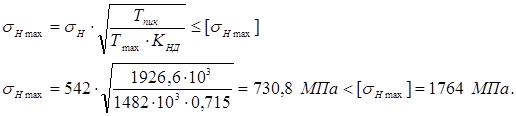
Окружная сила

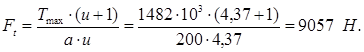
Модуль по формуле: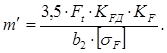    

Коэффициент долговечности по изгибу: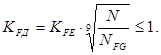

Коэффициент эквивалентности по изгибу по [3, стр. 90, табл. 4.1.]: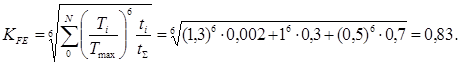

База изгибных напряжений

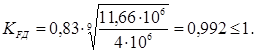
Коэффициент нагрузки

Коэффициент распределения нагрузки [3, стр. 92]

Коэффициент режима равен:  

Начальный коэффициент концентрации по [3, стр. 94,табл. 4.8.]  для

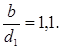
Тогда

Коэффициент динамичности по [3, стр. 97, табл. 4.12.] для ,

Следовательно

Допускаемое напряжение по [3, стр. 90, табл. 4.6.]:

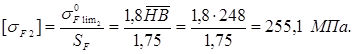
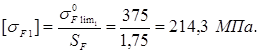
Ширина шестерни по формуле:

Тогда 

Принимаем стандартный модуль равный ближайшему допустимому значению, т.е.

Угол подъема линии зуба определяем по формуле:

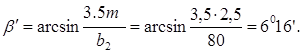
Суммарное число зубьев по формуле:

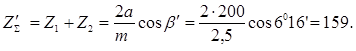
Принимаем

Окончательный угол подъема линии зуба:

Фактический коэффициент осевого перекрытия:

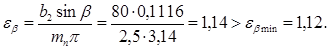
Число зубьев шестерни по формуле:

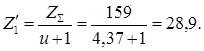
Принимаем

Число зубьев колеса по формуле:

Фактическое передаточное число:

Отклонение фактического передаточного числа от заданного:

Проверяем фактическое напряжение изгиба зубьев шестерни по формуле:

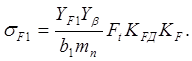
Приведенное число зубьев по формуле:

Коэффициент формы зуба [3, стр. 101, табл. 4.13.]

Коэффициент наклона зуба по формуле:

Таким образом:

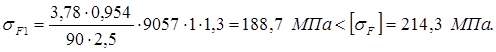
Проверяем фактическое напряжение изгиба зубьев колеса по формуле:

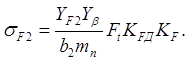
Приведенное число зубьев по формуле:

Коэффициент формы зуба [3, стр. 101, табл. 4.13.]

Таким образом:

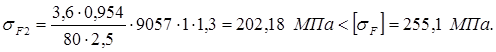
Как видно, фактические изгибные напряжения не превышают допускаемых, значит нам удалось обеспечить изгибную равнопрочность шестерни и колеса.

Наибольшее допускаемое напряжение на изгиб по [3, стр. 90, табл. 4.6.]

Максимальное напряжение изгиба определяем по формуле:

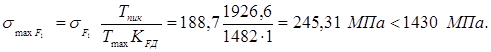
Максимальное напряжение изгиба определяем по формуле:

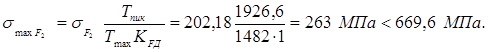
Окончательные параметры передачи:

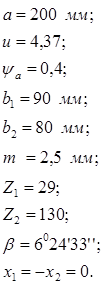
2.3. Геометрический  расчет  цилиндрической  передачи.

Определяем делительные диаметры:

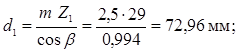
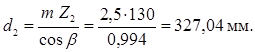
Проверяем условие для делительных диаметров:

Диаметры вершин зубьев находим по формуле:

Диаметры впадин зубьев по формуле:

2.4. Силы  в  зацеплении  цилиндрических  передач.

Окружная сила:

Осевая сила:

Радиальная сила:

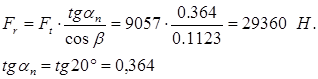
Нормальная сила:

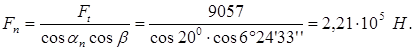
3.  Конструирование и расчет зубчатых передач

2.2. Быстроходная   ступень

Общее время работы привода

часов.

Материалы:     Шестерня  - 40ХН:   

Термическая обработка- улучшение

D = 200 мм;     S = 125 мм;

твердость  269 – 302  HB;

Колесо  -  40ХH:

Термическая обработка- улучшение                       

D = 315 мм;     S = 200 мм;

твердость  235 – 262  HB;

Т.к. редуктор соосный, то межосевые расстояния ступеней равны, т.е.  

Найдём ширину из формулы:

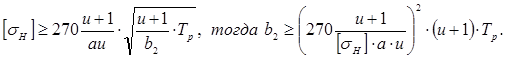
Расчетный момент:

Коэффициент долговечности:

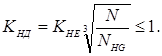
Принимаем твердость шестерни HB₁ = 286, а твердость колеса HB₂ = 262.

Проверяем соотношение твердостей

Так как , то лимитирует шестерня.

Наработка шестерни

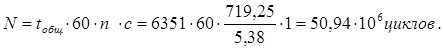
База контактных напряжений по [3, стр. 82, табл. 4.6.] при HВ = 286

Коэффициент эквивалентности:

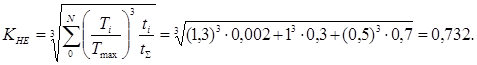
Следовательно, коэффициент долговечности

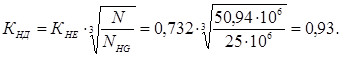
Коэффициент нагрузки по формуле:

Предварительное значение окружной скорости:

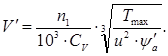
Коэффициент ширины выбираем по [3, стр. 53, табл. 3.3.] .

Коэффициент  по  [3, стр. 95, табл. 4.9.].

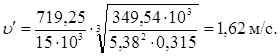
Степень точности – 9 по  [3, стр. 96, табл. 4.10.].

Коэффициент распределения нагрузки по [3, стр. 92, рис. 4.7.] 

Отношение ширины колеса к среднему диаметру шестерни

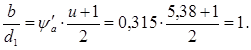
Коэффициент концентрации

Начальный  коэффициент  концентрации для  схемы  5  по [3, стр. 94, рис. 4.8.]   

Коэффициент режима определяем по формуле:

 

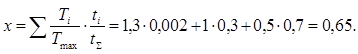
Тогда

Коэффициент динамичности по [3, стр. 96, табл. 4.11.]

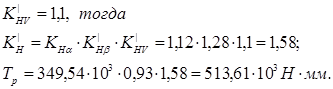
Допускаемое контактное напряжение по [3, стр. 90, табл. 4.6.]

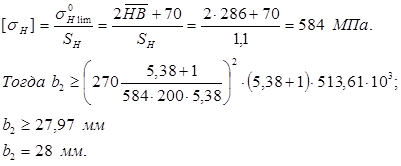
Действительная скорость определяется по формуле:

Объяснить такое расхождение значений  можно тем, что межосевое расстояние мы приняли не расчетное.

Фактическое контактное напряжение

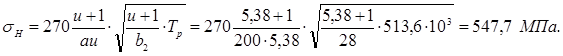
Разница между фактическим и допускаемым напряжениями

 

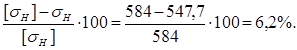
Результат следует считать хорошим.

Наибольшее допускаемое контактное напряжение  по [3, стр. 90, табл. 4.6.]:

Максимальное контактное напряжение по формуле:

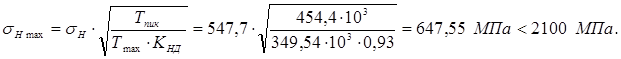
   Окружная сила

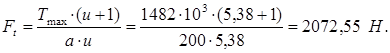
Модуль по формуле: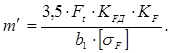    

Коэффициент долговечности по изгибу:

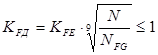
Коэффициент нагрузки

Коэффициент распределения нагрузки

Начальный коэффициент концентрации по [3, стр.94, табл.4.8.]  для

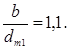
Коэффициент концентрации

Коэффициент динамичности по [3, стр. 97, табл. 4.12.] для , 

Следовательно .

Допускаемое напряжение по [3, стр. 90, табл. 4.6.]:

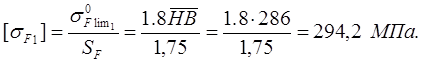
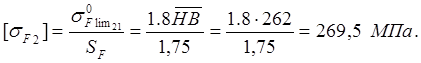
Ширина шестерни по формуле:

Тогда 

Принимаем стандартный ближайший допустимый модуль [3, стр. 53.]

Угол подъема линии зуба определяем по формуле:

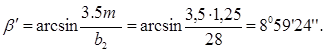
Суммарное число зубьев по формуле:

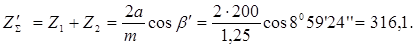
Принимаем

Окончательный угол подъема линии зуба:

Фактический коэффициент осевого перекрытия:

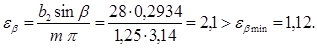
Число зубьев шестерни по формуле:

Принимаем

Число зубьев колеса по формуле:

Фактическое передаточное число:

Отклонение фактического передаточного числа от заданного:

Проверяем фактическое напряжение изгиба зубьев шестерни по формуле:

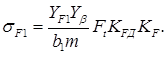
Приведенное число зубьев по формуле:

Коэффициент формы зуба [3, стр. 101, табл. 4.13.]

Коэффициент наклона зуба по формуле:

Таким образом:

Проверяем фактическое напряжение изгиба зубьев колеса по формуле:

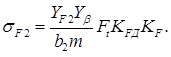
Приведенное число зубьев по формуле:

Коэффициент формы зуба [3, стр. 101, табл. 4.13.]

Таким образом:

Как видно, фактические изгибные напряжения не превышают допускаемых, значит, нам удалось обеспечить изгибную равнопрочность шестерни и колеса.

Наибольшее допускаемое напряжение на изгиб по [3, стр. 90, табл. 4.6.]

Максимальное напряжение изгиба определяем по формуле:

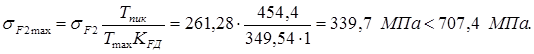
Окончательные параметры передачи:

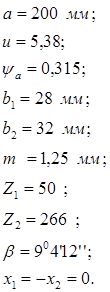
2.3. Геометрический  расчет  цилиндрической  передачи.

Определяем делительные диаметры:

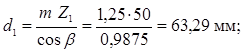
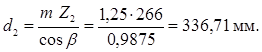
Проверяем условие для делительных диаметров:

Диаметры вершин зубьев находим по формуле:

Диаметры впадин зубьев по формуле:

2.4. С илы  в  зацеплении  цилиндрических  передач.

Окружная сила:

Осевая сила:

Радиальная сила:

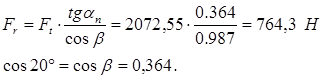
Нормальная сила:

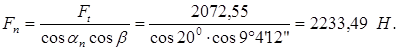
3.3. Б ы с т р о х о д н ы й   в а л

3.3.1. Проектный расчет вала

Предварительное значение диаметра участков вала для установки подшипников качения определяем по формуле:

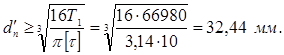
где  для быстроходного вала двухступенчатого соосного редуктора при большом передаточным числе ступени; принимаем

3.3.2. Расчет шпоночных соединений

3.3.2.1. Соединение вала с муфтой

Вращающий момент передается обыкновенной призматической шпонкой с одним  плоским и другим закругленным торцем. Осевое фиксирование полумуфты осуществляется установочным винтом, который стопорится от самоотвинчивания пружинным замковым кольцом.

Для  вибираем по табл.2.2 [4, c.4]  и  длину конца вала по исп. 2:            l = 58 мм. По диаметру вала вибираем обыкновенную  призматическую шпонку шириной         b = 10 мм, высотой h = 8 мм, длиной l = 50 мм, с глубиной паза вала t₁ = 5 мм.    

Рабочая длина шпонки:

l_р = l – 0,5*b= 50 – 0,5*10 = 45 мм.

Номинальное давление на поверхности контактабоковойгранишпонки с пазом ступицы полумуфты по формуле 2.1 [5, c.6]

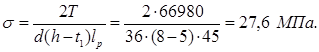
Допускаемые давления в неподвижном соединениисо стандартной шпонкой при переходной посадке чугунной ступицы на стальной вал из табл.2.1 [5, c.6]

Условие износостойкости шпоночногосоединения

выполняется.

Условие прочности на смятие шпоночногосоединения

выполняется.

3.3.3. Конструирование вала-шестерни

Размеры цилиндрического конца вала из расчета шпоночных соединений: диаметр  длина  высота заплечика  Длина шпоночного паза  принимаем стандартную длину [3,с.302]

принимаем диаметр под манжетное уплотнение [3,с.357]

Предварительно выбираем [3,с.531] радиальные однорядные шарикоподшипники тяжелой серии 409, у которых размер фаски:  Наименьшая высота заплечика для упора подшипника [2, с.90] при размере фаски  равна . Требуемый диаметр ступени вала для упора подшипника , принимаем