Динамический анализ механизма вытяжного пресса

3. ДИНАМИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА вытяжного пресса.

Динамический синтез механизма проводим с целью снижения колебаний величины угловой скорости начального звена, вследствие постоянного изменения нагрузок и неравномерности движения. Для снижения колебания угловой скорости начального звена до допустимых пределов в машине предусматривают маховик, который с целью уменьшения его размеров устанавливают на быстроходном валу.

При определении момента инерции маховика I_м вместо реального механизма рассматривают его одномассовую динамическую модель. Динамическая модель механизма состоит из  начального  звена, к которому приведены силы и моменты, движущие М_пд и сопротивления М_пс, действующие на звенья машины, и моменты инерции звеньев I_n . Начальное звено называется звеном приведения.

3.1. Определение параметров динамической модели.

Для построения динамической модели механизма  в качестве звена приведения выбираем начальное звено 1, к которому приводим все силы, действующие на механизм и моменты инерции подвижных звеньев.

3.1.1 Находим приведенный момент инерции и его производную

Приведенный момент инерции определяется по формуле, которая имеет следующий вид:

,                                                   (3.1)

где n – число подвижных звеньев, массы и моменты инерции которых заданы; m_i – масса -го звена; I_Si – момент инерции -го звена относительно оси, проходящей через центр масс; ,  - проекции на оси координат аналога скорости центра масс -го звена;  – аналог угловой скорости -го звена.

Для данного механизма, с учётом того что масса 4-го звена не указана, формула (3.1) принимает вид:

           (3.2)

  где  – аналог угловой скорости ротора двигателя.

Дифференцируя по обобщенной координате  выражение (3.2), находим производную приведенного момента инерции:

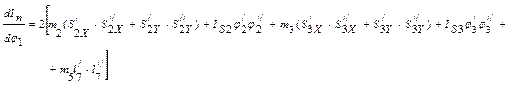                (3.3)

 

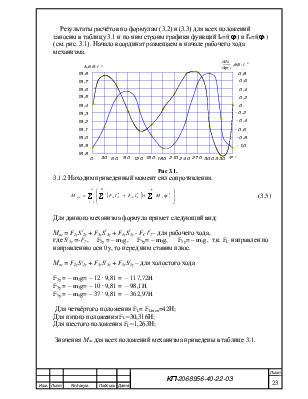
Результаты расчётов по формулам (3.2) и (3.3) для всех положений заносим в таблицу 3.1 и по ним строим графики функций I_n=f(j₁) и I^/_n=f(j₁) (см. рис. 3.1). Начало координат размещаем в начале рабочего хода механизма.

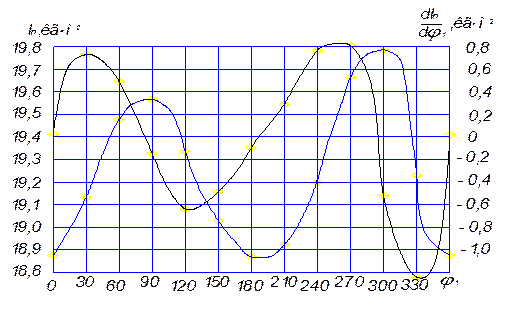
Рис 3.1.

3.1.2 Находим приведенный момент сил сопротивления.

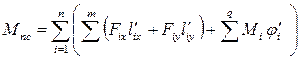                                                 (3.5)

Для данного механизма формула примет следующий вид:

М_пс = F_2yS^/_2y + F_3yS^/_3y + F_5yS^/_5y - F_C l^/₇– для рабочего хода,

где S^/_5y =- l^/₇,     F_2y = – m₂g,     F_3y= – m₃g,      F_5y= – m₅g,  т.к. F_C направлен по направлению оси 0y, то перед ним ставим плюс.

М_пс = F_2yS^/_2y + F_3yS^/_3y + F_5yS^/_5y – для холостого хода

F_2y = – m₂g= – 12 ^. 9,81 =  – 117,72H

F_3y = – m₃g= – 10 ^. 9,81 =  – 98,1H

F_5y = – m₅g= – 37 ^. 9,81 =  – 362,97H

 Для четвёртого положения F_C= F_Cmax=42Н;

Для пятого положения F_C=30,316Н;

Для шестого положения F_C=1,263Н;

Значения М_пс для всех положений механизма приведены в таблице 3.1.

3.2 Определение приращения кинетической энергии.

Построив динамическую модель исследуемого механизма, приступим к ее анализу. Анализ динамической модели будем проводить с помощью графоаналитического метода Виттенбауэра. Для построения диаграммы необходимо знать законы изменения приведенного момента инерции I_п и приращения кинетической энергии Т. Найдем закон изменения приращения кинетической энергии.

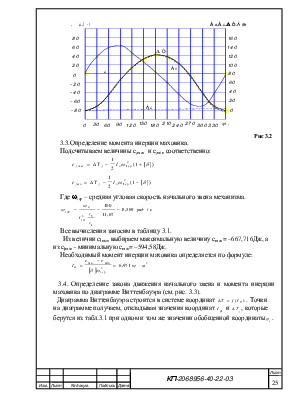
Сначала, в соответствии с (3.5)  и таблицей 3.1 строим график функции     М_пс = f(₁) (см. рис. 3.2). При построении графика М_пс = f(₁) координатную систему располагаем в начале рабочего хода исследуемого механизма. Затем находим работу А_с приведенного момента сил сопротивления М_пс. Работу А_с определяем численным интегрированием функции М_пс=f(₁). Интегрирование проводим, используя метод трапеций, в соответствии с которым

A_c(j+1)=A_cj+(M_пс(j+1)+М_{пс j})(j_1(j+1) - j_1j)/2                                                        (3.6)

j=1,2…- номера положения механизма. Для начального положения А_с1=0. Значения углов j_1j подставляем в радианах.

Значения А_с, найденные по формуле (3.6), заносим в таблицу 3.1 и по ним строим график функции А_с=f(j₁) (см. рис. 3.2).

  В установившемся режиме работа А_с приведенного момента сил cопро-тивления за цикл равна работе приведенных движущих сил А_ПД. Считая, что привод развивает постоянный по величине приведенный момeнт движущих сил М_ПД, найдем его величину:

Строим график функции М_ПД=f(j₁) (см. рис. 3.2).

Работу А_Д приведенного момента движущих сил М_ПД вычисляем по формуле:

Где  =1,2…- номер положения механизма, а А_Д1=0 – работа М_ПД в начальном положении.

Рассчитанные по формуле (3.7) значения работы движущих сил заносим в таблицу 3.1 и по ним строим график функции А_Д=f(j₁) (см. рис. 3.2).

Находим закон изменения приращения кинетической энергии DT, для чего алгебраически складываем работы А_Д и А_С

 где j =0,1,2…- номер положения механизма. Результаты вычислений заносим в таблицу 3.1 и по ним строим график зависимости DT= f(j₁) (см. рис. 3.2).

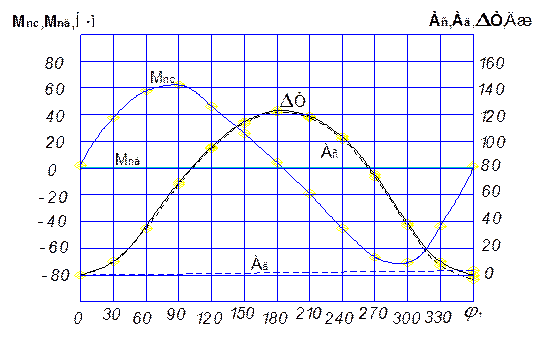Рис 3.2

3.3.Определение момента инерции маховика.

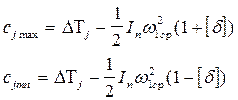Подсчитываем величины с_jmax  и с_jmin соответственно:

Где w_1ср – средняя угловая скорость начального звена механизма.

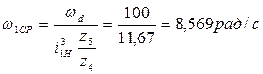
Все вычисления заносим в таблицу 3.1.

      Из величин с_jmax выбираем максимальную величину с_max= –667,716Дж, а

из с_jmin - минимальную с_min= –594,58Дж.

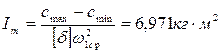Необходимый момент инерции маховика определяется по формуле:

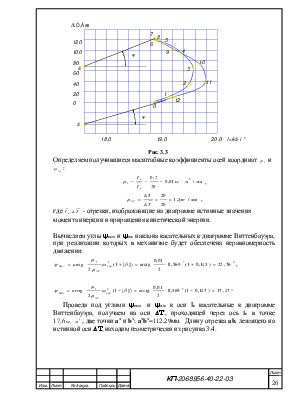
3.4. Определение закона движения начального звена и момента инерции маховика по диаграмме Виттенбауэра (см. рис. 3.3).

  Диаграмма Виттенбауэра строится в системе координат . Точки на диаграмме получаем, откладывая значения координат  и , которые берутся из табл.3.1 при одном и том же значении обобщенной координаты.

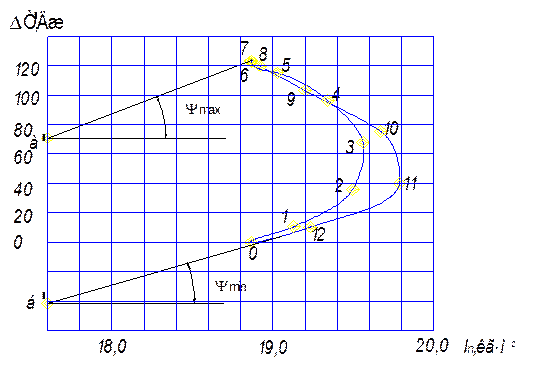
Рис. 3.3

Определяем получившиеся масштабные коэффициенты осей координат