Анализ рычажного механизма, состоящего из семи одноподвижных кинематических пар

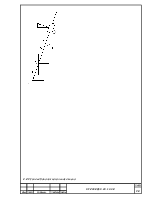
Через конец вектора V_b1 проводим прямую параллельную СВ, это будет направление V_b3/b1  .

С другой стороны точка b участвует во вращательном движении звена 3 относительно точки С.

V_b3 = V_b3/С2

Из полюса плана скоростей – р перпендикулярно СВ, до пересечения с направлением V_b3/в1 строим направление V_b3. Точка пересечения построенных направлений (т. b3) определит отрезки b1b3 = 38 мм аналог V_b3/b1 = b3b1×m_v = 0.076 м/с, и pb3=32,8мм – аналог V_b3/c = pb3×m_v = 0,065 м/с.

Зная линейную скорость определим угловую:

w3 = V_b3/c / l3 = 0.065 / 0,305 = 0.215 c^-1

Полученные значения заносим в табл. 2,4

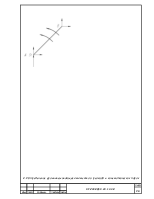
5.  Определяем скорость точки D.

 , тогда

Скорость точки D раскладываем на две составляющие вертикальную и горизонтльную. Вертикальная составляющая V_d будет скоростью точки S₅.

определим горизонтальную составляющую

Заносим полученные данные в табл 2.4

По теореме подобия найдем координаты скоростей центров масс.

V_S5 =Ve верт = 0,016 м/с

Откладываем точку S₃ на плане скоростей.

 , тогда 9.88 мм

рs₃ – аналог скорости центра масс звена 3. В проекциях на оси координат.

ps3x = 9,3мм,    s_3x = m_v×ps2x = 0,018 м/с

ps3y = 3,2мм,    s_3y = m_v×ps2y = 0.006 м/с

2.4. Определение ускорений звеньев механизма

2.4.2.  Аналитический метод

Ускорение звеньев механизма аналитическим методом находим дифференцированием выражений скоростей (2,6), (2,7), (2,8) и (2,9) по обобщенной координате j1.

Дифференцируем систему (2,6)

Решая, эту систему относительно неизвестных:

В расчетном положении получим следующие значения:

j₂¢¢=-0,139L₂¢¢=-0,052. м                        Заносим в таблицу 2.6.

Дифференцируем уравнение (2,7)

Решаем относительно неизвестных:

Врасчетном положении:l₄¢¢ = -0.08

Дифференцируем (2,8), (2,9)

Врасчетном  положении:

S_3x¢¢ = -0.012, мS_3y¢¢ = 0.009, мS₅¢¢ = 0.022, м

Значения ускорений в остальных положениях рассчитаны в MathCAD и занесены в таблицу 2.7.

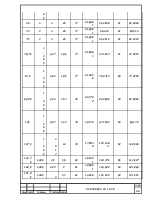
Таблица 2.6

Погрешность - в пределах допустимой. Расчет считаем верным.

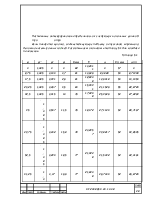
Результаты расчёта аналогов ускорений

Таблица 2,7.

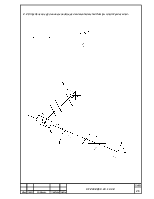
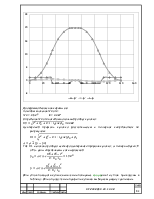
2.4.2.  Определение аналогов ускорений исследуемого механизма графическим методом.

Задачу решаем путем построения плана ускорений, считая ω постоянной величиной.

1.  Определение ускорения точки B₁

Полное ускорение точки B равно нормальной составляющей , которая направлена по AB к центру B.

=0.1

2.  Из точки p – полоса плана ускорений – откладываем вектор, изображающий ускорение точки B в виде отрезка pa=100мм

3.  Масштабный коэффициент: m_а=/Ра = 0,1/100 = 0,001 (м/с²)/мм

4.  Для определения ускорения точки В записываем два векторных уравнения, рассматривая движение этой точки в начале со первым звеном, а затем с третьим:

Нормальные ускорения параллельны звеньям, касательные - перпендикулярные.

Нормальные ускорения вычисляем:

= 0,0132  м/с²

Отрезок, изображающий в мм вектор этого ускорения:

 = 13,2 мм. Вектор  - направлен вдоль ВС от В к С.

Кориолисово ускорение:

=2ω₃ v_B3B1= 0,052 м/с², вектор изображающий  - b₁k= 0,052  μ_а =52    мм. направление определим поворотом скорости v_B3B1 на 90° по направлению w1.

Через n₂ и к проводим направления вектора касательного ускорения, пересечение которых определяет точку b₃.

πb3 = 45,7 мм,  = 0,0457 м/с² _.

πn₁ = 13.2 мм,  = 0,0132м/с² _.

n₁b₃ = 43.7 мм,  = 0,0437м/с² _.

 = 0,0437/0,305 = 0,143 с^-2`

Ускорение центра масс звена3:

По методу подобия.т.о. получаем точку S₃ – конец вектора ускорения центра масс звена 3.

ps3x = 12,                              a_s3x = m_a×ps3x = 0.012 м/с

ps3y = 9 мм,                         a_s3y = m_a×ps3y = 0,009 м/с

По методу подобия.т.о. получаем точку d.Раскладываем πd на горизонтальную и вертикальную составляющие, вертикальная составляющая и будет вектором ускорения точкиS₅, а горизонтальная составляющая -L₄¢¢:

ps5y = 23,3мм,                     a_s5y = m_a×ps5y = 0.0233 м/с²

ps = 30,4мм,                         a_s5y = m_a×ps5y = 0.0304 м/с²

3  ДИНАМИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА.

Внутри цикла установившегося движения угловая скорость начального звена машины периодически меняется из-за постоянного изменения нагрузок, что приводит к нежелательной неравномерности движения. Неравномерность движения начального звена характеризуется коэффициентом неравномерности движения [d]. При анализе динамики машины и определении момента инерции маховика I_м вместо реального механизма рассматривают его одномассовую динамическую модель. Динамическая модель механизма состоит из одного, начального звена. К которому приведены силы, движущие моменты М_пд и моменты сопротивления М_пс, действующие на звенья машины, а также все моменты инерции звеньев  Iп. Для определении требуемого значения момента инерции маховика Iм запишем уравнения движения звена приведения в форме интеграла энергии для промежутков времени, за которое его угловая сорость изменится от ω0 до ωmax и от ω0 до ωmin

Вычтем из первого второе и учитывая что:

Получим:

Iм = (Сmax–Cmin)/ [d]×w²_cp

3.1  Определение параметров динамической модели.

Для построения динамической модели исследуемой машины в качестве звена приведения выбираем звено 1, к которому приводим все силы (моменты), действующие на механизм и моменты инерции подвижных звеньев.

3.1.1 Приведенный момент инерции и его производная.

Приведенный момент инерции определяется по формуле.

Где n  - число подвижных звеньев, массы и моменты инерции которых заданы;

mi  - масса i –го звена; Six¢ и Siy¢- проекции на оси координат аналога скорости i –го звена; Ii – момент инерции i –го звена; ji¢- аналог угловой скорости

i –го звена;

Для рассматриваемого механизма в расчетном положении

In =I_d (j_d¢)² + I_s3 + I_s3 (j₂¢)² + m₃×((S_3x¢)² + (S_3y¢)²) + m₅ (L₅¢)²

jd¢ = i3н ×(Z5/Z4) = 10.2 - аналог угловой скорости ротора двигателя.

В расчетном положении: In = 1.239 кг м²

Дифференцируя по обобщенной координате j1, находим производную приведенного момента инерции

d In /dj1 = 2[Is3 j2¢j2¢¢+ m5 L5¢L5¢¢+ m3 (S3x¢S3x¢¢ +S3y¢S3y]

В расчетном положении: dIn/dj1=-0.058 кг×м².

Для остальных положений механизма In и dIn/dj1 рассчитаны