Саратовский Государственный технический университет
Кафедра «Техническая кибернетика и информатика»
Расчетно-графическая работа
по дисциплине
«Программирование и основы алгоритмизации»
на тему:
АЛГОРИТМЫ ГЕНЕРАЦИИ ПСЕВДОСЛУЧАЙНЫХ
ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Выполнил: Студент группы сзУИТ-11
Радионова Ю.Е.
Проверил:
доц. Гуреев В.В.
Саратов 2011 г.
Содержание
1) Введение………………………………………………………………………3
2) Класс CRandom, содержащий: ………………………………………….4
a) параметры линейного конгруэнтного генератора (a, c, m);
b) функцию SetRandom (), позволяющую инициализировать (устанавливать в исходное состояние) генератор;
с) функцию longGetRandom (), возвращающую значение (одно) псевдослучайной последовательности;
c) функцию GetRandom (long* arr, N), возвращающую псевдослучайную последовательность (массив) длиной N;
3) Функция для реализации линейного конгруэнтного генератора последовательности псевдослучайных чисел…………………………5
4) Функция для реализации генератора Парка и Миллера…………… ..6
5) Функция для реализации генератора Парка и Миллера с перемешиванием……………………………………………………………7
7) Литература…………….………………………………………………….....9
8)Приложение 1. Графики для линейной конгруэнтной последовательности
9)Приложение 2. Графики для генератора Парка и Миллера.
10)Приложение 3. Графики для генератора Парка и Миллера с перемешиванием.
11) Приложение 4. Графики для генератора с большим периодом.
Введение
При проведении компьютерного моделирования некоторых объектов могут потребоваться случайные последовательности. Поскольку все алгоритмы, реализуемые на ЭВМ, являются полностью детерминированными, то и последовательность чисел, получаемая с помощью данных алгоритмов, не может быть полностью случайной. Такие последовательности относятся к классу псевдослучайных последовательностей. Псевдослучайные последовательности отличаются от полностью случайных тем, что имеют период повторения, как правильно достаточно большой.
Большинство реализаций языка С содержат в своей библиотеке стандартные процедуры инициализации и генерации псевдослучайных чисел. Например:
#include <stdlib.h>
#define RAND_MAX ...
void srand(unsigned seed);
intrand(void);
Процедура srand(seed) служит для инициализации (задания начальной точки) псевдослучайной последовательности путем передачи произвольного числа seed. Одинаковые значения seed всегда будут инициализировать одинаковые псевдослучайные последовательности. Для получения последовательных значений псевдослучайной последовательности необходимо вызывать функцию rand() столько раз, сколько значений нужно получить. Функция rand() возвращает целое число, находящееся в диапазоне от 0 до RAND_MAX. Если требуется получить вещественное число x в диапазоне [0,1), то необходимо произвести нормировку
x = rand()/(RAND_MAX+1.0);
Функция SetRandom () – устанавливает в исходное состояние генератор:
int* SetRandom()
{
int F = 1;
int *X = &F;
return (X);
}
Функция longGetRandom () - возвращает значение
псевдослучайной последовательности:
long GetRandom(int &X, long a, long c, long m)
{
int Xn = ((a*(X)+c)%m);
X = Xn;
return Xn;
}
Функция GetRandom (long* arr, N) - возвращает псевдослучайную последовательность длиной N:
long* GetRandomarr(long *arr,int N,long a, long c, long m)
{
int X = 1;
for(int i=0;i<N;i++)
{
arr[i]=(a*X+c)%m;
X = arr[i];
}
return arr;
}
Функция для реализации линейного конгруэнтного генератора последовательности псевдослучайных чисел.
Почти все библиотечные генераторы rand() используют линейное конгруэнтное преобразование:
Xn+1 = (aXn + c) mod m,
где a – множитель, c – инкремент, m – модуль. z mod y означает остаток от целочисленного деления [z/y]. Период последовательности (1) не превышает m, а значения Xn находятся в диапазоне от 0 до m-1. Период последовательности зависит от выбора параметров (a, c, m). Наиболее качественными генераторами считаются те, у которых период максимален (близок к m-1).
Параметры: a=1093, c=18257, m=86436;
long GetRandom(int &X, long a, long c, long m)
{
int Xn = ((a*(X)+c)%m);
X = Xn;
return Xn;
}
Функция для реализации генератора Парка и Миллера
Парк и Миллер предложили генератор, у которого
a = 75 = 16807, m = 231 – 1 = 2147483647 (3)
Существует преобразование (преобразование Шрейджа), которое позволяет осуществлять перемножение 32-битных целых чисел по модулю 32-битной константы. Согласно данному преобразованию модуль m
представляют как
m = aq+ r, где q = [m/a], r = m mod a (4)
Если r < q и 0 < z < m – 1, то можно показать, что и a(z mod q), и r[z/q]
находятся в диапазоне от 0 до m – 1, и
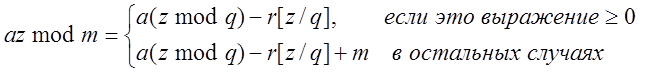
Для констант (3) преобразование Шрейджа использует параметры
q = 127773 и r = 2836.
Другие параметры генератора:
m = 231 – 1, a = 48271 (q = 44488, r = 3399)
m = 231 – 1, a = 69621 (q = 30845, r = 23902)
float ran0(long *idum)
{
long MM = 2147483647;
long k;
static long F = *idum;
float ans;
F ^= MASK;
k=(*idum)/44488;
F=a *(F-k*q)-r*k;
if(*idum < 0) F += MM;
ans=(1.0/MM)*(F);
F ^= MASK;
return ans;
}
Функция для реализации генератора Парка и Миллера с перемешиванием
Недостатком генератора Парка и Миллера является корреляция между значениями последовательности. Для уменьшения корреляции используется алгоритм перемешивания, который заключается в следующем. Случайное число iy определяет индекс элемента массива случайных чисел из 32 элементов (iy должно нормироваться к диапазону 0...31). Элемент с данным индексом содержит выходное значение последовательности, которым также инициализируется iy. В данный элемент массива записывается новое значение, генерируемое с помощью генератора Парка и Миллера.
Длина последовательности ~ 108.
float ran1(long *idum)
{
static long F = *idum;
int j=0;
long k=0;
static long iy=0;
static long iv[32];
float temp;
if (F <= 0 || !iy) {
if (-(F) < 1) F=1;
else F = -(F);
for (j=NTAB+7;j>=0;j--) {
k=(F)/IQ;
F=IA*(F-k*IQ)-IR*k;
if (F < 0) F += IM;
if (j < NTAB) iv[j] = F;
}
iy=iv[0];
}
k=(F)/IQ;
F=IA*(F-k*IQ)-IR*k;
if (F < 0) F += IM;
j=iy/NDIV;
iy=iv[j];
iv[j] = F;
if ((temp=AM*iy) > RNMX) return RNMX;
else return temp;
}
Функция для реализации Генерация псевдослучайной последовательности с большим периодом
В некоторых случаях требуется генерация псевдослучайной последовательности с очень большим периодом (> 1010). Одним из эффективных методов получения таких последовательностей является объединение двух различных последовательностей с разными периодами. Идея метода заключается в том, чтобы просто суммировать две последовательности по модулю любого из двух модулей последовательностей. Допустим, что этот модуль равен m.
Данный метод был предложен L’Ecuyer. Период новой последовательности равен наименьшему общему кратному периодов двух последовательностей. Для того чтобы избежать переполнение промежуточной целочисленной переменной в данном методе используют операцию вычитания двух случайных чисел вместо суммирования, а затем, к полученному результату добавляют m – 1, если результат вычитания ≤ 0. Добавление m – 1 означает приведение результата к диапазону 0... m – 1.
Объединение двух последовательностей значительно уменьшает корреляцию, однако алгоритм перемешивания все же рекомендуется.
float ran2(long *idum){
int j;
long k;
static long idum2=123456789;
static long iy=0;
static long iv[NTAB];
float temp;
if (*idum <= 0) {
if (-(*idum) < 1) *idum=1;
else *idum = -(*idum);
idum2=(*idum);
for (j=NTAB+7;j>=0;j--) {
k=(*idum)/IQ1;
*idum=IA1*(*idum-k*IQ1)-k*IR1;
if (*idum < 0) *idum += IM1;
if (j < NTAB) iv[j] = *idum;
}
iy=iv[0];
}
k=(*idum)/IQ1;
*idum=IA1*(*idum-k*IQ1)-k*IR1;
if (*idum < 0) *idum += IM1;
k=idum2/IQ2;
idum2=IA2*(idum2-k*IQ2)-k*IR2;
if (idum2 < 0) idum2 += IM2;
j=iy/NDIV1;
iy=iv[j]-idum2;
iv[j] = *idum;
if (iy < 1) {iy += IMM1;}
if ((temp=AM1*iy) > RNMX) return RNMX; else return temp;
Литература
1. Стенли Б., Жози Лажойе, «Язык программирования С++»
2. Айвор Хортон, «Visual C++», 2005
3. Брюс Эккель, «Философия С++»
4. Справочник советов и примеров по С++Builder
5. В.В. Подбельский, «Язык С++»
6. Н. Вирт, «Алгоритмы и структуры данных»
7. Ален И. Голуб, «Правила программирования на Си и Си++»
8. Харви Дейтел, Пол Дейтел, «как программировать на С++»
9. Богуславский А.А. Основы программирования на языке Си++: Для студентов физико-математических факультетов педагогических институтов / А.А. Богуславский, С.М. Соколов – Коломна: КГПИ, 2002. – 490 с.
10. 6. Рейсдорф К. Borland C++ Builder. Освой самостоятельно / К. Рейсдорф, К. Хендерсон; Пер. с англ. под ред. Т. Москалева – М.: Бином, 1998. – 702 с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.