Анализ и синтез механизмов сенного пресса (Кинематический анализ механизма грохота)

Кинематическое исследование машин и механизмов аналитическим методом.

Для определения кинематических характеристик механизма применим методом замкнутых векторных контуров.

1. Рисуем в любом промежуточном положении структурную схему исследуемого механизма.

2. Выбираем координатную систему. Обычно начало координат связывают со стойкой начального звена.

3. В соответствии с методом все звенья механизма, включая и стойку, заменяют векторами произвольного направления. Положение в пространстве этих векторов характеризуется углами, величина которых определяется мысленным поворотом против хода часовой стрелки, помещенной в их начало, оси Х до направления соответствующего вектора.

4.  Полученные векторы объединяем между собой так, чтобы их последовательность образовывала два замкнутых контура. Причем в каждый контур должно входить не более двух неизвестных величин.

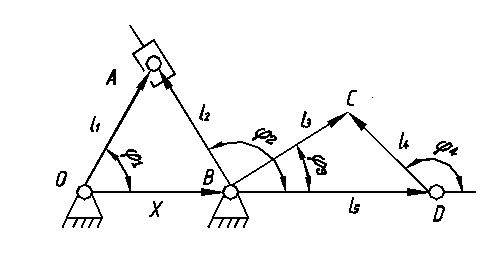
Записываем уравнение замкнутости первого контура в векторной форме. Для этого обходим его периметр, например, в направлении вектора l₁, причем, все векторы совпадающие с направлением обхода, ставятся со знаком «+» и не совпадающие  - со знаком «–»:

                                                                              (2.1)

Уравнению (2.1) соответствуют два уравнения проекций на оси координат:

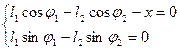      (2.2)

Среди величин, входящих в уравнение (2.2), переменными являются углы  j₁,иj_2,  вектор l2.Угол  j₁ является обобщенной координатой механизма, поэтому он должен быть задан. Из уравнений (2.2) подлежат определению переменные параметры j₂ иl2._.

Из уравнений   (2.2) находим угол наклона вектора l2:        

          (2.3)

и модуль вектора `l₂:

             (2.4)

Уравнение замкнутости второго контура ВСDB имеет вид:

 (2.5) или в проекции на оси координат:

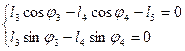.                                         (2.6)

Выражаем j₄  из второго уравнения системы (2.6)

, где     (2.7)

l5  находим из первого уравнения:

     (2.8)

Для определения точек S₃ и S₄ записываем уравнения замкнутости контуров.

(2.9)     

    (2.10) 

Из уравнений (2.9) и (2.10)  находим координаты центров масс звеньев 3 и 4:                                                             

,           (2.11)

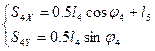                  (2.12)

   (2.13)

 Все вычисленные по формулам величины сравниваем с соответствующими величинами, найденными из плана механизма. Результаты сравнения приведены в табл. 2.2.

Результаты расчета положений звеньев.                                      Таблица 2.2

. Величина	j1°	j2°	j4°	l2, м	l5, м
Графически	217	203.00	170.00	0.381	0.915
Аналитически	216.87	203.20	170.48	0.381	0.915
Отклонение, D %,	0.06	0.1	0.28	0	0

Расчет для остальных 13 положений представлен в таблице 2.8

Определение кинематических свойств механизма, когда закон движения начального звена еще не известен, производится с помощью кинематических характеристик, называемых аналогами скоростей и ускорений, которые не зависят от времени, а являются функциями обобщенной координаты.

Так как аналоги скоростей и ускорений не зависят от закона изменения обобщенной координаты, принимаем w₁ = -1 рад/с.

Аналитическое определение аналогов скоростей основано на дифференцировании по обобщенной координате уравнений (2.2) и (2.6). После дифференцирования уравнений (2.2) получим:

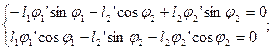    (2.14)       

где j₁’ – аналог угловой скорости звена 1. В расчетах принимаем , так как угловая скорость звена 1 направлена по ходу часовой стрелки; j₂’ – аналог угловой скорости звена 2.

При дифференцировании уравнений (2.6) получаем

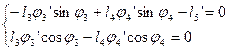                        (2.15)

Выразим из второго уравнения (2.14) l₂’:

                                (2.16)

Подставим во второе уравнение системы (2.14):

      (2.17)

  

           

  Из уравнений (2.15) соответственно находим l₅’, j₄’.

  j₄’ получаем из второго уравнения:                                                                                                 

     (2.18) ,  где      

 

Из первого уравнения системы (2.15) выразим l₅:

           (2.19)

   

                                                                                                                         Аналоги скоростей центров масс звеньев 3, 4 и 5 получаем в проекциях на оси координат, дифференцируя по обобщенной координате уравнения (2.11) и (2.12):

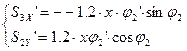(2.20)

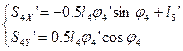  (2.21)                                                                          

                           (2.22)

Аналоги скоростей для 13 положений механизма представлены в таблице         2.8

Аналитическое определение аналогов ускорений основано на дифференцировании по обобщенной координате уравнений (2.14) и (2.15):

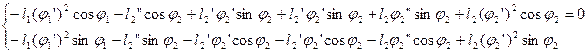 (2.23) 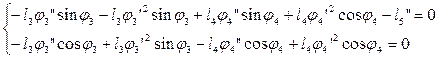                (2.24)

Находим  из (2.23)  и

В первом уравнении системы (2.23) из первого уравнения выразим  , получим:

 (2.25)

подставим  во второе уравнение системы (2.23), получим:

 (2.26)

  

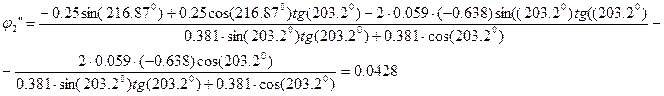
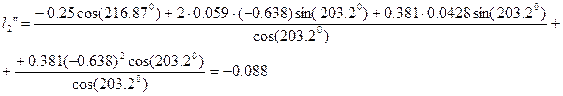
       Из второго уравнения системы (2.24) найдем:

   (2.27)

 

Из первого  уравнения системы (2.24) найдем:

       (2.28)

           

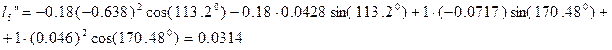
      Дифференцируя по обобщенной координате уравнения (2.20), (2.21)  определяем аналоги ускорений 3, 4  центров масс:

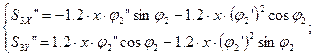     (2.29)

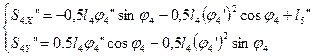     (2.30)

     (2.31)

Результаты расчета аналогов ускорений для всех положений приведены в таблице 2.8.

2.5. Построение планов скоростей и ускорений.

Планом скоростей (ускорений) называют рисунок, на котором в масштабе изображены векторы, равные по модулю и направлению скоростям (ускорениям) различных точек звеньев механизма в данный момент времени. План скоростей (ускорений) механизма, построенный для исследуемого положения механизма, является совокупностью нескольких планов скоростей (ускорений) отдельных точек звеньев, у которых полюса планов являются общей точкой – полюсом плана скоростей (ускорений) механизма.

2.5.1. Определение аналогов скоростей исследуемого станка графическим методом

Решение этой задачи графическим методом основано на построении плана скоростей для третьего положения механизма при . Так как аналоги скоростей и ускорений не зависят от закона изменения обобщенной координаты, принимаем w₁ = 1 рад/с.

План скоростей строим в следующем порядке:

1) находим скорость точки А:

;                                            

2) из полюса плана скоростей р_V – откладываем отрезок перпендикулярный ОА р_Vа1 = 62,5мм, изображающий вектор скорости точки А, принадлежащей 1 звену;

3) подсчитываем масштабный коэффициент плана скоростей:

;

4)  Полное ускорение точки А определяется как :

              (2.32)

Уравнение (2.32) решаем графически. Через точку а1 проводим линию, параллельную АВ, а из точки р_V перпендикулярную АВ. Точка пересечения этих линий есть точка а3.

5) Скорость точки С направлена по линии перпендикулярной р_Vа3. Для определения скорости точки С используем теорему подобия:

   

6) Скорость точки  D находим путем сложения абсолютной скорости точки