Математическое моделирование тепловых процессов в двигателях внутреннего сгорания: Курс лекций (Эволюция учения о теплообмене в ДВС от Нуссельта до наших дней. Основные показатели эффективности циклов тепловых двигателей), страница 4

.                                                    (1.4)

Скорость рабочего тела в цилиндре ДВС он представил в виде суммы двух составляющих:

                                                         W=C₁c_m+C₂DP.                                               (1.5)                     

В этой формуле первое слагаемое соответствует скорости перемещеия рабочего тела, вызванного движением поршня, а также вихревым движением впускного заряда.  При этом определяющей величиной является средняя скорость c_m поршня. Другой причиной движения рабочего тела в цилиндре является процесс сгорания и поэтому второе слагаемое, характеризуется перепадом давлений , который представляет собой разность между давления в цилиндре при наличии процесса сгорания P и без него P₀. Давление P₀ поршневого сжатия-расширения определяв при работе ДВС в режиме прокрутки или на работающем двигателе при отключенной топливоподаче (в случае дизеля) либо свече зажигания (в случае бензинового ДВС) в исследуемом цилиндре. Очевидно, что давления P и P₀ являются функциями от угла поворота коленчатого вала.

Рассмотрим выражения для чисел Нуссельта  и Рейнольдса          , в которых в качестве характерного размера используется диаметр D цилиндра. Учитывая, что молекулярное число Прандтля постоя (Pr=const), а теплопроводность l и кинематическая вязкость n как для воздуха, так и для продуктов сгорания являются величинами, пропорциональными температуре получаем из (1.4)

.

В случае турбулентного течения обычно показатель степени m=0.8, поэтому

                                                    (1.6)

В 1995 г. Вошни придал a-формуле (1.5) следующий вид

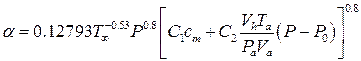.                               (1.7)

Анализ формулы (1.7) указывает на ее эволюцию последние 30 лет. Все изменения, дополнения и уточнения внесенные в эту формулу, были продиктованы развитие ДВС, а также стремлением Вошни и его учеников сделать ее наиболее универсальной. Заметим, что сделали они это достаточно успешно, так как ни одна известная до этот a-формула в целом не позволяет получить такие хорошие приближения к экспериментальным данным, как формул Вошни.

Рассмотрим некоторые особенности формулы (1.7) связанные с ее выводом.

1. В отличие от Нуссельта, который исходил из эксперимента и не смог придать формуле (1.1) обобщенный критериальный вид, Вошни вывел свою формулу при помощи известного критериального выражения с последующим уточнением входящих в нее коэффициентов по данным специально поставленных экспериментов. Исходная концепция Вошни заключалась в том, что течение в цилиндре двигателя уподоблялось стационарному течению в трубопроводе. Диаметр трубопровода заменялся диаметром цилиндра двигателя, средняя скорость потока в трубопроводе - средней скоростью движения поршня, а рабочему телу в ДВС приписывались теплофизические свойства, характерные для газа в трубопроводе. Таким образом, Вошни для расчета нестационарного теплообмена КС использовал теорию подобия.

2. С помощью эмпирических коэффициентов Вошни учитывал сложную взаимосвязь между конвективным и лучистым теплообменом, не выделяя последний в виде от дельной составляющей, как это делали до него Нуссельт, Брилинг, а позднее и Розенблит. Отказ от традиционной аддитивной формы является одним из достоинств, определяющих достоверность формулы Вошни.