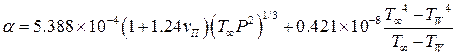 (1.1)
(1.1)
которая имеет аддитивную структуру:
![]() ,
,
где a0 - коэффициент теплоотдачи, соответствующий неподвижному газу в КС, aК - коэффициент теплоотдачи, соответствующий условиям вынужденной конвекции, происходящей со скоростью, пропорциональной средней скорости поршня vП и aR - коэффициент теплоотдачи излучением.
Научный авторитет Нуссельта на многие годы определил развитие работ по теплообмену в двигателях, и поэтому целесообразно остановиться на некоторых обстоятельствах, связанных с началом исследований теплообмена в ДВС. Прежде всего отметим, что размерный вид формулы (1.1) сужает возможности ее экстраполяции на условия опытов, отличных от проведенных Нуссельтом.
Работе Нуссельта предшествовали публикации А. Шака (1924), в которых содержалась резкая критика метода подобия. Так, по мнению Шака, результаты теории подобия нельзя экстраполировать на прикладные задачи, поскольку в реальных устройствах разность температур стенки КС и окружающего цилиндр воздуха заметно отличается от нуля, а коэффициент теплоотдачи равен пределу:
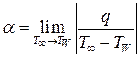 .
.
Все известные задачи теории подобия относились к равномерному или плавно изменяющемуся движению жидкости (течение в трубе, на начальном участке канала и в пограничном слое на пластинке). В этот период создаются инженерные методы расчета неравномерных потоков. Заметим, что движение жидкости неравномерное, если эпюры скорости для различных живых сечений потока в данный момент времени имеют различный вид.
Можно утверждать, что к 1923 г. методы решении задач механики неравномерных потоков были широко известны и, в основном, опубликованы. Нуссельт и Шак не могли не знать об этом, поэтому опубликование формулы (1.1) бесспорно является уступкой Нуссельта оппонентам, причем не оправданной дальнейшим развитием теории теплообмена и механики жидкости. В известной степени аддитивная структура формулы (1.1) также не соответствует современным представлениям теории сложного теплообмена. Нуссельт понимал всю сложность решаемой им задачи, поскольку именно ему принадлежит приоритет введения угловых коэффициентов излучения. Таким образом, не имея достаточных экспериментальных результатов, Нуссельт предложил формально аддитивный подход к описанию сложного (радиационно-конвективного) теплообмена. При этом он был абсолютно точен как исследователь, поскольку в его опытах доля радиации не превышала нескольких процентов интегрального теплового потока. Дальнейшие исследования Нуссельта не првели к существенному прогрессу в области теплообмена в ДВС.
Последователем Нуссельта в этом направлении являлся Н.Р. Брилинг (1876-1961) - профессор МВТУ Баумана. Проводя опыты в 1931 г. по определению теплопотерь в цилиндре малооборотного компрессорного дизеля (n= 200 об/мин), он обнаружил, что интенсивное вихреобразование, обусловленное пневматическим распылом топлива, увеличивает коэффициент теплоотдачи в 2.45 раза. Формула Брилинга имеет вид:
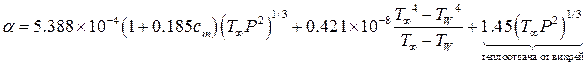 , которая
по структуре может быть представлена в виде
, которая
по структуре может быть представлена в виде
![]() ,
(1.2)
,
(1.2)
где aw- коэффициент теплоотдачи, соответствующий тепплоотдаче от вихрей. Брилинг указывал, что «в быстроходных дизелях теплообмен следует тому же закону, какой был нами найден для стационарного двигателя Дизеля, с той лишь разницей, что в теплопередаче отсутствует постоянный член, выражающий тепло от вихревых движений, вызванных искусственно в процессе распыления топлива». Поэтому при расчетах быстроходных дизелей бескомпрессорного типа принимают aw=0. Заслуга Брилинга очевидна: сохранив структуру формулы (1.1), он доказал, что в каждом конкретном случае (в зависимости от способа смесеобразования, быстроходности, мощности) коэффициенты необходимо уточнять по результатам экспериментов. Этот вывод нашел развитие в работах Н.Н. Брызгова, Ван Тиена, Н.В. Иноземцева, содержащих конкретные выражения для a0, aК; aR и aw для отдельных типов двигателей.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.