Исследование гидросистемы при помощи средств автоматизированного проектирования

Операции и процедуры функционального проектирования, как правило, почти полностью поддаются формализации, что в конечном итоге создает необходимые условия для определения и выбора оптимальных параметров и структуры технического объекта. При этом используются математические модели создаваемых объектов, модели оценки и принятия решений, которые в виде соответствующих алгоритмов реализуются при проектировании.

При решении задач синтеза структуры, моделировании процессов функционирования объектов с переменной структурой возникает необходимость постоянного изменения математической модели. Поэтому большое внимание уделяется методам автоматизированного формирования математических моделей.

На различных этапах и стадиях проектирования сложной технической системы используются различные математические модели. На ранних стадиях обычно модели простые, но чем подробнее проработка проекта, тем сложнее нужна модель. Математические модели могут представлять собой системы дифференциальных уравнений (обыкновенных или в частных производных), системы алгебраических уравнений, простые алгебраические выражения, бинарные отношения, матрицы и др. Сложные модели требуют больших затрат времени на проведение вычислительных экспериментов. Системы уравнений таких моделей обычно отличаются плохой обусловленностью, что создает проблемы обеспечения устойчивости вычислительного процесса, достижения необходимой точности при приемлемых затратах времени.

Поскольку все проектные работы носят оптимизационный характер, то решать системы уравнений для получения искомого результата приходится многократно. Ситуация усугубляется также многомерностью и многокритериальностью задач. На заключительных этапах проектирования часто приходится использовать вероятностные модели, с тем чтобы исследовать процессы функционирования технической системы в условиях, максимально приближенных к реальным.

Если САПР потребует слишком больших затрат времени на разработку проекта изделия, то она вряд ли получит широкое практическое применение.

Отмеченные факторы указывают на необходимость поиска способов ускорения обработки информации и применения эффективных технологических маршрутов выполнения проектных работ. Глубокое знание этих вопросов и умение выбрать правильное решение при создании САПР может принести значительный эффект в сокращении материальных и временных затрат на проектирование. [1]

3. РАССМОТРЕНИЕ ИНДИВИДУАЛЬНОГО ЗАДАНИЯ

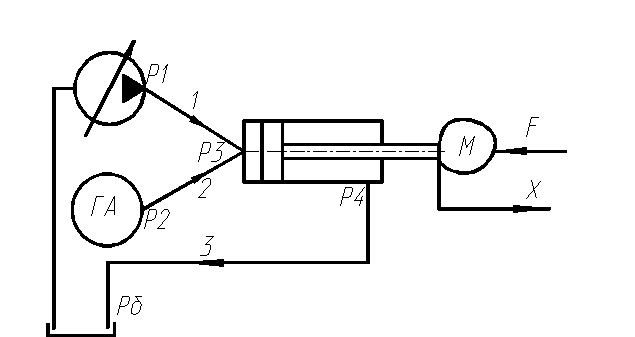
Принципиальная гидравлическая схема привода

Задание на курсовую работу включает принципиальную гидросхему привода, показанную на рисунке. Исполнительным органном является гидроцилиндр, к штоку которого приложена нагрузка по ходу штока, изменения которой показаны на рисунке ниже. Блоком подготовки и предохранения являются: гидробак, насос, гидроаккумулятор. При поступлении в бесштоковую полость гидроцилиндра рабочей жидкости гидроцилиндр совершает рабочих ход (поршень движется вправо). [1]

Изменение нагрузки по ходу штока

Исходные данные:

Площадь на выпуск штока    Sв = 20 см²;

Площадь на уборку штока     Sу = 18см²;

Длина 1 трубопровода l1 = 1,5 м;

Длина 2 трубопровода l2 = 2,5 м;

Длина 3 трубопровода l3 = 3 м;

Диаметр 1 трубопровода       d1 = 0,0024 м;

Диаметр 2 трубопровода       d2 = 0,0100 м;

Диаметр 3 трубопровода       d3 = 0,0085 м;

Характеристика насоса

Объём воздушной полости гидроаккумулятора V0 = 3,5 л;

Давление зарядки гидроаккумулятора воздухом        Рз =20 МПа;

Кинематическая вязкость жидкости         n = 0,2505×10^-4 м2/с;

Плотность рабочей жидкости r = 890 кг/м³;

Давление в баке  Рб = 1,1 МПа;

Масса, приведенная к штоку   М = 27 кг;

Ускорение свободного падения g = 9,8 м/с².

Нужно провести расчёт переходного процесса выпуска штока гидроцилиндра на полный ход, построить графики давления насоса в полостях гидроцилиндра, хода штока, подачи насоса и гидроаккумулятора.

Исследовать влияние плотности рабочей жидкости на выпуск штока гидроцилиндра на полный ход.

Для проведения расчета используем дифференциальные уравнения:

Уравнение неразрывности потока рабочей жидкости

Qi вх - Qi вых = 0

Дифференциальное уравнение неустановившегося движения несжимаемой жидкости

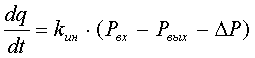, где kин — коэффициент учитывающий инерцию жидкости в трубопроводе;

Рвх, Рвых — соответственно давление на входе в рассматриваемый участок трубопровода и на выходе из него;

DР — суммарные потери давление на рассматриваемом участке.

Дифференциальное уравнение неустановившегося движения штока поршня гидроцилиндра

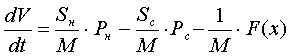, где Sн, Sс — соответственно площадь штока со стороны нагнетательной и сливной полостей;

Рн, Рс — соответственно давления в напорной и сливной полости гидроцилиндра;

М — приведенная к штоку гидроцилиндра масса;

F(x) — активная сила вдоль штока гидроцилиндра.

Дифференциальное уравнение изменения давления в пневмогидроаккумуляторе

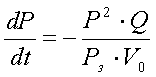, где Рз — давление зарядки пневмогидроаккумулятора;

V0 — объем воздушной полости гидроаккумулятора.

Зависимость между расходом рабочей жидкости протекающей в гидроцилиндре и скоростью движения штока гидроцилиндра:

Q = V × S.

ЗАКЛЮЧЕНИЕ

В результате работы получили зависимости хода штока и расходы во всех