Сопротивление цепи активное, и по отношению к входным зажимам цепь содержит
только активное сопротивление ![]() . При этом амплитуда
тока в неразветвленной части цепи Im = g Um будет меньше,
чем в рассмотренных выше случаях, где
. При этом амплитуда
тока в неразветвленной части цепи Im = g Um будет меньше,
чем в рассмотренных выше случаях, где ![]()
![]()
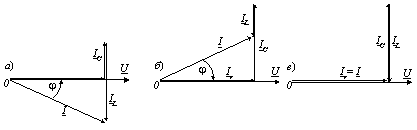
Рассматриваемое явление в цепи гармонического тока с параллельным соединением элементов r, L, С,при котором ее проводимость является активной, называют резонансом токов.
Следует отметить, что при изменении частоты приложенного к цепи напряжения полная проводимость цепи и ее характер будут изменяться, так как реактивные проводимости bL и bС являются функциями частоты.
3.4 Мощность в цепи синусоидального тока
Произведение
мгновенного значения приложенного к цепи напряжения ![]() и мгновенного
значения проходящего по ней тока
и мгновенного
значения проходящего по ней тока ![]() называют мгновенной мощностью.
называют мгновенной мощностью.
Приняв ![]() , получим:
, получим:
![]()
![]() (3.10)
(3.10)
 Из этого выражения видно, что
мгновенная мощность в цепи синусоидального тока имеет постоянную составляющую и
переменную, изменяющуюся во времени с удвоенной частотой.
Из этого выражения видно, что
мгновенная мощность в цепи синусоидального тока имеет постоянную составляющую и
переменную, изменяющуюся во времени с удвоенной частотой.
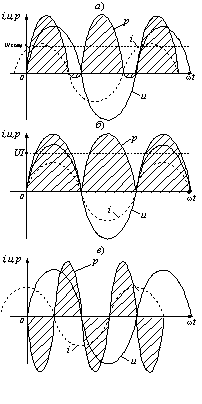
Графики мгновенной мощности для трех различных значений сдвига фаз между напряжением и током приведены на рисунке 3.13.
![]() При 0 < φ < π/2 (рисунок
3.13, а) положительные значения мощности соответствуют поступлению
энергии в цепь, где она частично запасается в электрических полях конденсаторов
и магнитных полях катушек индуктивности и частично расходуется, выделяясь в виде
теплоты в активных сопротивлениях или преобразуясь в другие виды энергии
(механическую, химическую и т.д.). Отрицательные значения мощности соответствуют
возвращению энергии к источнику. В рассмотренном случае энергия, поступающая
от источника в цепь, больше энергии, возвращаемой из цепи к источнику, так как
часть ее расходуется в цепи.
При 0 < φ < π/2 (рисунок
3.13, а) положительные значения мощности соответствуют поступлению
энергии в цепь, где она частично запасается в электрических полях конденсаторов
и магнитных полях катушек индуктивности и частично расходуется, выделяясь в виде
теплоты в активных сопротивлениях или преобразуясь в другие виды энергии
(механическую, химическую и т.д.). Отрицательные значения мощности соответствуют
возвращению энергии к источнику. В рассмотренном случае энергия, поступающая
от источника в цепь, больше энергии, возвращаемой из цепи к источнику, так как
часть ее расходуется в цепи.
![]() При φ = 0 (рисунок 3.13, б) энергия
поступает в цепь, и по отношению к ее входным зажимам такая цепь эквивалентна
активному сопротивлению. Это значит, что в резистивном элементе происходит
необратимое преобразование электрической энергии в другие виды энергии. Если же
в цепи при φ = 0 имеются конденсаторы и катушки индуктивности, например при резонансе
напряжений, то между ними происходит взаимный обмен энергией без возвращения ее
к источнику.
При φ = 0 (рисунок 3.13, б) энергия
поступает в цепь, и по отношению к ее входным зажимам такая цепь эквивалентна
активному сопротивлению. Это значит, что в резистивном элементе происходит
необратимое преобразование электрической энергии в другие виды энергии. Если же
в цепи при φ = 0 имеются конденсаторы и катушки индуктивности, например при резонансе
напряжений, то между ними происходит взаимный обмен энергией без возвращения ее
к источнику.
При φ = π/2 (рисунок 3.13, в) положительные и отрицательные участки мощности равны между собой. Это значит, что в течение одних четвертьпериодов, когда p > 0, энергия запасается (в виде энергии магнитного поля), а в течение других четвертьпериодов, когда p < 0, энергия возвращается в электрическую цепь. Такая цепь содержит лишь идеальные элементы L и С.
Среднее значение мгновенной мощности за период называют активной мощностью:
![]() .
(3.11)
.
(3.11)
Для цепи синусоидального тока после подстановки в формулу (3.11) выражения для мгновенной мощности (3.10) и интегрирования получим:
![]() .
(3.11)
.
(3.11)
т.е. активная мощность в цепи с
гармоническим колебанием равна произведению действующих напряжения, тока и
косинуса угла сдвига фаз между напряжением и током. Она характеризует энергию,
которая передается oт источника к нагрузке, где превращается в другие виды
энергии. Активная мощность измеряется в ваттах (Вт). Множитель ![]() называют коэффициентом
мощности.
называют коэффициентом
мощности.
Произведение действующих напряжения, тока и синуса угла сдвига фаз между напряжением и током называют реактивной мощностью:
![]() .
(3.12)
.
(3.12)
Реактивная мощность характеризует энергию, которая периодически циркулирует между источником и нагрузкой. Она измеряется в вольт-амперах реактивных (вар). При φ > 0, т. е. при индуктивной нагрузке, реактивная мощность положительна при φ < 0, т.е. при емкостной нагрузке, отрицательна.
Произведение действующих значений напряжения U и тока I называют полной мощностью:
![]() (3.13)
(3.13)
Полная мощность
измеряется в вольт-амперах (ВА) и характеризует предельную активную мощность
источника при ![]()
Из выражений (3.11) и (3.13) имеем ![]() т. е. коэффициент
мощности
т. е. коэффициент
мощности ![]() показывает,
какую часть полной мощности составляет активная мощность.
показывает,
какую часть полной мощности составляет активная мощность.
Условия передачи максимальной активной мощности в нагрузку.
Для определения условий передачи максимальной активной мощности в нагрузку рассмотрим цепь синусоидального тока, состоящую из источника ЭДС Е с внутренним сопротивлением zвн = rm+jxmи сопротивлением нагрузки zн = rн+jxн(рисунок 3.14). Действующий ток в рассматриваемой цепи

![]()
Активная мощность в нагрузке
![]()
![]() (3.14)
(3.14)
Из этого выражения видно, что первым условием передачи максимальной
активной мощности в нагрузку является ![]() , т. е.
равенство по значению и противоположность по знаку реактивных сопротивлений
источника и нагрузки.
, т. е.
равенство по значению и противоположность по знаку реактивных сопротивлений
источника и нагрузки.
При выполнении данного условия
выражение (3.20) принимает следующий вид: ![]() Взяв
производную от этого выражения по rн и
приравняв ее нулю, получим второе условие:
Взяв
производную от этого выражения по rн и
приравняв ее нулю, получим второе условие: ![]() , т. е.
активное сопротивление нагрузки должно быть равно активному
, т. е.
активное сопротивление нагрузки должно быть равно активному
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.