Министерство образования и науки РФ
Федеральное Агентство по образованию
ГОУ ВПО Череповецкий государственный университет
Институт металлургии и химии
Кафедра химических технологий и оборудования
по дисциплине: «химическая технология неорганических веществ»
Вариант 2
Проверил
Череповец, 2009 г.
Задача 1
Рассчитать значение константы равновесия для интервала температур t (250; 350; 450; 550; 650 оС), построить график зависимости K = f(T) и сделать вывод. Указать все способы смещения равновесия указанной реакции вправо, т.е. в сторону образования продуктов реакции.
Реакция конверсии СО:
CO + H2O « CO2 + H2, DH<0
Решение:
Константа равновесия рассчитывается по формуле:
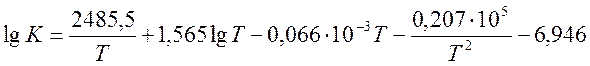, (1)
где Т – температура, К.
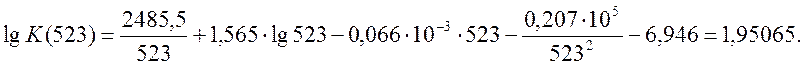
К(523) = 89,259.
lgК(623) = 1,32249; К(623) = 21,013.
lgК(723) = 0,87899; К(723) = 7,568.
lgК(823) = 0,55177; К(723) = 3,563.
lgК(923) = 0,30217; К(723) = 2,005.
Сведем полученные данные в таблицу.
Таблица 1.
|
Температура, К |
523 |
623 |
723 |
823 |
923 |
|
Константа равновесия |
89,259 |
21,013 |
7,568 |
3,563 |
2,005 |
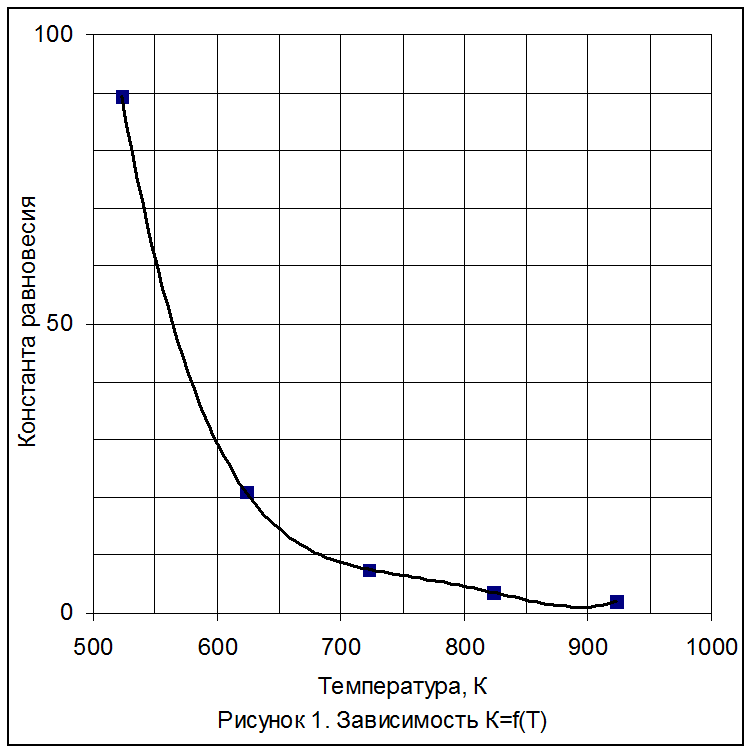
Из рисунка 1 следует, что константа равновесия сильно зависит от температуры: с ростом температуры она уменьшается, т.к. реакция экзотермическая.
Способы смещения равновесия реакции вправо, т.е. в сторону образования продуктов реакции:
1) Снижение температуры.
2) Увеличение отношения Н2О:СО. При этом возрастает степень превращения СО в продукты.
Изменение давления не влияет на положение равновесия, т.к. реакция протекает без изменения числа моль реагентов.
Рассчитать среднюю теплоемкость парогазовой смеси (ПГС), подаваемой на паровую конверсию метана, при температурах 500, 520, 560 °С. Состав ПГС, м3: CH4 – 93,8; C2H6 – 3,3; C3H8 – 1,6; N2 – 3,854; H2 – 7,416; Ar – 0,03; H2O – 370.
Решение:
Расчет теплоемкости выполняем по правилу аддитивности:
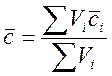, (2)
где Vi – объем компонента в смеси газов, м3; сi – средняя объемная теплоемкость компонента в смеси газов, кДж/(м3×К).
Теплоемкости компонентов смеси рассчитываем по следующим формулам в кДж/(кмоль×К):
Для H2 (при 298-3000 К):
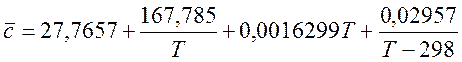(3)
Для N2 (при 298-2500 К):
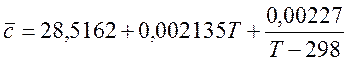(4)
Для H2O (при 298 – 2500 К):
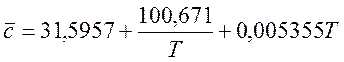(5)
Для CH4 (при 298-1500 К):
(6)
Для C2H6 (при 298-1500 К):
(7)
Для C3H8 (при 298-1500 К):
(8)
Для Ar:
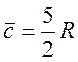, (9)
где R – универсальная газовая постоянная.
1) Расчет средней теплоемкости ПГС при 500 °С (773 К).
По формулам (3) – (9) рассчитываем теплоемкости компонентов смеси:
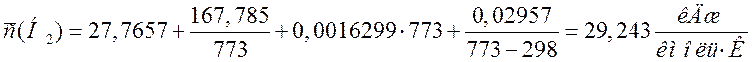
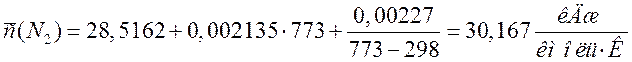
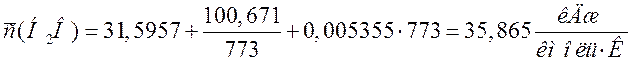
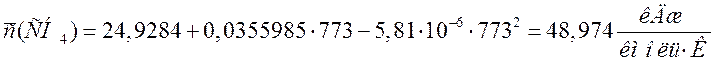
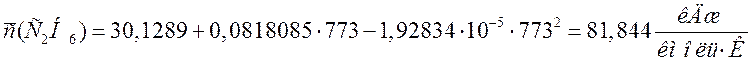
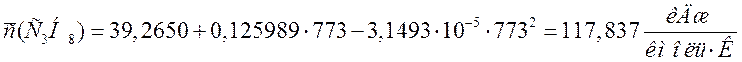
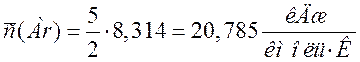
Переводим теплоемкости компонентов смеси в кДж/(м3·К). Для этого необходимо теплоемкости в кДж/(кмоль·К) разделить на молярный объем 22,4 м3/кмоль:
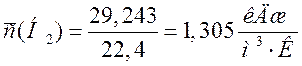
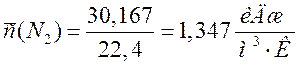
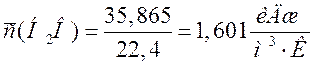
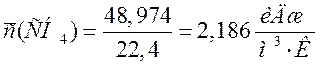
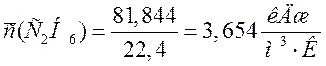
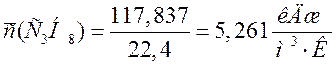
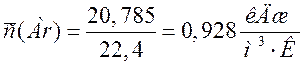
Сведем полученные данные в таблицу.
Таблица 2.
Средняя теплоемкость компонентов ПГС при температуре 773 К.
|
Компонент |
с, кДж/(кмоль·К) |
с, кДж/(м3·К) |
|
СН4 |
48,974 |
2,186 |
|
С2Н6 |
81,844 |
3,654 |
|
С3Н8 |
117,837 |
5,261 |
|
N2 |
30,167 |
1,347 |
|
Н2 |
29,243 |
1,305 |
|
Ar |
20,785 |
0,928 |
|
Н2О |
35,865 |
1,601 |
Рассчитываем среднюю теплоемкость ПГС по формуле (2):
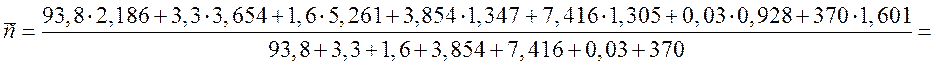
= 1,735 кДж/(м3·К).
2) Расчет средней теплоемкости ПГС при 520 °С (793 К).
По формулам (3) – (9) рассчитываем теплоемкости компонентов смеси. Результаты расчетов представлены в таблице 3.
Таблица 3.
Средняя теплоемкость компонентов ПГС при температуре 793 К.
|
Компонент |
с, кДж/(кмоль·К) |
с, кДж/(м3·К) |
|
СН4 |
49,504 |
2,210 |
|
С2Н6 |
82,877 |
3,700 |
|
С3Н8 |
119,370 |
5,329 |
|
N2 |
30,209 |
1,349 |
|
Н2 |
29,270 |
1,307 |
|
Ar |
20,785 |
0,928 |
|
Н2О |
35,969 |
1,606 |
Рассчитываем среднюю теплоемкость ПГС по формуле (2):
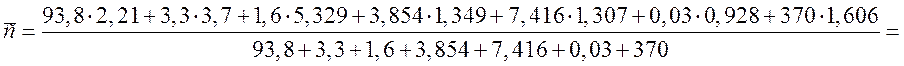
= 1,744 кДж/(м3·К).
3) Расчет средней теплоемкости ПГС при 560 °С (833 К).
По формулам (3) – (9) рассчитываем теплоемкости компонентов смеси. Результаты расчетов представлены в таблице 4.
Таблица 4.
Средняя теплоемкость компонентов ПГС при температуре 833 К.
|
Компонент |
с, кДж/(кмоль·К) |
с, кДж/(м3·К) |
|
СН4 |
50,550 |
2,257 |
|
С2Н6 |
84,895 |
3,790 |
|
С3Н8 |
122,361 |
5,463 |
|
N2 |
30,295 |
1,352 |
|
Н2 |
29,325 |
1,309 |
|
Ar |
20,785 |
0,928 |
|
Н2О |
36,177 |
1,615 |
Рассчитываем среднюю теплоемкость ПГС по формуле (2):
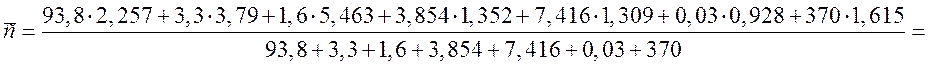
= 1,761 кДж/(м3·К).
Рассчитать степень окисления NO в NO2 для следующих исходных данных:
1. Расход нитрозных газов (НГ), нм3/ч 60000
2. Окислительный объем, м3 50
3. Давление, ат 7
4. Температура, оС 110
5. Начальная концентрация NO в НГ, % об. 4
6. Начальная концентрация O2 в НГ, % об. 5
Решение:
1) Т.к. реакция 2NO + O2 ↔ 2NO2 медленная, окисление NO будет продолжаться в течение времени пребывания газового потока в металлическом окислительном объеме. Вычислим это время пребывания τ. Для этого необходимо вначале рассчитать расход газа с учетом реальных температуры и давления. Используем уравнение Клайперона:
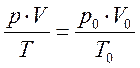(10)
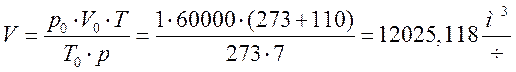
12025,118/3600 = 3,340 м3/с.
τ = 50/3,34 = 14,970 с.
2) Константа
скорости реакции окисления при 110 оС равна: К110 =
0,00171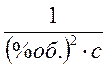 
.
3) Рассчитаем а – половину начальной концентрации NO в газе, % об.:
а = 4/2 = 2 % об.
4) Определим γ = b/а – отношение концентрации О2 к половине концентрации NO:
γ = 5/2 = 2,5
5) Вычислим левую часть уравнения:
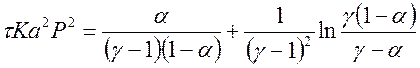, (11)
где a - степень окисления NO, доли ед.; t - время окисления, с; K – константы скорости реакции, 1/[(% об.)2×с]; а – половина начальной концентрации NO, % об.; Р – общее давление
газа, ат;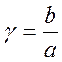 
- отношение концентрации кислорода к
половинной концентрации NO.
6) Решением уравнения (11) является такое значение величины a, при котором левая часть равна правой части. Т.к. уравнение (11) нелинейное, величину a определяем методом итераций (подбора). Приблизительные значения a установим при помощи номограммы Каржавина:
a ≈ 0,88 – 0,89.
7) Уточняем величину a подстановкой a = 0,88; 0,885; 0,89 в правую часть уравнения (11), строим зависимость и определяем a.
Таблица 5.
|
a |
0,88 |
0,885 |
0,89 |
|
Правая часть |
4,139 |
4,363 |
4,609 |
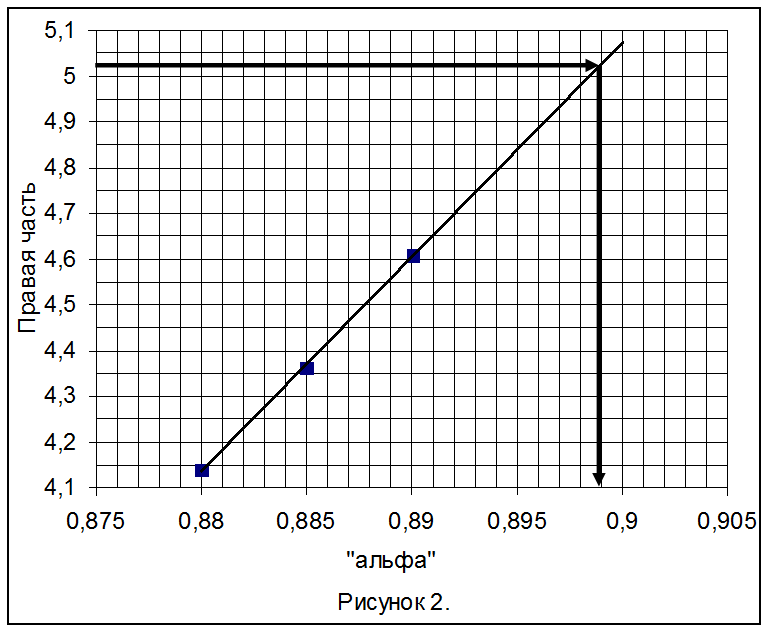
Из рисунка 2 следует: a = 0,899.
8) Рассчитаем состав нитрозного газа на входе в окислитель в нм3/ч:
NO: 0,04ּ60000 = 2400 нм3/ч;
О2: 0,05ּ60000 = 3000 нм3/ч.
Принимаем, что остальное в нитрозном газе – азот.
N2: 60000 – (2400 + 3000) = 54600 нм3/ч.
9) Изменения в составе нитрозного газа, связанные с протеканием реакции окисления NO:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
