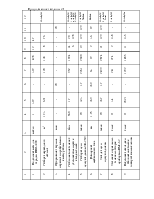
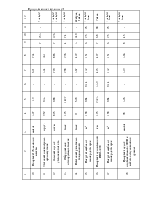
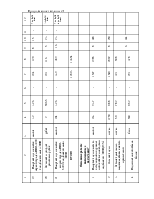
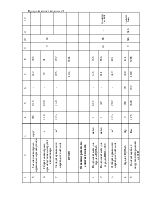
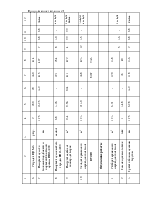
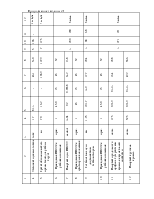
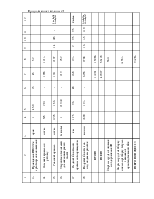
Sннк - среднее квадратическое отклонение давления колеса на рельс, обусловленное силами инерции неподрессоренных масс, возникающих соответственно при наличии изолированной неровности на колесе и при наличии непрерывных плавных неровностей на колёсах, кгс.
Sp=0.08*Pp, (29)
Рр - максимальное значение вертикальных сил, вызываемых колебаниями рессор, кгс, определяется по формуле (21), приведенной в п.1.3.2
Sинк=0.5*α0*ξ*e0*U/K, (30)
где α0 =0,433 для пути с деревянными шпалами;
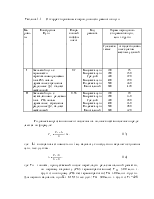
ξ - максимальный дополнительный прогиб рельса при прохождении колесом косинусоидалыюй неровности, принимается исходя из сопоставления рассматриваемой скорости движения поезда V, км/ч, с критической скоростью Vкр, км/ч:
ξ = 1,47, если V ≥ Vкр, где Vкр = 0,182 
; (31) в противном случае
(32)
где g — ускорение силы тяжести g=98 1 см/с2 ;
е0 — величина наибольшей расчётной глубины изолированной неровности на колесе, принимается равной 2/3 от предельно допустимой глубины ползуна и составляет для колёс локомотивов 0,047 см при буксовых подшипниках качения.
Среднее квадратическое отклонение Sннк, кгс, в формуле (28) определяется по формуле:
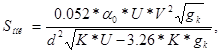(33)
где d — диаметр колеса по кругу катания, для тепловоза ТЭП 60
d=125 см.
Изгибающий момент Мдин, кгс*см, действующий на рельс в расчётном сечении, и давление на шпалу Qдuн, кгс, в расчётном сечении определяются по следующим формулам:
(34)
где l - расстояние между осями шпал: на прямом участке пути l-55 см; на кривой радиусом К=700м l=50 см.
Осевые напряжения на нижней постели подошвы рельса δп-о , кгс/см2 , и на верхней поверхности головки рельса δп-о, кгс/см2, от изгиба, кромочные напряжения в подошве δп-к, кгс/см , и головке рельса δг-к, кгс/см2, определяются по, формулам:
(35)
где Wn и Wг- моменты сопротивления рельса относительно соответственно подошвы и головки при изгибе в вертикальной плоскости, согласно для новых рельсов типа Р65 Wп=404 см и Wг=310 см ;
f и mг-к - соответственно коэффициенты перехода от осевых напряжений к кромочным в подошве и головке рельса, учитывающие горизонтальный изгиб и кручение рельса; для локомотива ТЭП 60 и новых рельсах типа Р65: на прямом участке f=1.130 и mг-к=1.342;на кривой К=700м f=1.440 и mг-к=1.466
Средние напряжения в балластном слое под шпалами в подрельсовом сечении δб, кгс/см2, и действующие напряжения под подкладкой в шпалах
δш,кгс/см2, определяются по следующим формулам:
δб=Qдин/Ω; δш=Qдин/ω; (36)
где Ω — эффективная опорная площадь полушпалы, при щебёночном балласте и деревянных шпалах Ω=2734 см2;
ω - опорная площадь рельсовой подкладки, при типе промежуточного скрепления раздельное Д2 и рельсах типа Р65 ω=589 см2.
Напряжения на основной площадке земляного полотна δш, кгс/см2,(рисунок1 ) определяются по формуле:
δh= δh'+δhc'+δhc", (37)
где δh' - напряжение от воздействия расчётной шпалы на глубине h, см, от её нижней постели, кгс/см2;
δhc'+δhc"- напряжения соответственно от воздействия первой и второй соседних с расчётной шпал, кгс/см2.
δh’=r1*δб(0.635*m*C1+1.275(2-m)*C2);
(38)
где δб - среднее давление на балласт в подрельсовом сечении расчётной шпалы, определяемое по формуле (36), кгс/см2; дополнительные индексы указывают, под какой шпалой определены значения (рисунок 1.2,1.3);
r1- поправочный коэффициент, для пути с деревянными шпалами принимается равным 0,8;
b - ширина нижней постели шпалы; для деревянных шпал
b=25 см;
h — толщина балластного слоя от нижней постели шпалы до основной площадки, см;
β1 и β2 - углы между вертикалью и прямой (рисунок 1.2), соединяющей начало и конец полосовой нагрузки с точкой, в которой определяется напряжение, рад;
C1, C2, А- расчётные параметры для железобетонных шпал.
Расчет напряжений в формуле (38) ведётся на основании расчётной схемы, приведенной на рисунке 1.3, построенной для трёхосной тележки тепловоза ТЭП 60 с расстоянием между осями колёсных пар l1=230 см.
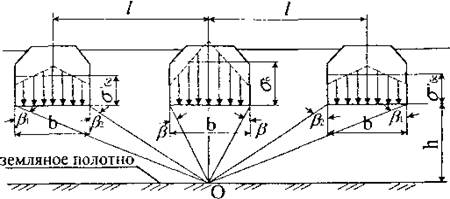
Рисунок 1.2 - Схема давления на земляное полотно от трёх cмежных шпал
Рср+λфS
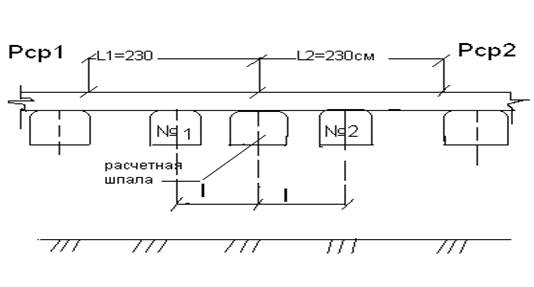Рисунок 1.3 -
Расчётная схема для определения напряжений в балласте под шпалами №1 и №2, соседними с расчетной
Согласно рисунка1.2 в формулах (38)
(39)
где ηi' и ηi"- определяются по формуле (27) и соответствуют:
η1'- положению шпалы №1 относительно силы (Рср+λф) и величине Kx=Kl;
η2' - положению шпалы №1 относительно силы Рср и величине Kx=K(li-l)',
η1" - положению шпалы №3 относительно силы (Рср+ λф) и величине Кх=К1,
η2" - положению шпалы №3 относительно силы Рср и величине Kx=K(li-l).
Расчёт среднего квадратического отклонения вертикальных
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.