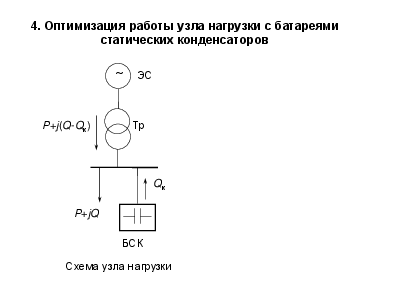








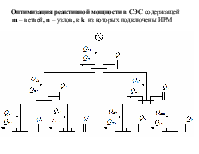


4. Оптимизация работы узла нагрузки с батареями статических конденсаторов
Энергосистема как ИРМ для потребителя характеризуется потерями активной мощности
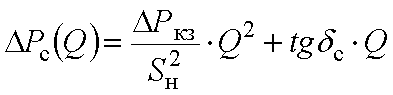
где Q – реактивная мощность энергосистемы, квар; Ркз,– потери короткого замыкания, кВт; Sн - номинальная мощность трансформатора, кВА; tgс –удельные потери активной мощности в энергосистеме, кВт/квар
БСК как ИРМ для потребителя характеризуется потерями активной мощности
![]()
где Q – реактивная мощность БСК, квар; tgбск –удельные потери активной мощности в БСК, кВт/квар.
Чтобы определить какой из двух ИРМ является более экономичным необходимо сравнить удельные потери на КРМ в различных источниках. Для БСК удельные потери на компенсацию постоянны
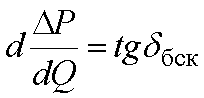
и для батарей 0,4 кВ составляют 0,004–0,005 кВт/квар.
Для энергосистемы, питающей потребителя через трансформатор
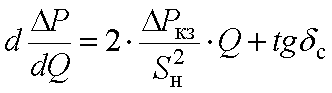
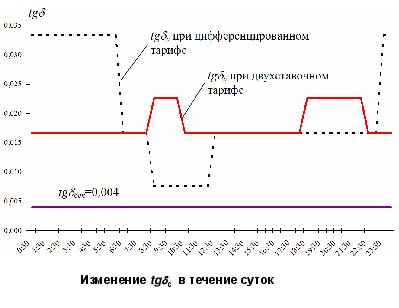
– удельные потери пропорциональны реактивной мощности и имеют постоянную составляющую tgс = bр/bа, обусловленную соотношением стоимости реактивной и активной электроэнергии, которое меняется в различных тарифных зонах суток.
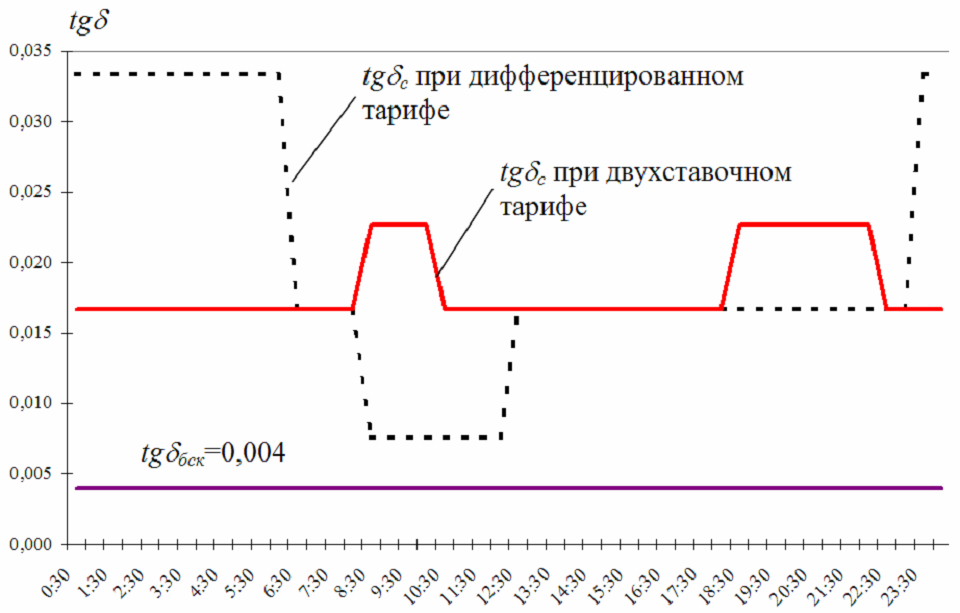
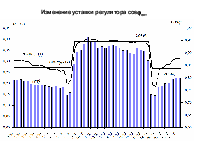
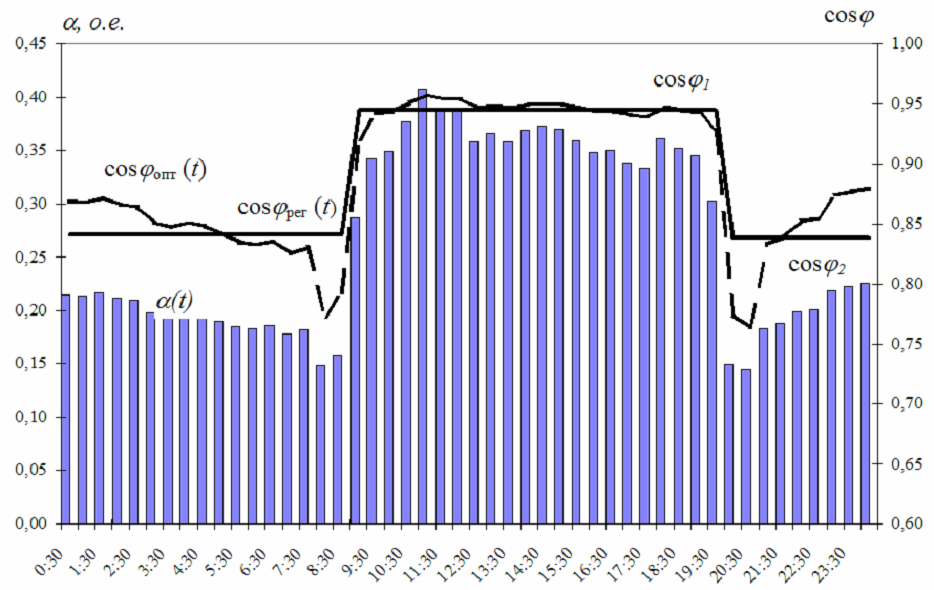
Изменение tgс в течение суток
Так как на всем суточном интервале выполняется соотношение tgбск < tgс, то для потребителя оптимальным является режим полной компенсации реактивной мощности за счет собственных источников – БСК. Автоматические регуляторы мощности БСК при этом должны поддерживать значение cos=1 в узлах подключения.
Оптимальный режим работы низковольтных БСК по критерию минимума потерь
Нагрузочные потери активной мощности в трансформаторе
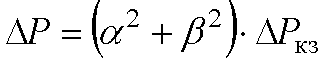
где =P/Sн – коэффициент загрузки по активной мощности Р трансформатора с номинальной мощностью Sн; = Q/Sн – коэффициент загрузки по реактивной мощности Q трансформатора с номинальной мощностью Sн; Ркз – потери короткого замыкания в трансформаторе, кВт.
Суммарные потери в системе "трансформатор-БСК» являются функцией реактивной мощности БСК
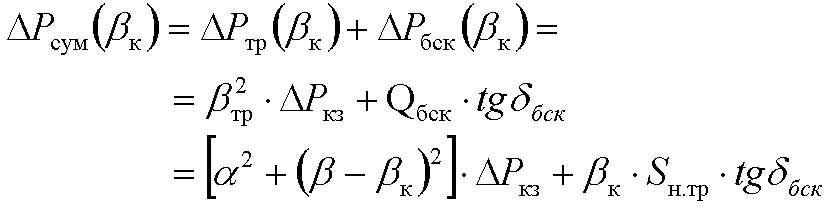
(кВт)
где tgбск – тангенс угла диэлектрических потерь в конденсаторах; к = Qбск /Sн.тр – реакт. мощность БСК, выраженная в долях от Sн.тр тр = Qтр/Sн.тр – реакт. мощность через трансф-р, выраженная в долях от Sн.тр = тр + к – реакт. мощность нагрузки на шинах, выраженная в долях от Sн.тр
Минимальные потери мощности DР→min за счет подключения БСК при = const будут при относительной мощности БСК:
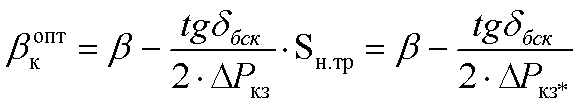
(о.е.)
С учетом того, что тр = - к , оптимальный коэффициент загрузки трансформатора по реактивной мощности:
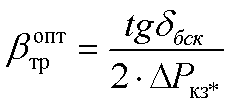
(о.е.)
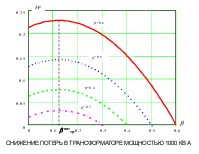
При этом снижение суммарных потерь (кВт) в трансформаторе и БСК
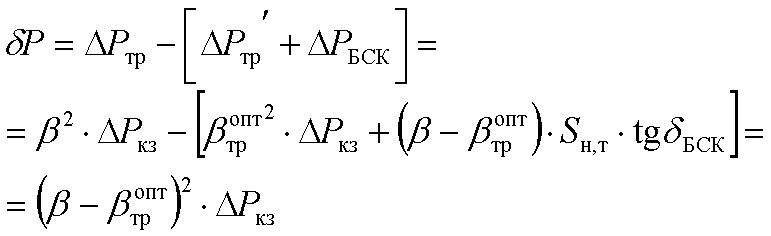
опттр
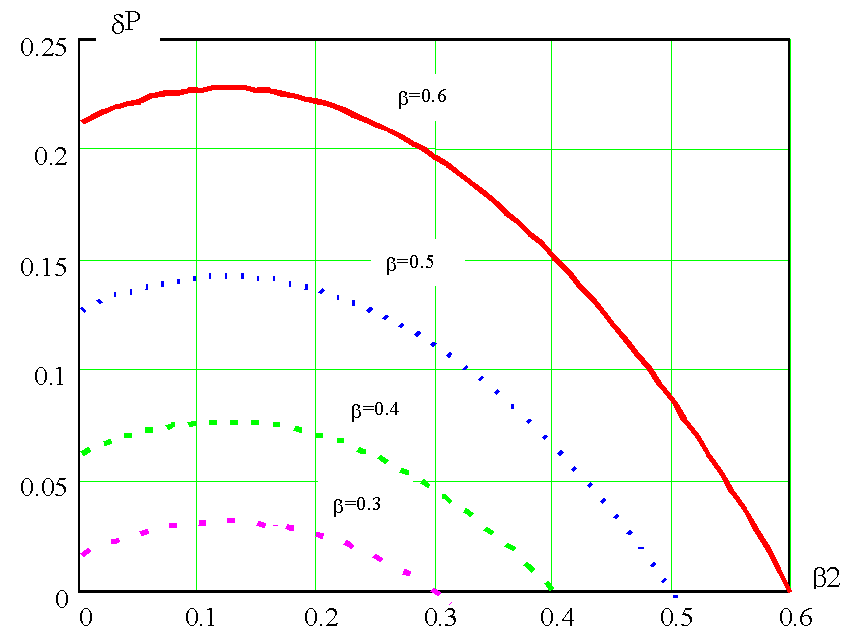
СНИЖЕНИЕ ПОТЕРЬ В ТРАНСФОРМАТОРЕ МОЩНОСТЬЮ 1000 КВА
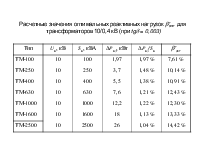
Расчетные значения оптимальных реактивных нагрузок bопт для трансформаторов 10/0,4 кВ (при tg = 0,003)
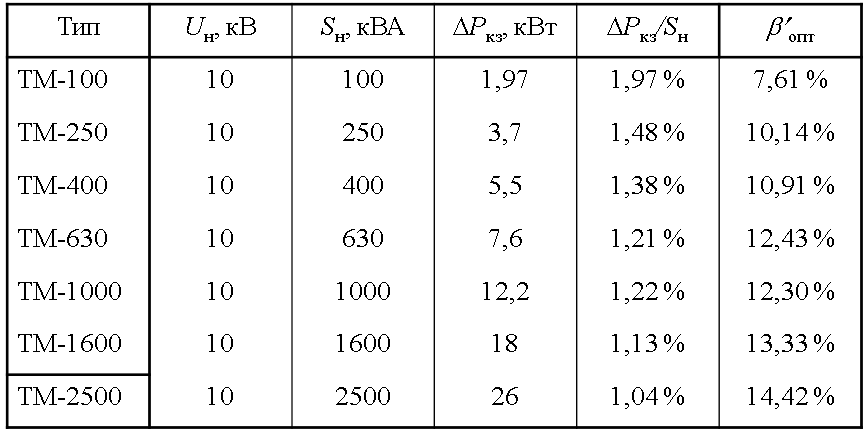
Значение оптимального cos для автоматического регулятора при известном коэффициенте загрузки по активной мощности можно определить исходя из оптимального коэффициента мощности tgопт:
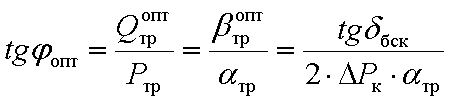
тогда
![]()
Изменение уставки регулятора cosопт
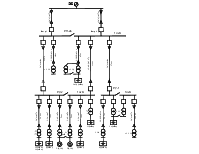
5. Оптимизация реактивной мощности в многоуровневой системе электроснабжения
Задача оптимизации режимов реактивной мощности в заводских СЭС усложняется и требует учета конфигурации электрической сети и технико-экономических показателей различных источников реактивной мощности.
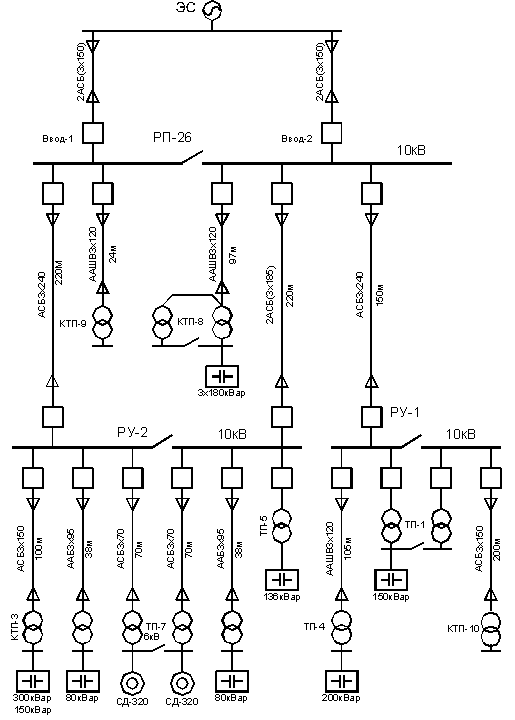
Оптимизация реактивной мощности в СЭС содержащей m – ветвей, n – узлов, к k из которых подключены ИРМ
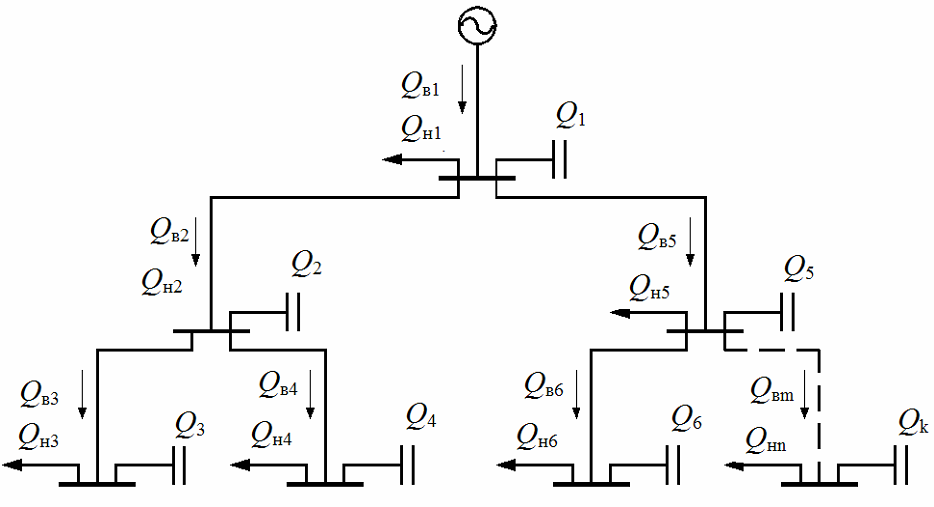
Математическая постановка задачи
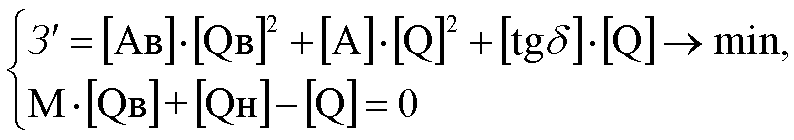
где [Ав], [А] – диагональные матрицы, характеризующие удельные потери, обусловленные активными сопротивлениями электрической сети и источников реактивной мощности
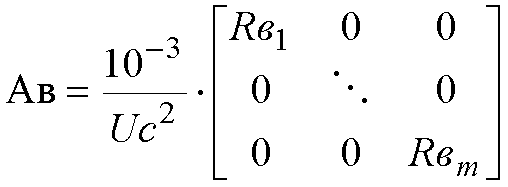
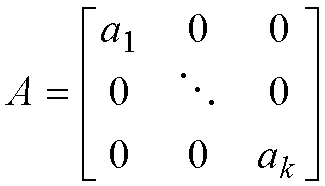
Для синхронного двигателя а=Асд/Qном2, кВт/квар2; для БСК – а=0.
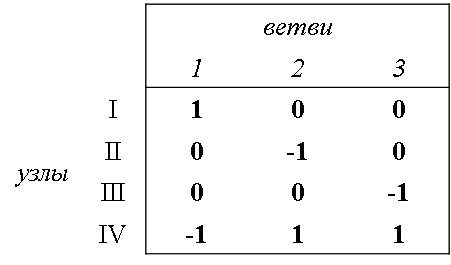
[M] – матрица соединений ветвей в узлах размерности nm. [Qв] – столбец реактивных мощностей в ветвях сети из m строк; [Qн] – столбец реактивных нагрузок в узлах из n строк; [Q] – столбец реактивных мощностей КУ в узлах сети из k строк; [tg] – столбец тангенсов углов диэлектрических потерь в КУ из k строк
Решение относительно Q по методу неопределенных множителей Лагранжа
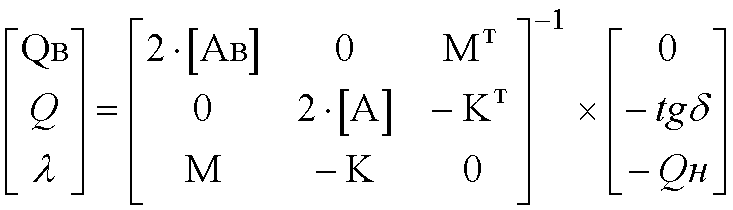
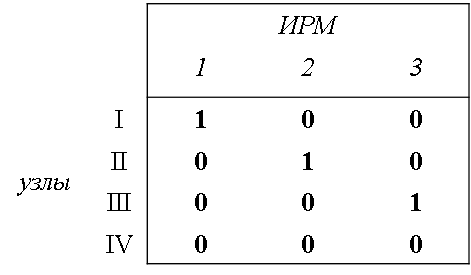
где [K] – матрица подключения источников реактивной мощности к узлам сети размерности nk. Если в n-м узле имеется k-й источник, то элемент матрицы Knk=1, в противном случае Knk= 0.
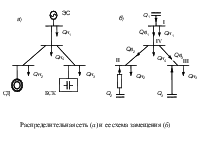
Распределительная сеть (а) и ее схема замещения (б)

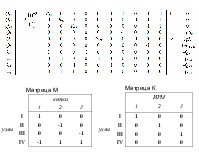
Матрица К
Матрица М
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.