Вероятность возможного недоотпуска энергии потребителю при отключении одной линии составляет 0,2; двух – 0,6, а трех – 1.
Определить вероятность того, что в результате аварийного отключения линий будет наблюдаться недоотпуск электроэнергии.
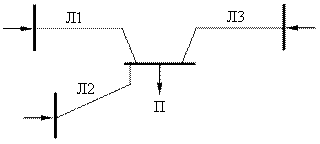
Рис. 1.5
К случайным величинам в энергетике относятся такие важные параметры режима, как спрос электрической мощности и энергии, отклонение частоты и напряжения в электрических сетях от номинальных значений, располагаемая мощность электростанций, мощности агрегатов в аварийном ремонте, длительности безаварийной работы и аварийного ремонта отдельных агрегатов, напор на гидростанциях и т.д. Знание закономерностей изменения этих случайных величин необходимо как при проектировании, так и при эксплуатации энергетических систем.
Случайные величины можно разделить на два класса: дискретные и непрерывные. Дискретная случайная величина может принимать только дискретные (разрозненные) значения, например число агрегатов, вышедших аварийно из работы. Это число в ограниченном интервале является конечным. Значение непрерывных случайных величин могут изменяться непрерывно, т.е. даже в ограниченных интервалах такие величины могут иметь бесконечно большое число значений, например ошибка прогнозирования суммарного спроса мощности. К числовым характеристикам случайных величин относятся: математическое ожидание, дисперсия, среднее квадратическое отклонение.
Математическое
ожидание ![]() для дискретной случайной величины
определим по выражению:
для дискретной случайной величины
определим по выражению:
![]() , причем суммирование происходит по всем
значениям дискретной величины
, причем суммирование происходит по всем
значениям дискретной величины ![]() , имеющим
вероятности
, имеющим
вероятности ![]() .
.
Аналогично для непрерывной случайной величины
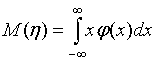
где ![]() -
плотность вероятности.
-
плотность вероятности.
В качестве меры отклонения случайной
величины от ее математического ожидания принимают величину, равную
математическому ожиданию (м.о.) квадрата отклонения случайной величины от ее
м.о., которую называют дисперсией случайной величины ![]() и обозначают через
и обозначают через ![]() :
:
![]()
Определение дисперсии для дискретных случайных величин
![]() , где суммирование распространяется на все
значения случайной величины
, где суммирование распространяется на все
значения случайной величины ![]() , имеющие
соответствующие вероятности
, имеющие
соответствующие вероятности ![]() .
.
Определение дисперсии для непрерывной случайной величины
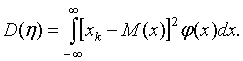
Квадратный корень из величины дисперсии называется средним квадратичным отклонением или стандартным отклонение случайной величины
![]() .
.
Пример
Пусть в энергосистеме возможны дефициты мощности 50, 100 и 150 МВт, причем вероятности этих дефицитов соответственно равен 0,001, 0,0004, 0,0002. Требуется определить м.о. недоотпуска энергии за год.
Решение. При
постоянном дефиците 50 МВт недоотпуск энергии за год составил бы 50![]() 8760 МВт
8760 МВт![]() ч, при дефиците 100 МВт - 100
ч, при дефиците 100 МВт - 100![]() 8760 МВт
8760 МВт![]() ч и т.д. Поэтому м.о.
недоотпуска.
ч и т.д. Поэтому м.о.
недоотпуска.
![]() МВт
МВт![]() ч
ч
Средние величины дают обобщающую характеристику совокупности по варьирующим признакам. Но наряду со средними величинами большое практическое и теоретическое значение имеет изучение отклонений от средних. Поэтому средние характеристики дополняют показателями измерениями отклонения от средних, т.е. показателями вариации признака.
Наиболее простым из этих показателей является показатель размаха вариации R. Его исчисляют как разность между наибольшим и наименьшим значениями варьирующего признака:
![]()
Относительной мерой вариации, позволяющей сравнивать степень варьирования признаков в вариационных рядах с разным уровнем средних является коэффициент вариации, определяемый по выражению
![]() , где
, где ![]() –
среднее квадратическое отклонение;
–
среднее квадратическое отклонение;
![]() – среднее значение (математическое
ожидание).
– среднее значение (математическое
ожидание).
Пример
Для заданного вариационного ряда вычислить дисперсию, среднее квадратическое отклонение и коэффициент вариации.
Решение. Решение целесообразно представить в виде таблицы.
Таблица 2.1. Вычисление дисперсии, среднего квадратического отклонения и коэффициента вариации
|
Группа рабочих по размеру месячной платы, тыс.ден.ед. |
Варианты (х) |
Число рабочих ( f) |
|
|
|
|
130-140 |
135 |
10 |
-30,8 |
948,64 |
9486,4 |
|
140-150 |
145 |
50 |
-20,8 |
432,64 |
21632 |
|
150-160 |
155 |
100 |
-10,8 |
116,64 |
11664 |
|
160-170 |
165 |
115 |
-0,8 |
0,64 |
73,6 |
|
170-180 |
175 |
180 |
9,2 |
84,64 |
15235,2 |
|
180-190 |
185 |
45 |
19,2 |
386,64 |
16588,8 |
|
Сумма |
- |
500 |
- |
- |
74680 |
Среднее арифметическое (математическое ожидание) вычислялось по формуле:
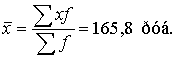
Дисперсия:
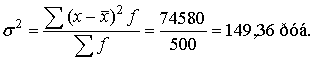
Среднее квадратическое отклонение:
![]()
Коэффициент вариации:
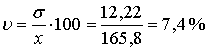
Задание
По исходным данным работы программы «WEROT» определить:
1- числовые
характеристики нагрузки Н и количество повторов ![]() ;
; ![]() ;
;
![]() и
и ![]() .
.
2 – построить многоугольник и функцию распределения вероятностей нагрузки и количества повторов.
Во всяком статистическом распределении присутствуют элементы случайности, связанные с количеством наблюдений, качеством опытов, полученными результатами. Только при очень большом числе наблюдений эти элементы случайности сглаживаются, и случайное явление обнаруживает в полной мере присущую ему закономерность. На практике число наблюдений ограничено и мы вынуждены считаться
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.