Интерполяция функций одной переменной. Интерполяционный многочлен Лагранжа. Аппроксимирующие сплайны (B-сплайны), страница 2

.

Далее, с использованием правого граничного условия вычисляется значение

  и обратной прогонкой находятся значения всех остальных величин :            

После определения всех коэффициентов  из (7) и (8) определятся коэффициенты и . Значения коэффициентов определяются из условий интерполяции .

Задание

2.1. Напишите процедуру вычисления всех коэффициентов сплайна, для хранения которых используйте двумерный массив . При реализации метода прогонки элементы матрицы , вектор правых частей  и прогоночные коэффициенты  представляйте в виде одномерных массивов. Напишите процедуру интерполяции с помощью кубического сплайна (5), используя его коэффициенты, вычисленные с помощью предыдущей процедуры. Поиск нужного интервала осуществляйте простейшим способом – перебором, начиная с первого интервала.

2.2. Для указанной выше гладкой (аналитической) функции сравните графики значений точной (реальной) погрешности для многочлена Лагранжа и кубического сплайна при одинаковом числе и расположении узлов интерполяции (равномерном и неравномерном (3)). Значения вторых производных  в (10) задайте равным их точным значениям для данной аналитической функции. Задайте значения первых производных  в (11), полагая их равными точным значениям для данной аналитической функции. Сравните погрешности при задании условий (10) и (11).

2.3. На последовательности сгущающихся равномерных узлов таблицы (n = 10, 20, 40) исследуйте порядок точности сплайна, определяя погрешность интерполяции как

2.4. Проведите аналогичное п. 1.3 исследование для описанной выше «зашумленной» функции и сделайте соответствующие выводы.

3. Аппроксимирующие сплайны (B-сплайны)

Качество приближенного представления таблично заданной функции можно значительно улучшить, если отказаться от условий интерполяции и заменить их условиями аппроксимации, т.е. условиями некоторой близости интерполирующей функции к исходной в узлах таблицы. Это вполне разумно, когда сами значения таблично заданной функции известны лишь с определенной степенью точности или когда такая функция заведомо негладкая.

Рассмотрим применение для этих целей простейших B-сплайнов второго и четвертого порядков точности соответственно. Такие B-сплайны строятся на основе т.н. «стандартного» B-сплайна, представляющего собой комбинацию гладко сопряженных полиномов третей степени

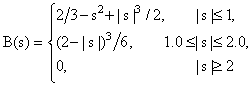                                                                                       (13)

Для случая постоянного шага между узлами интерполяции на единичном отрезке [0, 1] (от произвольного отрезка всегда можно перейти к единичному простым линейным преобразованием)  B-сплайн второго порядка записывается следующим образом

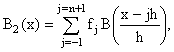                                                                                                                  (14)

где . Значения функции в дополнительных узлах  и

j = n + 1, выходящих за пределы таблицы, определяются путем ее линейной экстраполяции в эти узлы: . Погрешность интерполяции с помощью такого B-сплайна оценивается следующим образом

где - константа.

B-сплайн четвертого порядка записывается в следующем виде

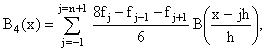                                                  (15)

значения функции в дополнительных узлах находятся также экстраполяцией

Оценка погрешность интерполяции с помощью такого B-сплайна имеет вид

где - константа.

Задание

3.1. Провести аналогичные исследования погрешности интерполяции с помощью сплайнов и  для тех же гладких и «зашумленных» функций, как это было сформулировано в задании для многочлена Лагранжа без использования оценок погрешностей приведенных выше.

3.2. Сравнить для n = 10 точности интерполяции многочленом Лагранжа, кубическим сплайном и сплайнами  и . Сделать соответствующие выводы.

Метод наименьших квадратов

Метод основан на минимизации выпуклого квадратичного функционала

                                                                      (16)

где - таблично заданная функция в N+1 узлах таблицы, - заданная аппроксимирующая функция, зависящая  от m неизвестных параметров . Минимум функционала (16) достигается в единственной точке m-мерного пространства, определяемой условиями

.

При этом получается система из m+1 уравнений для m+1 неизвестных, которая оказывается линейной, если аппроксимирующая функция линейно зависит от параметров , и нелинейной в противном случае. Обычно ограничиваются линейным представлением  , где  - некоторые  линейно независимые функции. В этом случае система линейных алгебраических уравнений для определения неизвестных параметров запишется

, где ,

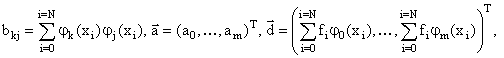
. Если в качестве базисных функций выбрать мономы, т.е. , то система уравнений примет вид

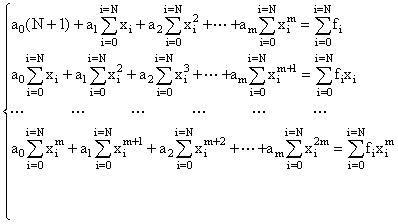                                               (17)

   Задание 3

1.  Провести аналогичные исследования погрешности интерполяции для тех же гладких и негладких функций, как это было сформулировано в задании для многочлена Лагранжа. 

2. Сравнить для n = 10 точности интерполяции многочленом Лагранжа, сплайнами , и методом наименьших квадратов. Сделать соответствующие выводы.