Исследование аварийных ударных воздействий на строительные конструкции

Введение

Среди различных аварийных ситуаций в последние годы значительно возросло число аварийных ударных воздействий на строительные конструкции. По степени поглощенной энергии различают удары резкие, промежуточной резкости, нерезкие. В первом случае поглощенная конструкцией часть подводимой энергии значительно превышает поглощенную ударником и, таким образом, ударник при резких ударах может считаться недеформированным. Во втором случае доли энергии, поглощенные ударником и конструкцией, сопоставимы. При нерезких ударах энергия, поглощенная ударником, значительно превышает долю энергии, поглощаемая конструкцией. При расчете конструкции в первых двух случаях необходимо учитывать взаимодействие ударника с конструкцией. В последнем случае конструкция может считаться недеформируемой в процессе соударения, а действие ударника может быть заменено импульсивной локальной нагрузкой.

1.  Параметры ударных нагрузок.

Эффект удара зависит от формы носовой части ударника (индентора), угла, составляемого осью ударника с поверхностью конструкции, от отношения диаметра ударника и толщины конструкции и ряда других параметров. Ударные нагрузки оценивают величиной импульса I.

Где М_s – масса ударника; V₀- скорость удара; максимальная интенсивность и продолжительность ударной нагрузки; K_F – коэффициент, характеризующий форму импульса K_F=1 для прямоугольного и K_F =0,5 для треугольного.

В промышленных зданиях параметры ударов, возникающих в результате аварий кранового оборудования, обычно определяются паспортными данными кранов. Для одноэтажных зданий с ж\б каркасом М_s≤75т, многоэтажных М_s ≤10 т, скорость удара зависит от высоты Н подъема крюка крана относительно перекрытия  V₀= K_FR, где g – ускорение свободного падения, K_FR - коэффициент, учитывающий потери энергии.

2.  Реакция на удар.

Балки и рамы.

На рисунке  показано трещинообразование в защемленных балках и рамах в зоне под ударником. В опорных сечениях образуются нормальные трещины в верхних зонах, которые впоследствии могут сильно раскрываться.

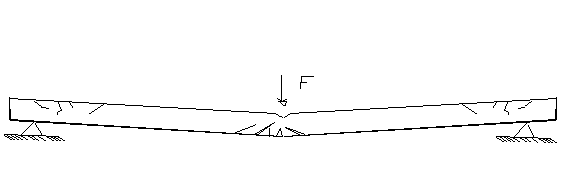
трещинообразование в защемленной балке

После достижения динамического предела текучести в нижней продольной арматуре в зоне с трещинами шарнирно-опертой балки возникает пластическая деформация.

Расчет ж\б балок производится только на общее действие удара. При резких ударах необходимо учитывать взаимодействие  ударника с конструкцией, т.е. должен быть установлен контактный закон, связывающий силу удара F с прониканием ударника в конструкцию.

Контактный закон для плоского индентора может быть представлен в виде:

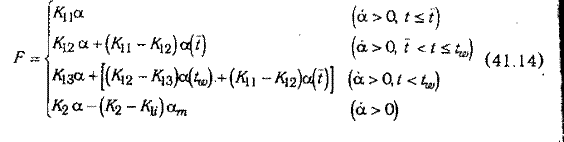
где K_1i- тангенсы соответствующих углов наклона участков ветви нагрузки; K₂- тангенс угла наклона ветви разгрузки; t-момент достижения текучести в хомутах.

Если     стадией     до     образования     трещин     пренебречь (вследствие ее малого влияния), то будем иметь (рис.41.13,б):

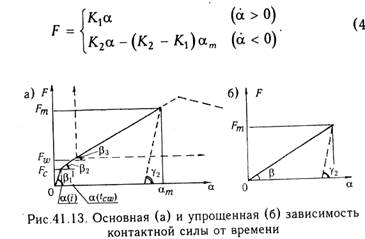
Коэффициент К₁ характеризует сопротивляемость контактной зоны внедрению ударника и зависит, помимо упомянутых ранее факторов, от выбранной расчетной модели. В наиболее общем случае целесообразно использовать расчетную модель контактной зоны, показанную на рис.41.14. В данной модели пренебрегают по малости сопротивлением бетона на боковых гранях (за пределами хомутов), а также зацеплением бетона по берегам наклонных трещин.

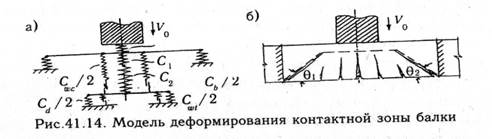
Расчеты показали, что основной вклад в сопротивление контактной зоны вносит балочка, образованная бетоном над трещиной и воспринимающая изгибно-сдвиговые деформации.

Поэтому можно принимать  где η-Коэффициент формы сечения, С_гв=0,4Е_b - модуль сдвига бетона, А - площадь поперечного сечения; φ_сгс - коэффициент, учитывающий    влияние    трещин    на    деформации    сдвига, φ_сгс =4,8

Согласно опытным данным движение простейшей шарнирно-опертой балки разбивается на три стадии: 1) до образования трещин; 2) после образования трещин до достижения динамического предела текучести в продольной арматуре (в дальнейшем эту стадию будем называть условно-упругой); 3) после достижения текучести в продольной арматуре до достижения предельных осевых деформаций в бетоне сжатой зоны или до разрыва продольной арматуры (пластическая стадия).

Стадия до образования трещин заканчивается в один и тот же момент времени как с позиций общего, так и местного действия удара. До этого момента балка рассматривается как сплошной упругий элемент. Влиянием этой стадии на местное деформирование контактной зоны и на общее упруго-пластическое деформирование балки при обычных соотношениях h/lтакже невелико и им можно пренебречь. Таким образом, в дальнейшем эта стадия из рассмотрения исключается.

Условно-упругая стадия. После образования трещин изгибная жесткость В₁  в контактной зоне падает и может быть

Где z₁=h₀-x₀/2 – плечо внутренней пары; ω – коэффициент полноты  эпюры напряжении в бетоне сжатой зоны (при динамических нагружениях ω =0,5); Ψ_s и Ψ_b - коэффициенты неравномерности деформаций в продольной арматуре и бетоне сжатой зоны (по опытным данным Ψ_s = Ψ_b =1); v = 0,45 - коэффициент упругих деформаций бетона; h₀ = h₀- α ; h₀- рабочая высота сечения.

В остальных сечениях (без трещин) жесткость определятся по формуле        В_о = E_bJ_red,  где  J_red- приведенный момент инерции сечения