Исследование аварийных ударных воздействий на строительные конструкции, страница 2

Для получения уравнений движения воспользуемся уравнением Лагранжа          2-го рода

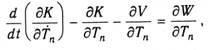
где К, Vи W- кинетическая, потенциальная энергия и   работа внешней нагрузки; Т_п - обобщенные координаты система.

В формуле, соответствующей кинетической энергий   ударника,

первое слагаемое характеризует затраты на изгиб балкой, второе - на перемещение у + а; m - погонная масса балки;  х - координата точки приложения ударной нагрузки.

Для балок, в которых допускается пластическая стадия работы, может быть использовано упрощенное представление потенциальной энергии, в котором жесткость принимается постоянной, равной В₁. В этом случае

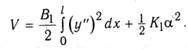
Зададим выражение для прогиба

Получим систему уравнений движения относительно неизвестных функций времени Т_п в матричной форме

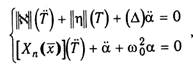
Последнее уравнение в системе описывает движение ударника на перемещении у + α. Изгибающие моменты и поперечные силы определяют по известным формулам

Уравнения  справедливы до момента времени tдостижения максимального внедрения ударника или до момента времени t₁, когда в продольной арматуре будет достигнут динамический предел текучести. Момент Iопределяется из условия å(t) = 0, где а - решение системы, a t₁находят из условия М(х,t₁)=M_ud, где M_ud- предельный упругий момент в сечении (с одиночной арматурой)

 в контактной зоне начинается разгрузка, и в достаточно последнее слагаемое заменить на сумму

Последнее уравнение  приобретает вид

Если контакт ударника с балкой прекращается в момент времени , то далее балка продолжает свободное движение. Момент времени  может быть найден из условия

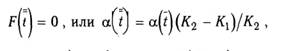
При t > t₁наступает следующая - пластическая стадия. Рассмотрим движение балки, армированной сталью класса А-II или А-Ш, имеющей площадку текучести. Расчетная схема для этой стадии представляется в виде механизма из жестких звеньев, соединенных пластической зоной, которая заменяется сосредоточенным пластическим шарниром

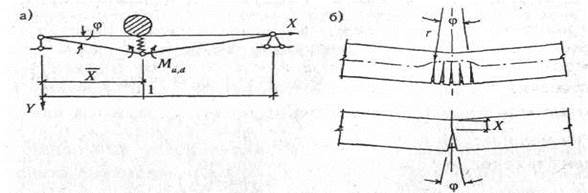
Расчетная схема балки в пластической стадии

Значение прогиба балки в этой стадии будем искать в виде

Для получения уравнений движения вновь используем уравнения Лагранжа. Предполагая, что к началу пластической стадии в контактной зоне продолжается нагружение, запишем выражения для кинетической и потенциальной энергии системы

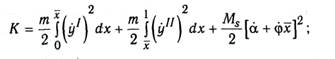
В последнем выражении первое слагаемое в правой части представляет работу сосредоточенного изгибающего момент M_udна угле раскрытия в пластическом шарнире, второе - потенциальную энергию деформирования контактной зоны. Получим систему уравнения движения

Перенося начало отсчета времени в начало пластической стадии, запишем начальные условия в виде

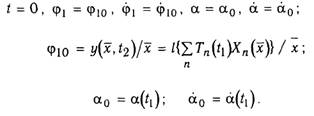
Начальную угловую скорость ф₁₀ определяют из условия равенства количества движения балки в конце условно-упругой в начале пластической стадии

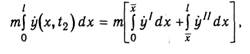
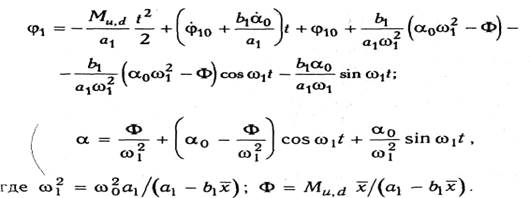
Если в контактной зоне в момент времениначинается разгрузка, то присистема уравнений движения имеет вид

- определяется, как и ранее, с учетом возможного снижения осевой прочности и размеров сечения. С учетом переноса начала отсчета   времени

Решение имеет вид при следующих заменах:

Система  будет справедлива до момента tпрекращения контакта ударника с конструкцией, находимого из условия , где α- решение. После прекращения контакта балка движется свободно по уравнению движения

при начальных условиях

Его решение

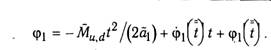
Уравнения справедливы до момента t_m достижения абсолютного максимума перемещения балки, который может быть найден из условия. После этого неразрушившаяся балка совершает колебания относительно положения,  определенного максимальным пластическим прогибом . Для проверки прочности балки максимальный угол необходимо подставить в уравнение

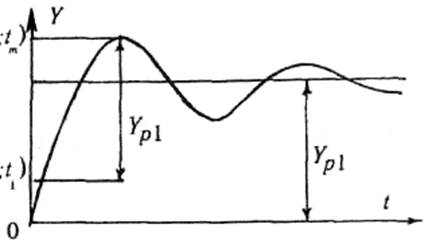Зависимость упругопластического   прогиба   плиты от времени

Если балка переходит в пластическую стадию, когда в контактной зоне уже началась разгрузка, необходимо в качестве годной рассмотреть систему при начальных условиях, а если к началу пластической стадии контакт ударника с балкой прекратился, то справедливо уравнение, при начальных условиях

Должна быть обеспечена прочность по наклонным сечениям в пролете согласно, где Q(x,t) в условно-упругой стадии находят по, а в пластической — из выражений

Где α и φ₁ представляют решения уравнений представленных ранее. Разрушение в пролете по наклонным сечениям обычно проходит до образования пластических зон, поэтому необходимость в определении Q₁, Q_II отпадает.

Расчет статически неопределимых балок производят аналогично изложенному выше. В упруго-пластической стадии в расчет вводят формы колебаний, соответствующие реальным условиям закрепления. В пластической стадии необходимо учитывать последовательность образования пластических шарниров на опорах и в пролете, аналогично расчету на взрывные нагрузки. .

Наряду с изложенным, близкие к опытам результаты дают методы расчета, основанные на дисково-связевых моделях. На рис.41.17 даны примеры таких моделей шарнирно-опертых балок, в которых взаимодействие ее частей отражено в связях, моделирующих поведение бетона, продольной и поперечной арматуры. Такие модели позволяют получить не только интегральные характеристики процесса деформирования (прогибы и углы поворота), но и изменение напряжений во времени в критических сечениях.

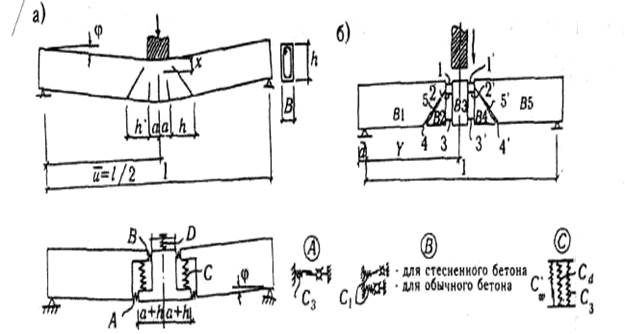
Дисково-связевые модели балок