Введение
В представлении большинства линейная регрессия (linear regression) ассоциируется с вычислением углового коэффициента и точки пересечения с осью ординат аппроксимирующей пряной, которая лучше всего описывает рассматриваемые данные. Однако это только начальные понятия, относящиеся к линейной регрессии. В термине линейная регрессия слово "линейная" означает, что уравнения, которые используются для описания данных, должны быть линейными относительно своих коэффициентов; при этом вовсе не подразумевается, что график зависимости должен быть прямой линией или что в уравнении должны фигурировать только два коэффициента (угловой коэффициент и точка пересечения прямой с осью ординат).
1. Выполнение линейной регрессии с помощью функций Excel
В том случае, когда нужно вычислить угловой коэффициент (slope) и найти точку пересечения с осью ординат (intercept) прямой линии, которая лучше всего описывает набор данных, очень полезными окажутся функции Excel НАКЛОН() и ОТРЕЗОК(). Добавив к ним функцию КВПИРСОН(), вычисляющую квадрат коэффициента корреляции (coefficient of determination), получим простейший набор, позволяющий решить многие задачи по анализу данных.
1.2 Простой пример
В качестве примера проанализируем простой набор данных, включающий в себя значения температуры и времени (рис.1). Этот пример позволит ознакомиться с основными приемами проведения регрессионного анализа в Excel.
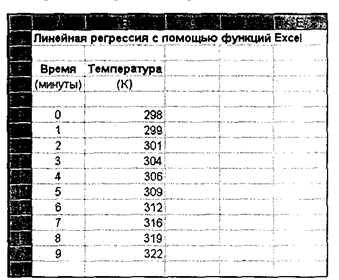
Для определения углового коэффициента прямой линии, лучше всего описывающей данные, предназначена функция НАКЛОН(). У функции НАКЛОН() два аргумента, расположенные в таком порядке: диапазон ячеек, содержащий значения (значения зависимой переменной (dependent variable)), и диапазон ячеек, содержащие значения .v (значения независимой переменной (independent variable)) (рис.2).
В данном случае изучается зависимость температуры от времени, а не наоборот, поэтому зависимой переменной является температура (ячейки В6:В15), а время (ячейки А6:А15) считается независимой переменной.
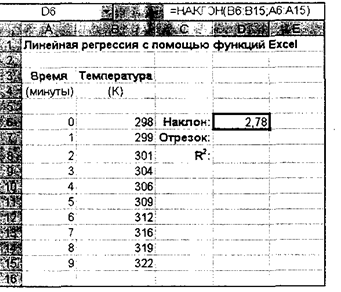
Аналогично, точку пересечения прямой регрессии с осью ординат можно найти с помощью функции OTPE3OKQ с теми же аргументами (рис.3).
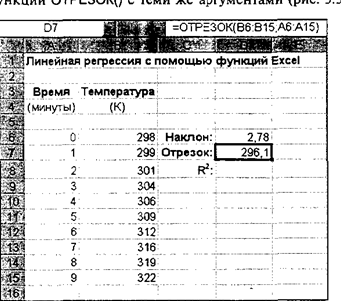
Квадрат коэффициента корреляции (R2) вычисляется с помощью функции КВПИРСОН() с теми же аргументами, что и у двух предыдущих функций (рис. 4).
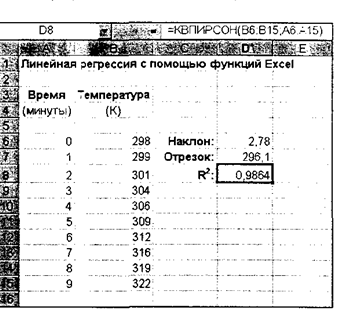
Полученные результаты свидетельствуют о том, что прямая, лучше всего описывающая данные, имеет угловой коэффициент Ь1 = 2,7758 К/мин и пересекает ось ординат в точке Ьо = 296,1 К. Значение R2равно 0,9864 (эти величины извлечены непосредственно из данных, без построения диаграммы).
Таким образом, вычислен угловой коэффициент, найдена точка пересечения линии регрессии с осью ординат, а также величина R2. Насколько хорошо прямая линия описывает данные? Чтобы ответить на этот вопрос, необходимо построить диаграмму с данными и линией регрессии, позволяющую визуально убедиться в степени их совпадения.
2. Выполнение линейной регрессии с помощью линии тренда
Регрессионный анализ в Excel невероятно прост. Как только данные представлены в графическом виде, регрессия выполняется с помощью нескольких щелчков мыши, поэтому регрессия с использованием прямой часто применяется несмотря на то, что зависимость между переменными не линейная, а более сложная. Сформулируем практическое правило: всегда следует строить диаграмму, на которой представлена кривая регрессии и данные, чтобы можно было визуально оценить степень совпадения. В том случае, когда регрессия проводится с помощью линии тренда, кривая регрессии автоматически добавляется на диаграмму с соответствующими данными.
2.1. Выполнение простейшей линейной регрессии с помощью прямой
Для выполнения линейной регрессии, в процессе которой вычисляется угловой коэффициент и точка пересечения аппроксимирующей прямой с осью ординат, вычисляются различные суммы, включающие в себя значения х (независимой переменной) и y (зависимой переменной). С помощью этих сумм и уравнений (1) можно было бы вычислить угловой коэффициент Ь1 и найти точку пересечения прямой регрессии, лучше всего описывающей данные, с осью ординат (b0). Однако в этом нет нужды, так как формулы.1 встроены в Excel.
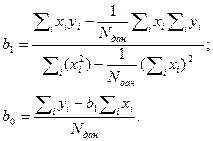 (1)
(1)
В уравнениях 5.1 обозначение I, подразумевает суммирование по всем данным, а индекс i, нумерующий результаты измерений, пробегает значения от 1 до количества всех данных Nдан.
При построении на диаграмме линии тренда Excel автоматически вычисляет асе необходимые суммы, затем находит значения коэффициентов b1, и bо, а также квадрат коэффициента корреляции (достоверность аппроксимации) R2. Благодаря тому, что линия тренда строится на диаграмме, можно убедиться, насколько хорошо она описывает данные. Уравнение линии тренда и значение R2 по умолчанию на диаграмме не отображаются. Чтобы отобразить эту информацию, следует воспользоваться вкладкой Параметры диалогового окна Пиния тренда.
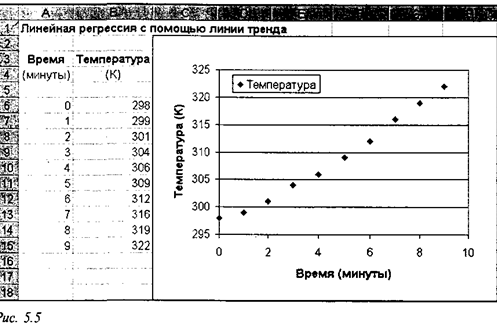
Продемонстрируем применение линии тренда на примере данных, рассмотренных в предыдущем разделе. Первый шаг в использовании линии тренда для получения уравнения регрессии — это представление данных в графическом виде на точечной диаграмме (рис. 5).
Примечание. Обычно данные на точечной диаграмме отмечаются маркерами, но не соединяются кривыми, чтобы лучше было видно, насколько близко от них проходит аппроксимирующая линия.
Затем щелкните правой кнопкой мыши на любом из маркеров данных и во всплывающем меню выберите команду Добавить линию тренда... (рис. 6).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.