Разработка проекта железобетонных и каменных конструкций шестиэтажного здания с неполным каркасом (высота этажа – 3,3 м)

2003 определяем характеристики для арматуры В500:

R_s=415 МПа.

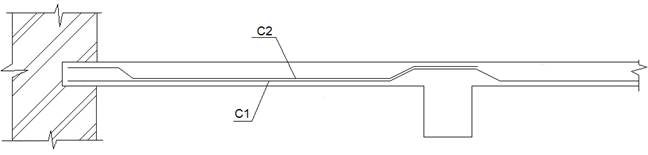
Рис. 1.3 Армирование монолитной плиты.

Выполним подбор сечений   продольной арматуры сеток.

В средних пролетах, окаймленных по контуру балками, и на промежуточных опорах:

h₀ = h – a = δ – a =80 - 12,5= 67,5 мм =0,0675 м

α_m =М₂ / (R_в* в*h₀²) =3,24 кНм / (13050 кН/м² * 1 м *0,0675² м²) = 0,054,  где

R_в = R_в ^снип * γ _в2 = 13,05 МПа

R_в ^снип    см. [2]  таб 13

γ _в2     см. [2]  таб 15

ξ = 1 - √(1 - 2 α_m) = 1 - √(1 – 2*0,054) =0,056 < ξ_R= 0,656 [1]  таб. IV.2

η =1 – ξ /2 =1 – 0,056/2 = 0,972

R_s* A_s = M₂ / (η* h₀) = 3,24 кНм / (0,972 *0,0675 м) = 49322 Н

По [1] прил.III принимаем сетку С1 № 24

5 В-500 – (х150) +100      

5 В-500 – 150

с фактической несущей способностью продольной арматуры:

R_s* A_s = 49810 Н  > 49322 Н.                           

В первом пролете и на первой промежуточной опоре:

h₀ = h – a = δ – a =80 - 16,5= 63,5 мм =0,0635 м

α_m =М₁ / (R_в* в*h₀²) =4,21 / (13050 * 1  *0,0635² ) =0,08

ξ = 1 - √(1 - 2 α_m) = 1 - √(1 – 2*0,08) =0,084 < ξ_R= 0,656 [1]  таб. IV.2

η =1 – ξ /2 = 1 - 0,084/2 = 0,958

R_s* A_s = M₁ / (η* h₀) = 4,21 / (0,958 * 0,0635 м) = 69272 Н

R_s* A_s' =69272 – 49810 = 19462

По [1] прил.III принимаем сетку С2 № 48

4 В-500 – 200      

8 А-400 - 150

С фактической несущей способностью продольной арматуры

R_s* A_s  = 23980 H >19462 Н.

Расчет второстепенной балки

За расчетную схему принимается многопролетная неразрезная балка, опирающаяся на главную балку (рис.1.4).

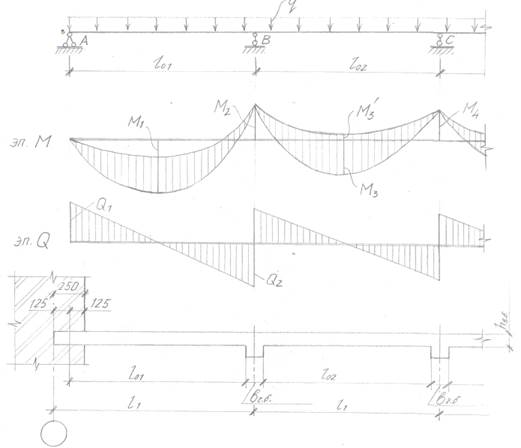
Рис. 1.4 Расчётная схема второстепенной балки.

Расчетный пролет балки:

ℓ₀₁  = ℓ₁ – 250/2 -  b_г.в./2 =5600 - 125 – 400/2 = 5275 мм.

ℓ₀₂  = ℓ₁ -  b_в.б =5600-400=5200 мм.

Определяем нагрузку на второстепенную балку:

Постоянные нагрузки:

- от веса плиты и конструкции пола:

q₁ = 3,4 кН/м² (см. табл. 1.1);

-от собственного веса балки:

q₂ = ( h^б – δ^пл)· b^б ∙ ρ ∙ γ_f = (0,45 – 0,08)· 0,15· 25· 1,1=1,53 кН/м²;

Временные нагрузки:

q₃ = 12 кН/м² (см. табл. 1.1).

Погонная нагрузка:

q=(3,4 + 12)*2,2*1 + 1,53=35,41 кН/м.

Изгибающий момент в первом пролете:

М₁ = q· ℓ₀₁²  /11 = 35,41 · 5,275² /11 = 89,57 кНм.

Изгибающий момент на первой промежуточной опоре:

М₂ = q· ℓ₀₁²  /14 = 35,41 · 5,2² /14 =68,39 кНм.

Максимальная поперечная сила (на первой промежуточной опоре слева):

Q_max =Q₂ = 0,6 q · ℓ₀₁  = 0,6 · 35,41 · 5,275=112,07 кН.

Рассчитаем сечение в пролете:

h_f' = δ = 80 мм;

h= h_в.б =450 мм;

h_о = h_в.б  -а_з = 450-50 = 4500 мм;

h_f' =  80 мм >0,1 h = 0,1*450 мм = 45 мм, тогда:

b_f' ≤ с = ℓ₃ - b^б = 2200-150=2050 мм.

b_f'  ≤ ℓ₃ /3 + b^б = 2200/3 + 150 =883,33 мм.

Принимаем  b_f' =883,33 мм.

Определяем положение нейтральной оси, для чего проверяем условие:  

М₁ ≤ R_в ∙ h_f' ∙ b_f' ∙ (h₀ - h_f'/2)

М₁ = 89,57 кНм < 13050 ∙ 0,08 ∙ 0,883 ∙ (0,40- 0,08/2) =119,47 кНм.

Условие выполняется, следовательно, граница сжатой зоны проходит в полке двутаврового сечения. Рассчитываем сечение как прямоугольное, сечением 883,3 мм х 450 мм.

α_m =М₁ / (R_в· b_f' · h₀²) =89,57/ (13050· 0,8833· 0,40²) =0,049;

ξ = 1 - √(1 - 2 α_m) = 0,050 ≤ ξ_R= 0,604

η =1 – ξ /2 =0,975

Требуемая по расчету площадь продольной рабочей арматуры:

A_s = M₁ / (R_s ∙ η ∙ h₀) = 89,57/ (225 ∙ 10³ ∙ 0,975 ∙ 0,450) =907,3 мм², где:

R_s = 225 МПа = 225000 кН/м²   для арматуры А-240 по таб. 5.8 СП 52-101-2003;

По сортаменту стержневой и проволочной  арматуры принимаем 2 ø 25 А-240

А_s =982 мм²  >  А_s^треб  = 907,3 мм²

Рассчитаем сечение на опоре:

h₀ = h - а = 450 - 40 = 410 мм =0,41 м

α_m =М₂ / (R_в ∙ b_в.б ∙ h₀²) =68,39 кНм / (13050 кПа · 0,15 · (0,41 м)²) =0,208

ξ = 1 - √(1 - 2 α_m) = 0, 236< ξ_R= 0,604

η =1 – ξ /2 =0,882

A_s = M₂ / (R_s ·  η ·  h₀) = 68,39 / (225 · 10³ · 0,882· 0,41)= 840,54мм²

Принимаем 5 ø 14 А-240    с А_s =769 мм²  >  А_s^треб = 570 мм²

Выполним расчет прочности наиболее опасного сечения балки на действие поперечной силы.

По прил.II  [1] из условия сварки принимаем поперечные стержни диаметром 5 мм класса А-240 ( т.к. диаметр 8 мм). A_sw = 101 мм².

Определяем шаг:

- на опоре:

s₁ ≤ h_о /3 =450/3=150 мм

s₁ ≤ 300 мм принимаем s₁=150 мм.

- в середине пролёта:

S₂ ≤ 3h_о /4 =337,5 мм

S₂ ≤ 500 мм принимаем s₂=330 мм.

Проверяем прочность наклонной полосы:

Q_н.с ≤  Q_b+ Q_sw,

Где Q_b – поперечная сила, воспринимаемая бетоном,

Q_sw –сила, воспринимаемая поперечными стержнями.

Q_sw = 0,75 · q_sw ∙ c

q_sw = R_sw ∙ A_sw / s₁ = 175 МПа ∙ 101 мм² /150 мм =  117,83 кН/м.

Проверяем условие:

q_sw ≥ 0,25 · R_bt · b =0,25 · 1050 кПа · 0,15 м = 39,37 кН/м.

условие выполняется, следовательно,

М_b = 1.5 ∙ R_bt · b ∙ h₀² = 1.5 ∙ 1050 кПа ∙ 0,15 м ∙ ( 0,41 м)² = 39,71 кНм.

Q_max = 112,07 кН,

q = 35,41 кН/м,

q₁ = q – 0,5 · v = 35,41 – 0,5· (12· 2,2· 1) = 22,21 кН/м.

Так как q_sw / R_bt · b = 117,83 / 1050 · 0,15 = 0,74 < 2, то с =√(М_b / q_I)  = √ (39,71 / 22,21 = 1,34 м, в то же время с ≤ 2 h₀ = 820 мм, с ≥  h₀ = 410 мм.

Принимаем с=0,82 м.

Тогда Q_sw = 0,75 · 117,83 ∙ 0,82 = 72,47 кН.

Q_b =  М_b / с = 39,71 / 0,82 = 48,73 кН.

Q_н.с =   Q_max - q₁· с = 112,07 – 22,21· 0,82 = 93,86 кН.

Получаем:

Q_н.с  = 93,86 ≤  Q_b+ Q_sw = 48,73 + 72,47= 121,12 кН.

Условие выполняется, следовательно, прочность наклонной полосы обеспечена.

Результаты проверки ЭВМ см. приложение1.

Схемы армирования монолитной плиты и второстепенной балки  см. графическую часть  лист 1.

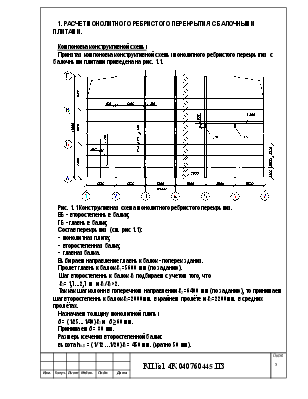
2  РАСЧЕТ СБОРНОГО БАЛОЧНОГО ПЕРЕКРЫТИЯ.

Расчет плиты с овальными пустотами

Компоновка конструктивной схемы перекрытия

Данные для проектирования:

Шаг колонн в продольном направлении                                -  5,6 м

Временная нормативная нагрузка                                          - 10,0 кН/м²

Постоянная нормативная нагрузка от массы пола                - 1,0 кН/м²

Класс бетона для сборных конструкций                                  В25

Класс предварительно напряженной арматуры                     А - 1000

Способ натяжения арматуры на упоры                                   электротермический

Условия твердения бетона                                                       естественные

Тип плиты перекрытия                                                              <круг.>

Вид бетона для плиты                                                              лёгкий

Влажность окружающей среды                                                70 %

Класс ответственности зданий                                                 I   

Находим BF’ = (6400-400)/3 = 2000 мм.

По результатам компоновки конструктивной схемы перекрытия принята номинальная ширина плиты 2000 мм.

Определение расчетных усилий, нормативных и расчетных характеристик бетона и арматуры

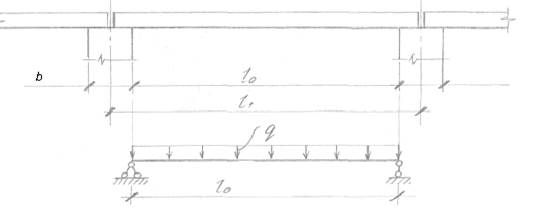
Рис. 2.1 Расчётная схема плиты.

Расчетный пролет плиты:

ℓ₀ = ℓ₁  - b_р /2 = 5600 – 250/2 = 5475 мм.

Задаёмся  b_р = 250 мм.

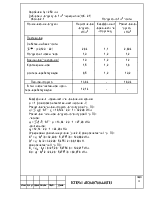
Собираем нагрузку на 1 м²  перекрытия (таб. 2.1)

Таблица 2.1                                                                                 Нагрузка на 1 м²  плиты

Коэффициент  надежности по назначению здания:

γ_п = 1 (для класса ответственности здания - I)

Расчетная погонная нагрузка на плиту для I гр.  ПС:

q = (∑q_м²) · BF' · γ_п = 16,104 · 2,0 · 1 = 32,208 кН/м

Расчетная   погонная нагрузка на плиту для II гр.  ПС:

-полная:

q_п =(∑qⁿ _м²) · BF' · γ_п = 13,64 · 2,0 · 1 = 27,28 кН/м

-длительная:

q_ℓ = 12,14 · 2,0 · 1 = 24,28 кН/м

Определяем расчетные усилия  (рис 2.4) для расчетов по I гр.  ПС:

M¹  = q · ℓ₀² /8 =32,208 ·  5,475² / 8 = 120,682 кНм.

Q¹ = q · ℓ₀ /2 = 32,208 · 5,475 / 2 = 88,169 кН.

для расчетов по II гр.  ПС:

M_п = q_tot ·  ℓ₀² / 8 =27,28 · 5,475²/ 8 = 102,217 кНм.

М_ℓ = q_ℓ  · ℓ₀² /2 =24,28 · 5,475² / 8 = 90,976  кНм.

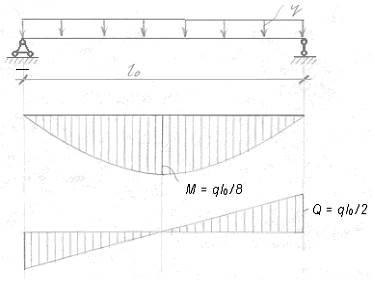
Рис. 2.2 Расчётные усилия в плите.

Определим нормативные  и расчетные характеристики бетона и арматуры.

Так как класс бетона В25, то корректируем его. Принимаем бетон В30.

γ_в2  = 0,9.

R_вn = R_{в, ser} = 22,0 МПа [3]   табл. 1

R_вtn = R_вt,ser = 1,8 МПа   [3]  табл. 1

R_в = R_в ·  γ_в2 = 15,3 МПа  [3] табл. 2

R_вt  = R_вt ·  γ_в2 = = 1,08 МПа  [3]  таб. 2

Е_в = 26000 МПа   [3]  таб. 4

Для предварительно напрягаемой арматуры касса А - 1000:

R_s =815 МПа [2]  табл. 8

R_sn = R_{s, ser} = 980 МПа [3] табл. 7

E_s = 190000 МПа [3] п.2.2.2.6

2.1 Расчет плиты no предельным состояниям I группы

Расчет прочности нормальных сечений на действие изгибающего момента.

b = b_f^’ – n· 159 = 1960 – 10· 159 = 370 мм.

Проверяем условие: М¹ ≤ М_п = γ_в2 ·  R_b ·  b_f^’ · h _f^’ ·  ( h₀ - h _f^’/2)

h₀ = h-a = 220-30 =190 мм.

М_п = 15,3 · 10³ ·  1,96 ·  0,031 ·  (0,19 – 0,031/2) = 162,22 кНм.

М¹ = 120,68 кНм ≤ М_п = 162,22 кНм.

Условие выполняется, следовательно, х < h _f^’,то есть нейтральная ось проходит через полку, рассчитываем сечение как прямоугольное.

α_m =М¹ / (γ_в2 ·  R_b ·  b_f^’ ·  h ₀²) =120,68 / (15300·  1,96· (0,19 м)²) =0,111

ξ = 1 - √(1 - 2 α_m) = 0, 118 < ξ_R= 0,386

ξ_R=0,8 / ( 1+ ε_s,el / ε_{b, ubt} )

ε_{b, ubt} – относительные деформации сжатого бетона при напряжениях, равных R_b, принимаем 0,0035.

ε_s,el – относительные деформации арматуры растянутой зоны, вызванные внешней нагрузкой при достижении  в этой арматуре напряжений, равных R_s, находим по формуле:

ε_s,el = (R_s +400 – σ_sp^’)/E_s, где σ_sp^’- величина преднапряжения арматуры с учётом всех потерь.

В расчётах принимаем σ_sp^’= σ_sp – 100 МПа.

σ_sp ≤ 0,8 ·  R_sn = 0,8 _* 980= 784 МПа. Величина преднапряжения должна быть не менее 0,3 _* R_sn = 294 МПа.  Принимаем σ_sp =600 МПа.

Тогда σ_sp^’= 600 – 100 = 500 МПа.

ε_s,el = (815 +400 – 500)/190000 =0,00376

ξ_R=0,8 / (1+ 0,00376 / 0,0035) = 0,386

η =1 – ξ /2 =0,941

A_sр = (γ_в2 ·  R_b ·  b_f^’ ·  h ₀ ·  ξ) / (R_s ·  γ_s3)

Так как ξ < ξ_R , то  γ_s3 = 1,85 – 0,25 ·  ξ / ξ_R =1,85 – 0,25 · 0,111/0,386= 1,778 ≥ 1,15, следовательно, принимаем γ_s3 = 1,15.

A_sр = 120,68/ (815000·  1,15 _* 0,941 _* 0,19) = 720 · 10^{-6 м2}.

Принимаем 5 стержней ø 14 мм (A_sр = 769мм² ).

Расчет прочности наклонных сечений.

Проверяем условия: 

Q_max ≤ 2,5 R_вt *b* h₀

Q_max = 88,17 кН < 2,5* 1080* 0, 370* 0,19 =189,81 кН

Упрощённо принимаем Q_b1 = Q_bmin , а с=2* h₀= 0,475 м.

Усилие обжатия от растянутой продольной арматуры:

Р= 0,7* σ_sp* A_sр =0,7* 600* 0,769 = 322,98 кН.

φ_n = 0,1*Р / R_вt *b* h₀ = 0,1*322,98 / 1080 *0,370* 0,19=0,425 < 0,5. φ_в3 = 0,4.

Q_bmin = φ_{в3 *} ( 1+ φ_n)* R_вt *b* h₀ = 0,4 _* ( 1+ 0,425)* 1080 *0,37* 0,19 = 43,28 кН.

Так как Q = Q_max - q · с = 88,17 – 32,21 · 0,475 = 72,87 кН ≥ Q_bmin = 43,28 кН, то для прочности наклонных сечений требуется поперечная арматура.

Q_sw = Q - Q_bmin = 29,59 кН.

Поперечные стержни изготавливаются из арматуры В-500 ø 4.

q_sw = Q_sw/ h₀ =155,74 кН/м.

A_sw = s₁ ∙ q_sw / R_sw = 0,1 ∙ 155,74 / 365000 = 42,67 мм².

Принимаем 6 каркасов из арматуры В-500 ø 4 с шагом