Согласно [2] , пустотная плита, эксплуатируемая в закрытом помещении и армированная напрягаемой арматурой класса А800 диаметром 10 мм, должна удовлетворять 3-ей категории трещиностойкости, т.е. допускается непродолжительнае раскрытие трещин шириной [аcrc 1] = 0,3 мм и продолжительное - [аcrc 2] = 0,2 мм.
Прогиб плиты от действий постоянной и длительной нагрузок не должен превышать fu = 27,375 мм.
Приведенное сечение
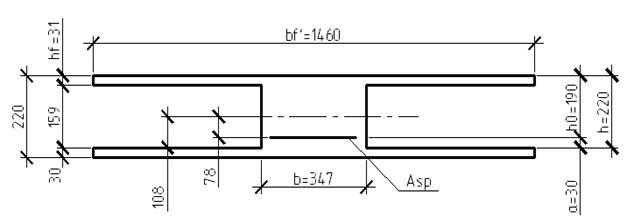
Рис.2.7
Геометрические характеристики приведенного сечения (рис. 2.7)
Аred =1817 см2
y0= 10,8 см
Ired =107486 см2
Wred inf = 9923 см3
Wred sup = 9624 см3
Определяем первые потери предварительного напряжения арматуры
-Потери от релаксации напряжений в арматуре:
∆σ1 = 0,1×σsp×20= 0,1×680×20 = 48 МПа
-Потери от температурного перепада:
∆σ2 =1,25×∆t =1,25×65 = 81,25 МПа
-Потери от деформации стальной формы
∆σ3 =0
-Потери от деформации анкеров виде инвентарных зажимов:
∆σ4 = (∆ℓ/ℓ)×Es =(0,002/6,6)×2×105 = 60,61MПа, где ∆l=2 мм
l- длина натягиваемого стержня
∆σsp(1)=∆σ1+∆σ2+∆σ3+∆σ4=48+81,25+0+60,61=189,96 мПа
-Потери от усадки бетона:
∆σ5=εb,sh×Es=0,0002×2×105=40 мПа
-Потери от быстронатекающей ползучести бетона:
Вычислим напряжения в бетоне в середине пролета от действия силы PI
PI = (σsp –∆σsp(1))×Asp=0,393(680-189,86)=192,6 кН
Точка приложения усилия PI совпадает с центром тяжести сечения напрягаемой арматуры, поэтому
еор =у0 - а = 108-30 = 78 мм
Напряжение σвр на уровне растянутой арматуры (то есть при у = еор =78,2 мм):
σвp = PI /Ared +PI ×е2ор/Yred=0,193/0,1817+0,193×0,0782/0,001075=2,15 мПа
∆σ6=(0,8×α ×φb,cr ×σbp)/(1+α×μsp(1+I2s×Ared /Yred)+(1+0,8×φb,cr ))=22,18 мПа
μsp=Asp/А=393/144233=0,002724
∆σsp(2)=∆σsp(1)+∆σ5+∆σ6=189,86+40+22,18=252,04 мПа
Передаточная прочность бетона Rвр назначается из условий:
Rвр ≥ 50% от класса бетона
Rвр≥ 15 МПа
Rвр >30/2 = 15 МПа ≥15 МПа
Принимаем, Rвр = 15 МПа, тогда
Проверка образования трещин в плите
M≤Mcrc
Mcrc = Rвt,ser ×Wpl inf+P(2) ×(eop+r) = 1750×0,014855+168(0,078+0,0546) = 48,32 кНм.
P(2)=Asp( σsp-∆σsp(2) )=0,393(680-252,04)=168 кН
r=Wred /Ared=9923/1817=5,46 см
Так как Мr =26,93 кНм ≤ Мcrc =48,32 кНм , то трещины в нижней растянутой зоне не образуются, следовательно расчет по раскрытию трещин не требуется.
Расчет прогиба плиты
Расчет выполняем согласно [3] от действия постоянной и длительной нагрузок (М = Мℓ = 21,31 кНм)
Кривизна от продолжительного действия постоянной и длительной нагрузок формула :
(1/r)2 =M/(Ев1 ×Ired )=21,31/(9,848 ×106 ×107486 ×10-8)=0,002м
Eb1 =Eb|(1+φb,cr ) 32,5 ×103/(1+2,3)=9,848×103 мПа,
где φb,cr=2,3 табл 5 [3]
f=5×l2×(1/r)2 /48=5×5,4752×0,002/48=0,0062 мм=6,24мм≤fult=l/200=27,375мм –удовлетворяет требования по деформации.
Нагрузка на ригель
Назначаем предварительные размеры поперечного сечения ригеля :
высота сечения h=(1/10…1/15)ℓ2 = (1/13)×6400 = 492 мм, принимаем 550мм
ширина сечения в =(0,3...0,5) h = 0,4×550 = 220 мм, принимаем 200 мм
Расчетная нагрузка на 1 м длины ригеля :
q = (g + ν)×ℓ1×γn + h×в×ρ×γf×γn, где
g = 3,5868 кН/м2 - постоянная расчетная нагрузка от конструкции пола и плит перекрытия (таб. 2. 1)
ν = 4,8 кН/м - временная расчетная нагрузка на 1м2 (таб. 2.1)
ℓ1= 5,6 м - шаг колонн в продольном направлении
ρ = 25 кН/м3 - плотность железобетона
q= (8,3868)×5,6×1+0,55×0,2×25×1,1×1=50,99 кH/м-полная расчетная погонная нагрузка на ригель
g=(3,5868)×5,6×1+0,55×0,2×25×1,1×1=50,99 кH/м- постоянная расчетная погонная нагрузка
Армирование плиты с круглыми пустотами см. графическую часть лист 2.
2.2 Расчет неразрезного ригеля
Предварительные размеры поперечного сечения ригеля были назначены в п. 2.1.4. Поэтому окончательно принимаем
в=200 мм; h=550 мм.
Полная расчетная нагрузка на 1 м длины ригеля :
q =50,99 кH/м
Ординаты сгибающих эпюр М и Q см. распечатку ЭВМ.
2.2.1 Характеристики бетона и арматуры для ригеля.
Для тяжёлого бетона класса В30 при влажности 70 %
Rв = Rв снип× γв1 = 17×0,9 =15,3 МПа [2] таб. 13
Rвt =Rвt снип ×γв2 = 1,15×0,9 =1,035 МПа [2] таб. 13
Для продольной рабочей арматуры класса А300
Rs =270 МПа [2] таб. 22
2.2.2 Расчет прочности ригеля по сечениям, нормальным к продольной оси.
Принимаем схему армирования с расположением надопорной арматуры в ригеле в один ряд.
Сечение в пролете
Мmax = 191,8 кНм (см. графическую часть лист 3)
h0= h–a = 550 - 60=490 мм
Подбор продольной арматуры производим согласно п. 3.18 [6] :
αm = Мmax /(Rв×в×h02)=191,8×106/ (15,3×200×4902) =0,261
ξ = 1 - √(1 - 2 αm) = 1 - √(1 – 2×0,261) =0,31 < ξR =0,57
Так как ξ =0,208 < ξR =0,583, mo требуемая площадь растянутой арматуры :
As = Rb×в×ξ×h0 /Rs=15,3×200×0,31×0,49/270= 1721,53 мм2
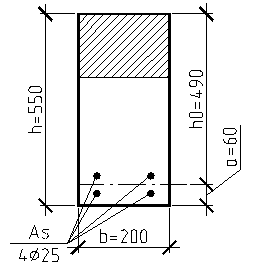
Принимаем 4 Ǿ 25 А300 с Аs = 1256 мм2.
Сечение на опоре :
Мmax = 130,4 кНм (см. графическую часть лист 3)
h0= h – a = 550 - 40=510 мм
αm = Мmax /(Rв×в×h02)=130,4×106/ (15,3×200×5102) =0,164
ξ = 1 - √(1 - 2 αm) = 1 - √(1 – 2×0,164) =0,18 < ξR =0,57
Так как ξ =0,208 < ξR =0,583, mo требуемая площадь растянутой арматуры :
As = Rb×в×ξ×h0 /Rs=15,3×200×0,18×0,51/270= 1040,4 мм2
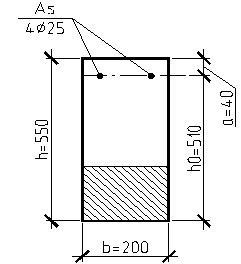
Принимаем 2 Ǿ 28 А300 с Аs =1232 мм2.
2.2.3 Расчет ригеля по сечениям, наклонным к продольной оси.
Qmax = 176,3 кН –перерезывающие усилие на приопорном участке
Если Qb1 <2Mb /h0 –Qmax => qsw=(Qmax-Qb1 )/1,5h0 ,
где Qb1=2√Mb×q1 -поперечная сила в нормальном сечении от внешней нагрузки
Mb=1,5×Rbt×b×h02=1,5×1,15×0,2×0,492=82,83 кНм- момент воспринимаемый бетоном
q1 =q-0,5qv=50,99-0,5×4,8×5,6×1=37,55 кн/м
Qb1=111,01 кН
Qb1 =111,01<2Mb /h0 –Qmax=2×82,83/0,49-176,3=161,78=>
qsw=(176,3-111,01)/(1,5×0,49)=88,83 кН/м
т.к. qsw=88,83>0,25×Rbt×b=57,5 –следовательно корректировка значения интенсивности армирования не требуется
Задаемся шагом поперечной арматуры:
S1 ≤1/2h0
S1 ≤300 ,из двух условий принимаем наименьшее с кратностью 10мм
S1=190мм
S2 ≤3/4h0
S2 ≤500 ,из двух условий принимаем наименьшее с кратностью 50мм
S2=300мм
Smax=Rbt×b×h02/Qmax=0,395 м=395 мм- максимально допустимый
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.