Расчет режимов местных электрических сетей, страница 2

          Рассмотрим процесс расчета местной электрической сети на примере неразветвленной сети, заданной  на рис. 6.14,а. В соответствии с первым допущением ее схема замещения  приведена на рис. 6.14,б. При этом нагрузки узлов в ней заданы мощностями.

          При расчете распределения мощностей в ней воспользуемся пятым допущением. Так как мощность по всей длине каждого участка одинакова, то мощность в линии 34 .

          Мощность на участке 23  находят по первому закону Кирхгофа для

узла 3

          Аналогично мощность в линии 12

                                                                                  (6.64)

          Таким образом, мощность, передаваемая по любому участку сети, определяется простым суммированием мощностей нагрузок, получающих питание по этому участку.

          Перейдем к расчету напряжений, при этом используем четвертое допущение. В рассматриваемой сети наибольшее значение потеря напряжения имеет от точки 1 до точки 4. Ее можно записать в виде суммы потерь напряжения  на каждом участке

          При найденных мощностях на участках наибольшую потерю напряжения можно найти через них и сопротивления участков по формуле

                                      (6.65)

          Для сети с n узлами нагрузки и известными мощностями  и сопротивлениями  участков потеря напряжения до точки n равна

                                                                                (6.66)

Для расчета наибольшей потери напряжения  по формуле (6.66) необходимо предварительно по выражениям аналогичным (6.64) найти мощность на каждом участке. Это  исключает другой способ определения наибольшей потери напряжения.

Выразим в формуле (6.65) потоки мощности участков линии через мощности узлов нагрузки (см. формулу (6.64))

 

Раскроем это выражение

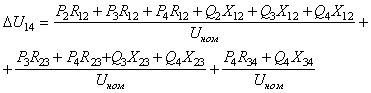                                            (6.67)      

Введем обозначения

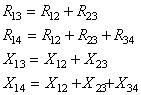                                                                                              (6.68)

          Преобразуем формулу (6.67), используя выражения  (6.68) к следующему виду

          В итоге для сети с n нагрузками получим выражение

                                                   ,                             (6.69)

где  - мощность i-го узла нагрузки;

       ;  - сопротивление от точки 1 до i-го узла.

          В отличии от формулы (6.66) здесь расчет потери напряжения производится не по мощности в линии, а по мощности узлов нагрузки, что иногда проще.

Рассмотрим некоторые частные случаи.

          Как отмечалось, в соответствии со вторым допущением в некоторых случаях для кабельной линии можно пренебречь индуктивным сопротивлением. Тогда формулы (6.66) и (6.69) упрощаются и примут соответственно вид

                                                                                              (6.70)

                                                                                               (6.71)

          Если сечения проводников и конструктивное исполнение всех участков линии одинаковы, то общие формулы (6.66) и (6.69) расчета наибольшей потери напряжения также становятся более простыми

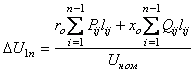                                                                                   (6.72)

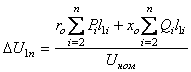                                                                                   (6.73)

          Рассмотрим расчет режима местной электрической сети, когда нагрузки заданы не  мощностями, а токами (рис.6.14,в).

          Обычно это имеет место в сетях напряжением до 1 кВ. В таких случаях нагрузка представляется полным током  и коэффициентом мощности cos , по которым при необходимости можно найти активную  и реактивную составляющие тока нагрузки

                                                                                                           (6.74)

          По ним можно найти  соответственно активную и реактивную мощность нагрузки

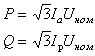                                                                                                        (6.75)

          Подставив в формулу (6.69) мощности узлов нагрузки, выраженные в виде (6.75) и преобразовав ее, получим

                                                                                   (6.76)

                С учетом (6.74) можно получить другой вид формулы (6.76)

                                                                      (6.77)

          По аналогии с формулой (6.66) нетрудно получить выражение , где

расчет наибольшей потери напряжения ведется по токам  в линии

                                                                    (6.78)

          Расчет потери напряжения по формулам (6.77) и (6.78) упрощается,

если в узлах нагрузки подключены однотипные потребители с одинаковым

коэффициентом мощности

                                                                    (6.79)

                                                                  (6.80)

          Большинство местных электрических сетей, особенно воздушных,  

выполняется разветвленными (рис.6.15). В них мощности или токи на

отдельных участках находят простым суммированием нагрузок узлов, как и в

неразветвленной сети. Наибольшая потеря напряжения здесь может быть

либо на участке 13, либо на участке 15.

          Так как участок 12 у них общий, то, если  <  , то наибольшая

потеря напряжения имеет место до точки 5.

По формуле (6.69)

          Здесь нагрузка узла 3, которая передастся по участку линии 12, условно

переносится в узел 2, принадлежащий рассматриваемому участку сети 15.